7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 37)

Biểu diễn miền nghiệm của của bất phương trình hai ẩn 2x − y ≥ 0.

Cho phương trình 5sin 2x + sin x + cos x + 6 = 0. Trong các phương trình sau, phương trình nào tương đương với phương trình đã cho?

Chứng minh phương trình sau đây vô nghiệm:

5sin 2x + sin x + cos x + 6 = 0.

Phân tích đa thức sau thành nhân tử:(b − 2c)(a − b) − (a + b)(2c − b).

Cho a, b, c là các số dương tùy ý. Chứng minh rằng:

\[\frac{{bc}}{{b + c + 2a}} + \frac{{ca}}{{c + a + 2b}} + \frac{{ab}}{{a + b + 2c}} \le \frac{{a + b + c}}{4}\].

Cho góc aÎ (90°; 180°). Khẳng định nào sau đây đúng?

Cho a là góc tù. Mệnh đề nào đúng trong các mệnh đề sau?

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a; cạnh bên SA vuông góc với mặt đáy, \(SA = a\sqrt 3 \); gọi M là trung điểm AC. Tính khoảng cách từ M đến mp(SBC).

Cho hình chóp S.ABC, đáy ABC đều cạnh 2a. Cạnh bên SA vuông góc với mặt đáy. Góc giữa SB và (ABC) là 60°. Tính thể tích S.ABC.

Chứng minh tổng 3 góc tam giác bằng 180 độ.

Gọi M = cos x + cos 2x + cos 3x thì:

Biến đổi tích thành tổng: cos x.cos 2x.cos 3x.

Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = \frac{{2x - 1}}{{x + 1}}\) trên đoạn [0; 3]. Tính hiệu M − m.

Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = \frac{{2x + 1}}{{x - 1}}\) trên đoạn [2; 4]. Giá trị của tổng M + m bằng.

Tính S là tổng tất cả các nghiệm của phương trình 4(2^2x + 2^−2x) − 4(2^x + 2^−x) − 7 = 0.

Gọi S là tổng các giá trị nguyên của tham số m để phương trình 4^x + 7 = 2^{x + 3} + m² + 6m có nghiệm x Π(1; 3). Chọn đáp án đúng.

Phương trình 2^{2x + 1} = 32 có nghiệm là:

Bất phương trình \[\frac{{2 - x}}{{2x + 1}} \ge 0\] có tập nghiệm là:

Tìm số a để:

a) Đa thức x³ + 3x² + 5x + a chia hết cho x + 3

b) Đa thức x³ − 3x + a chia hết cho đa thức x² − 2x + 1

Tìm a để đa thức x³ + 3x² + 5x + a chia hết cho đa thức x + 3

Biểu diễn vectơ \(\overrightarrow a \) dưới dạng: \(\overrightarrow a = x\,.\,\overrightarrow i + y\,.\,\overrightarrow j \) biết

a) \(\overrightarrow a \left( {1;\; - 1} \right)\)

b) \(\overrightarrow a \left( {3;\;5} \right)\)

c) \(\overrightarrow a \left( {6;\;0} \right)\)

d) \(\overrightarrow a \left( {0;\; - 2} \right)\)

Xác định tọa độ của vectơ \(\overrightarrow a \) biết:

a) \(\overrightarrow a = 3\overrightarrow i - 4\overrightarrow j \)

b) \(\overrightarrow a = - 2\overrightarrow i + \frac{2}{3}\overrightarrow j \)

c) \(\overrightarrow a = - 4\overrightarrow j \)

d) \(\overrightarrow a = - 7\overrightarrow i \)

Gọi M là tập hợp các số tự nhiên gồm 9 chữ số khác nhau. Chọn ngẫu nhiên một số từ M, tính xác suất để số được chọn có đúng 4 chữ số lẻ và chữ số 0 đứng giữa hai chữ số lẻ (các chữ số liền trước và liền sau của chữ số 0 là các chữ số lẻ)

Chọn ngẫu nhiên một số có 4 chữ số. Gọi P là xác suất để tổng các chữ số của số đó là một số lẻ. Khi đó P bằng

Tìm x, biết: \(\frac{{2x - 1}}{3} = \frac{{2 - x}}{{ - 2}}\).

Tìm x, biết: \(\frac{2}{x} - \frac{1}{3} = \frac{2}{5}\)

Tìm x, biết: 2.3^x = 10.3¹² + 8.27⁴.

Phân tích đa thức sau thành nhân tử:

a) 4x² + y² − 4xy

b) 27 + 9x² + 27x + x³

c) 8z³ + 1

d) (2z − 3)² − 16

e) (2x − 7)² − (x + 2)²

Phân tích các đa thức sau thành nhân tử

a) 4x² − 4xy + y²

b) 9x³ − 9x²y − 4x + 4y

c) x³ + 2 + 3(x³ − 2)

Cho hàm số y = f (x). Hàm số y = f ¢(x) có bảng biến thiên như sau:

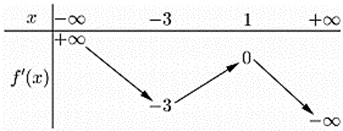
Bất phương trình f (x) < e^x + m đúng với mọi x Î (−1; 1) khi và chỉ khi:

Với hai điểm phân biệt A, B cố định và phân biệt. Một đường thẳng l thay đổi luôn đi qua A và cách B một khoảng \(\frac{{AB}}{2}\). Gọi H là hình chiếu của B lên l. Tập hợp điểm H là

Cho một điểm A cố định và một đường thẳng a cố định không đi qua A. Gọi O là một điểm thay đổi trên a. Chứng minh rằng các mặt cầu tâm O bán kính r = OA luôn luôn đi qua một đường tròn cố định.

Cho hàm số f (x) có đạo hàm trên khoảng (a; b). Trong các mệnh đề sau, mệnh đề nào sai?

Cho hàm số y = f (x) có đạo hàm trên (a; b). Phát biểu nào sau đây sai?

Cho hàm số \(y = \frac{x}{2} + \cos x\). Mệnh đề nào sau đây đúng?

Cho hàm số y = e^{cos x}. Mệnh đề nào sau đây đúng?

Cho hàm số y = f (x) xác định và có đạo hàm trên K. Khẳng định nào sau đây là sai?

Cho K là một khoảng và hàm số y = f (x) có đạo hàm trên K. Khẳng định nào sau đây là sai?

Cho tam giác ABC có G là trọng tâm. Diện tích của các tam giác AGB, BGC và AGC có bằng nhau hay không?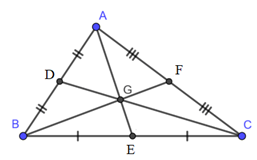

Cho tam giác ABC, điểm G nằm trong tam giác sao cho S_AGB= S_AGC = S_BGC. Chứng minh G là trọng tâm của tam giác ABC.

Tính giá trị lớn nhất của hàm số y = −x⁴ + 3x² + 1 trên [0; 2].

Giá trị lớn nhất và nhỏ nhất của hàm số y = x⁴ + 2x² − 1 trên [−1; 2] lần ượt là M, m. Tính giá trị của tích M.m.

Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số \(y = \left| {\frac{1}{4}{x^4} - \frac{{19}}{2}{x^2} + 30x + m - 20} \right|\) trên đoạn [0;2] không vượt quá 20. Tổng các phần tử của S bằng

Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số \(y = \left| {\frac{1}{4}{x^4} - 14{x^2} + 48x + m - 30} \right|\) trên đoạn [0;2] không vượt quá 30. Tính tổng các phần tử của S.

Hình đa diện sau có bao nhiêu mặt?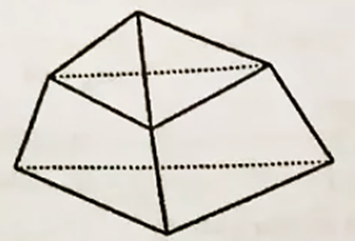

Hình đa diện sau có bao nhiêu mặt?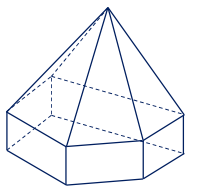

Làm tính nhân:

a) 3x.(5x² − 2x − 1);

b) (x² + 2xy − 3).(− xy);

c) \(\frac{1}{2}{x^2}y\,.\,\left( {2{x^3} - \frac{2}{5}x{y^2} - 1} \right)\).

Làm tính nhân: 3x.(5x² − 2x − 1)

Phân tích các đa thức sau thành nhân tử:

a) (x + y)² − (x − y)²

b) x² − 2x − 4y² − 4y

c) x²(x − 1) + 16(1 − x)

Rút gọn biểu thức:

a) (x + y)² + (x − y)²

b) (x + y)² − (x − y)²

c) (x + 2)² − 2(x + 2)(x − 3) + (x − 3)²

Cho ab + bc + ca = 1. Khi đó (a² + 1)(b² + 1)(c² + 1) bằng

Cho a; b; c đôi một khác nhau. Tính giá trị biểu thức:

\(P = \frac{{{a^2}}}{{\left( {a - b} \right)\left( {a - c} \right)}} + \frac{{{b^2}}}{{\left( {b - c} \right)\left( {b - a} \right)}} + \frac{{{c^2}}}{{\left( {c - b} \right)\left( {c - a} \right)}}\).

Tính tổng tất cả các nghiệm của phương trình 3^2x − 2.3^{x + 2} + 27 = 0.

Tìm các nghiệm của phương trình \[\frac{{{3^{2x - 6}}}}{{27}} = {\left( {\frac{1}{3}} \right)^x}\].

Tìm giá trị của tham số m để hàm số \[y = \frac{{ - mx - 5m + 4}}{{x + m}}\] nghịch biến trên từng khoảng xác định.

Cho hàm số \[y = \frac{{mx - 5m - 4}}{{x + m}}\] (m là tham số thực). Có bao nhiêu nghiệm nguyên của m để hàm số đã cho nghịch biến trên từng khoảng xác định?

Điều tra thời gian hoàn thành một sản phẩm của 20 công nhân, người ta thu được mẫu số liệu sau (thời gian tính bằng phút).

Kích thước mẫu là bao nhiêu?

Điều tra thời gian hoàn thành một sản phẩm của 20 công nhân, người ta thu được mẫu số liệu sau (thời gian tính bằng phút).

Có bao nhiêu giá trị khác nhau trong mẫu số liệu trên?

Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C, AC = 3a và SA vuông góc với mặt phẳng đáy. Tính khoảng cách từ B đến mặt phẳng (SAC).

Cho hình chóp S.ABC có đáy là tam giác vuông tại C, \[AC = a;\;BC = \sqrt 2 a\], SA vuông góc với mặt phẳng đáy và SA = a. Góc giữa đường thẳng SB và mặt phẳng đáy bằng

Cho khối chóp đều S.ABCD có tất cả các cạnh đều bằng \(a\sqrt 3 \). Tính thể tích V của khối cầu ngoại tiếp hình chóp.

Cho hình chóp đều S.ABCD có tất cả các cạnh bằng nhau và bằng a. Tính thể tích V khối cầu ngoại tiếp hình chóp S.ABCD.

Cho tam giác ABC vuông cân tại A, tia phân giác của góc B và góc C cắt AC và AB lần lượt tại E và D.

a) Chứng minh BE = CD, AD = AE.

b) Gọi I là giao điểm của BE và CD, AI cắt BC tại M. Chứng minh tam giác MAC vuông cân.

c) Từ A và D vẽ các đường thẳng vuông góc với BE. Các đường này cắt BC tại K và H. Chứng minh HK = KC.

Tính đạo hàm của hàm số y = 2^x.

Tính đạo hàm \(\frac{1}{x}\).

Cho biểu thức: \(N = \frac{{2x - 10}}{{{x^2} - 7x + 10}} - \frac{{2x}}{{{x^2} - 4}} + \frac{1}{{2 - x}}\).

a) Rút gọn N.

b) Tìm giá trị nguyên của x để N nhận giá trị nguyên.

Cho \(N = \frac{{2x - 10}}{{{x^2} - 7x + 10}} - \frac{{2x}}{{{x^2} - 4}} + \frac{1}{{2 - x}}\). Tìm giá trị của x để N có giá trị xác định.

Phân tích đa thức 4x² − 5x + 1 thành nhân tử.

Phân tích đa thức thành nhân tử:

a) 4x² + 5x − 9

b) 4x³ + 4x² − 5x − 3

Tìm số nguyên dương n sao cho:

\({\log _{2018}}2019 + {2^2}{\log _{\sqrt {2018} }}2019 + {3^2}{\log _{\sqrt[3]{{2018}}}}2019 + ... + {n^2}{\log _{\sqrt[n]{{2018}}}}2019\)

= 1010².2021²log ₂₀₁₈ 2019

Cho n là số nguyên dương, tìm n sao cho:

\[{\log _a}2019 + {2^2}{\log _{\sqrt a }}2019 + {3^2}{\log _{\sqrt[3]{a}}}2019 + ... + {n^2}{\log _{\sqrt[n]{a}}}2019 = {1008^2}\,.\,{2017^2}{\log _a}2019\]

Tập hợp tất cả các giá trị của tham số m để hàm số \(y = \frac{{3x + 5}}{{{{\log }_{2018}}\left( {{x^2} - 2x + {m^2} - 4m + 5} \right)}}\) xác định với mọi x Î ℝ là:

Tìm tập hợp tất cả các giá trị của tham số m để hàm số \(y = \frac{{4x + 7}}{{{{\log }_{2018}}\left( {{x^2} - 2x + {m^2} - 6m + 10} \right)}}\) xác định với mọi x Î ℝ.

Chứng minh x² + y² ³ 2xy.

Chứng minh đẳng thức: x² + y² = (x + y)² − 2xy.

Rút gọn: \[F = \sqrt {3 + \sqrt 5 } + \sqrt {7 - 3\sqrt 5 } - \sqrt 2 \].

Chứng minh các đẳng thức sau:

a) \(\left( {\frac{{2\sqrt 3 - \sqrt 6 }}{{\sqrt 8 - 2}} - \frac{{\sqrt {216} }}{3}} \right)\,\,.\,\frac{1}{{\sqrt 6 }} = - 1,5\)

b) \(\left( {\frac{{\sqrt {14} - \sqrt 7 }}{{1 - \sqrt 2 }} + \frac{{\sqrt {15} - \sqrt 5 }}{{1 - \sqrt 3 }}} \right):\frac{1}{{\sqrt 7 - \sqrt 5 }} = - 2\)

c) \[\frac{{a\sqrt b + b\sqrt a }}{{\sqrt {ab} }}:\frac{1}{{\sqrt a - \sqrt b }} = a - b\] với a, b dương và a ¹ b

d) \[\left( {1 + \frac{{a + \sqrt a }}{{\sqrt a + 1}}} \right)\left( {1 - \frac{{a - \sqrt a }}{{\sqrt a - 1}}} \right) = 1 - a\] với a ³ 0; a ¹ 0

Tìm x biết: 3^{x + 1} = 9^x

Tìm nghiệm của phương trình 3^{x − 1} = 9.

Tính b, c biết \(\frac{a}{b} = \frac{b}{c} = \frac{c}{a},\;a = 2005\) và a + b + c ¹ 0.

Cho a, b, c thỏa mãn điều kiện a.b.c = 2005. Chứng minh rằng biểu thức sau không phụ thuộc a, b, c:

\(A = \frac{{2005a}}{{ab + 2005a + 2005}} + \frac{{2005b}}{{bc + 2005b + 2005}} + \frac{c}{{ac + c + 1}}\)

Giải phương trình:\[\frac{{\cos x - \sqrt 3 \sin x}}{{2\sin x - 1}} = 0\].

Giải phương trình:\[\frac{{\sqrt 3 \sin x - \cos x}}{{2\sin x - 1}} = 0\].

Cho tam giác ABC. Chứng minh:

\(\tan \left( {\frac{A}{2}} \right)\tan \left( {\frac{B}{2}} \right) + \tan \left( {\frac{B}{2}} \right)\tan \left( {\frac{C}{2}} \right) + \tan \left( {\frac{C}{2}} \right)\tan \left( {\frac{A}{2}} \right) = 1\).

Cho tam giác ABC có số đo ba góc là A, B, C thỏa mãn điều kiện \(\tan \frac{A}{2} + \tan \frac{B}{2} + \tan \frac{C}{2} = \sqrt 3 \). Tam giác ABC là tam giác gì?

Tìm tập hợp các giá trị thực của tham số m để hàm số \(y = x + 1 + \frac{m}{{x - 2}}\) đồng biến trên mỗi khoảng xác định.

Tìm m để hàm số \(y = x + 2 + \frac{m}{{x - 1}}\) đồng biến trên mỗi khoảng xác định của nó.

Cho 4 điểm bất kì A, B, C, O. Đẳng thức nào sau đây đúng?

Cho 4 điểm bất kì A, B, C, O. Đẳng thức nào sau đây đúng?