7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 34)

Cho hình vuông ABCD cạnh bằng 2. Điểm M nằm trên đoạn thẳng AC sao cho \[{\rm{A}}M = \frac{{AC}}{4}\]. Gọi N là trung điểm của đoạn thẳng DC. Tính \(\overrightarrow {MB} .\overrightarrow {MN} \).

Cho hình vuông ABCD có cạnh bằng 2. Tính \(T = \left| {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {A{\rm{D}}} } \right|\).

Cho tam giác ABC cân tại A, O là trung điểm của BC. Vẽ đường tròn tâm O tiếp xúc với AB, AC tại H và K. Lấy E bất kỳ thuộc cung nhỏ HK. Vẽ tiếp tuyến tại E cắt AB, AC ở M, N.

a) Giả sử \(\widehat B = \widehat C = \alpha \). Tính \(\widehat {MON}\).

b) Chứng minh rằng OM, ON chia tứ giác BMNC thành ba tam giác đồng dạng.

c) Giả sử BC = 2a. Tính BM . CN.

d) MN ở vị trí nào thì tổng BM + CN nhỏ nhất?

Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm AB, K là điểm đối xứng với H qua điểm I.

a) Tứ giác ACHI là hình gì ? Vì sao?

b) Tứ giác AHBK là hình gì ? Vì sao?

c) Nếu tam giác ABC đều thì ACHI là hình gì?

d) Tam giác ABC có điều kiện gì thì AHBK là hình vuông.

Cho tam giác ABC vuông tại B (AB< AC) có AM là tia phân giác (M ∈ BC), trên cạnh AC lấy điểm N sao cho AB=AN.

a)Chứng minh ∆ABM = ∆ANM.

b) Chứng minh \(\widehat {BAC} = \widehat {CMN}\).

Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho \(\overrightarrow {BH} = \frac{1}{3}\overrightarrow {HC} \). Điểm M di động nằm trên BC sao cho \(\overrightarrow {BM} = x\overrightarrow {BC} \). Tìm x sao cho độ dài của \(\overrightarrow {MA} + \overrightarrow {GC} \) đạt giá trị nhỏ nhất.

Cho đa giác đều 20 đỉnh. Lấy ngẫu nhiên 3 đỉnh. Tính xác suất để 3 đỉnh đó là 3 đỉnh của một tam giác vuông không cân.

Cho đường tròn (O; R) và điểm A nằm ngoài (O). Từ A kẻ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC. Lấy D đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với (O) (E không trùng với D). Chọn câu đúng nhất:

Với các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số gồm 8 chữ số, trong đó chữ số 1 có mặt 3 lần, mỗi chữ số khác có mặt đúng 1 lần

Có bao nhiêu cách sắp xếp 3 nữ sinh, 3 nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ

Diện tích hình tam giác là 25,3 cm², chiều cao là 5,5 cm. Tính độ dài đáy của hình tam giác đó.

Tìm số có 3 chữ số abc sao cho \(\frac{{abc}}{{a + b + c}}\) lớn nhất.

Tìm số tự nhiên a, b biết ƯCLN(a, b) = 4 và a + b = 48.

Tính diện tích của 1 tam giác cân có chiều cao ứng với cạnh đáy bằng 10cm, chiều cao ứng với cạnh bên bằng 12cm.

Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).

a) Chứng minh rằng OA vuông góc với BC.

b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO.

c) Tính độ dài các cạnh của tam giác ABC, biết OB = 2cm và OA = 4cm.

Cho 3 đường thẳng: d₁: y= mx – m + 1; d₂: y = 2x + 3; d₃: y = x + 1.

a) Chứng minh rằng khi m thay đổi, đường thẳng d₁ luôn đi qua 1 điểm cố định.
b) Tìm m để 3 đường thẳng trên đồng quy. Tính tọa độ điểm giao nhau đó.

Cho đường thẳng d: y = 2x + 6 cắt Ox; Oy theo thứ tự A và B. Diện tích tam giác OAB là:

Tìm các số nguyên n sao cho 2n³ + n² + 7n + 1 chia hết cho 2n – 1.

Số nào khác tính chất với các số còn lại: 9678, 4572, 5261, 5133, 3527, 6895, 7768.

Cho tam giác ABC có AB = AC. Gọi D là trung điểm của BC. Kẻ DE vuông góc với AB; DF vuông góc với AC. Chứng minh: 

a) ∆DEB = ∆DFC;

b) ∆AED = ∆AFD;

c) AD là tia phân giác của \(\widehat {BAC}\).

Tìm x biết \(\left| {2{\rm{x}} - 3} \right| - \left| {3{\rm{x}} + 2} \right| = 0\).

Một khu vườn hình chữ nhật có diện tích 3600m² chiều rộng 40m, cửa ra vào của khu vườn rộng 5m. Người ta muốn làm hàng rào xung quanh vườn bằng 2 tầng dây thép gai. Hỏi cần phải dùng bao nhiêu mét thép gai để làm hàng rào?

Cho một hình chữ nhật và một hình thoi (như hình vẽ), đường chéo EK và FH của hình thoi lần lượt bằng chiều rộng, chiều dài của hình chữ nhật ABCD, biết hình chữ nhật ABCD có chiều dài gấp đôi chiều rộng và có diện tích bằng 32 m². Tính diện tích hình thoi EFKH.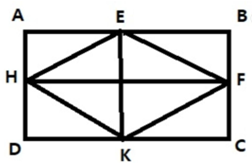

Trong các hình sau : hình vuông, hình bình hành, hình chữ nhật; hình thang cân. Những hình nào có hai đường chéo bằng nhau?

Tính diện tích tam giác vuông cân biết cạnh huyền 4 cm.

Tìm số nguyên x, biết: (–14 ) + x – 7 = –10.

Tìm x biết x² + 2 là bội của x + 2.

Tính nhanh :

a) 55 + 56 + 57 + 58 – 35 – 36 – 37 – 38.

b) (461 – 78 + 40) – (461 – 78 – 60).

c) –323 + 874 – (874 – 324 – 241).

Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi I là trung điểm của AB và D là điểm đối xứng của M qua I

a) Chứng minh AD song song BM và tứ giác ADBM là hình thoi.

b) Gọi E là giao điểm của AB và DC. Chứng minh AE = EM.

Tìm x biết \(\sqrt {3{\rm{x}} + 15} - \sqrt {4{\rm{x}} + 17} = \sqrt {x + 2} \).

Cho tứ diện ABCD. Gọi P, Q lần lượt là trung điểm của AB, CD. Điểm R nằm trên cạnh BC sao cho BR = 2RC. Gọi S là giao điểm của mp (PQR) và AD. Khi đó:

Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng \(R\sqrt 3 \). Hai điểm A, B lần lượt nằm trên hai đường trong đáy sao cho góc giữa AB và trục của hình trụ bằng 30°. Khoảng cách giữa AB và trục của hình trụ bằng:

Một người gửi ngân hàng 100 triệu đồng với kỳ hạn 3 tháng, lãi suất 2% một quý theo hình thức lãi kép. Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được sau 1 năm kể từ khi bắt đầu gửi tiền gần với kết quả nào sau đây:

Cho tam giác ABC vuông tại A có AB = 8 cm, AC = 6 cm, trung tuyến AM. Kẻ MD vuông góc với AB và Me vuông góc với AC.

a) Tứ giác ADME là hình gì? Vì sao?

b) Tìm điều kiện của tam giác ABC để tứ giác ADME là hình vuông.

c) Tính độ dài AM?

d) Tính diện tích tam giác ABM?

Cho tam giác ABC vuông tại A. Gọi D và E lần lượt là trung điểm của AB và BC.

a) Chứng minh tứ giác ACED là hình thang vuông.

b) Gọi F là điểm đối xứng của E qua D. Chứng minh ACEF là hình bình hành.

c) Chứng minh AEBF là hình thoi.

Từ các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau, chia hết cho 5 và chữ số 2 luôn có mặt đúng một lần?

Phương trình x – 12 = 6 – x có nghiệm là:

Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ.

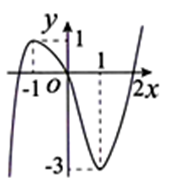Số nghiệm thực của phương trình f(2+f(e^x))=1là:

Cho đường tròn tâm O đường kính AB. Lấy điểm C thuộc đường tròn, với C không trùng A và B. Gọi I là trung điểm của AC. Vẽ tiếp tuyến của đường tròn tâm O tại tiếp điểm C cắt tia OI tại điểm D.

a) Chứng minh OI // BC.

b) Chứng minh DA là tiếp tuyến của đường tròn tâm O.

c)Vẽ CH ⊥AB (H ∈AB) và BK ⊥CD (K∈CD). Chứng minh CK² = HA.HB.

Chứng minh rằng n⁷–nchia hết cho 7, với mọi n là số nguyên.

Hỏi có bao nhiêu cách chọn ra hai số khác nhau trong các số tự nhiên từ 1 đến 20 sao cho tích của chúng chia hết cho 9?

Cho tam giác ABC vuông tại A, đường cao AH. Gọi I là trung điểm của AH. Chứng minh: \[{{\rm{a}}^2}\overrightarrow {IA} + {b^2}\overrightarrow {IB} + {c^2}\overrightarrow {IC} = \overrightarrow 0 \] với BC = a, AC = b và AB = c.

Cho hàm số \(y = \frac{{2{\rm{x}} - 1}}{{x + 1}}\) có đồ thị (C). Tìm tất cả các giá trị của tham số m để đường thẳng y = mx + 2 cắt (C) tại hai điểm phân biệt A, B sao cho tam giác OAB vuông tại O.

Trên mặt phẳng tọa độ Oxy cho A(1; –1), B(2; 1) và C(4; 5). Ba điểm A, B, C có thẳng hàng không?

Cho tam giác ABC có số đo 3 góc \(\widehat A,\widehat B,\widehat C\) lần lượt tỉ lệ với 1, 2, 3. Tính số đo các góc của tam giác ABC? Tam giác ABC là tam giác gì? Vì sao?

Một tam giác có chu vi bằng 36 cm cạnh của nó tỉ lệ với 3; 4; 5. Tính độ dài ba cạnh.