7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 32)

Cho định lí “Cho số tự nhiên n, nếu n⁵ chia hết cho 5 thì n chia hết cho 5”.

Định lí này được viết dưới dạng P Þ Q. Hãy phát biểu định lí đảo của định lí trên rồi dùng các thuật ngữ “điều kiện cần và đủ” phát biểu gộp cả 2 định lí thuận và đảo.

Viết các số (0,25)⁸ và (0,125)⁴ dưới dạng các lũy thừa với cơ số 0,5.

Cho một hộp đựng 4 viên bi đỏ, 5 viên bi xanh và 7 viên bi vàng. Lấy ngẫu nhiên một lần ba viên bi. Tính xác suất để trong ba viên bi lấy được chỉ có hai màu.

Một hộp đựng 7 viên bi xanh, 5 viên bi đỏ và 4 viên bi vàng. Có bao nhiêu cách lấy ra 8 viên bi có đủ 3 màu?

Tính hợp lý: (10² + 11² + 12²) : (13² + 14²).

Tìm nghiệm nguyên của phương trình: y²=x(x+1)(x+7)(x+8).

Đố bạn chỉ với 12 que diêm (hay 12 chiếc que có độ dài bằng nhau) mà xếp được thành 6 tam giác đều.

Cho n là số tự nhiên. Chứng minh: 5²ⁿ⁺¹ + 2ⁿ⁺⁴ +2ⁿ⁺¹ chia hết cho 23.

Với giá trị lớn nhất của a bằng bao nhiêu để phương trình:  asin²x + 2sin2x + 3acos²x = 2 có nghiệm

Cho biểu thức:

\[A = \left( {\frac{{x - 5\sqrt x }}{{x - 25}} - 1} \right):\left( {\frac{{25 - x}}{{x + 2\sqrt x - 15}} - \frac{{\sqrt x + 3}}{{\sqrt x + 5}} + \frac{{\sqrt x - 5}}{{\sqrt x - 3}}} \right)\]

a) Rút gọn A.

b) Tìm x để A < 1.

Cho tam giác ABC, \(\widehat A = {60^{\rm{o}}}\), AB + AC = 8cm. Tính giá trị lớn nhất của diện tích tam giác ABC.

Cho (O; R) và (O; R') tiếp xúc ngoài tại A. Kẻ dây cung AM của (O) và dây cung AN của (O') sao cho AM vuông góc với AN. Chứng minh:

a) OM song song O'N;

b) Xác định vị trí của AM và AN để diện tích tứ giác OMNO' lớn nhất.

Cho tứ diện S.ABC có đáy là tam giác đều ABC có đường cao AH = 2a. Gọi O là trung điểm AH, SO vuông góc mp(ABC) và SO = 2a. Gọi I là một điểm trên OH, đặt AI = x (a < x < 2a) và (α) là mặt phẳng qua I và (α) vuông góc AH.

a) Xác định thiết diện của (α) với tứ diện S.ABC.

b) Tính diện tích thiết diện của (α) và S.ABC theo a và x.

Cho tam giác ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.

Cho tam giác ABC có AM là trung tuyến. Gọi I là trung điểm AM và K là một điểm trên cạnh AC sao cho AK = 1/3 AC. Chứng minh ba điểm B, I, K thẳng hàng.

Cho tam giác ABC nhọn. Gọi M và N lần lượt là trung điểm của AB, BC.

a) Tính độ dài của MN biết AC = 16cm.

b) Gọi I là trung điểm của AC. Chứng minh tứ giác BMIN là hình bình hành.

c) Trên tia đối của tia NM lấy E sao cho N là trung điểm ME. Gọi K là giao điểm của EI và MC. Chứng minh MC = 3KC.

Cho tam giác ABC vuông cân tại A. Ở phía ngoài tam giác ABC, vẽ tam giác BCD vuông cân tại B. Tứ giác ABCD là hình gì? Vì sao?

Cho tam giác ABC vuông tại A, đường cao AH, M là trung điểm của BC, có BH = 4 cm, CH = 9 cm. Tính diện tích tam giác AHM?

Cho đường tròn (O), đường kính AB cố định, M là 1 điểm thuộc (O), (M khác A và B). Các tiếp tuyến của (O) tại A và M cắt nhau ở C. Đường tròn (I) đi qua M và tiếp xúc với đường thẳng AC tại C, CD là đường kính của (I). Chứng minh rằng:

a) 3 điểm O, M, D thẳng hàng.

b) Tam giác COD là tam giác cân.

c) Gọi N là giao điểm của OC và (I). Chứng minh khi M thay đổi thì đường thẳng qua N vuông góc với AB luôn đi qua điểm cố định.

Cho đường tròn (O), đường kính BC = 2R, điểm A nằm ngoài đường tròn sao cho tam giác ABC nhọn. Từ A kẻ 2 tiếp tuyến AM, AN với đường tròn (O). Gọi H là trực tâm của tam giác ABC, F là giao điểm của AH và BC. Chứng minh rằng:

a, 5 điểm A, O, M, N, F cùng nằm trên 1 đường tròn.

b, 3 điểm M, N, H thẳng hàng.

c, HA . HF = R² – OH².

Cho nửa hình tròn H như hình vẽ, đường kính hình tròn là 12cm.

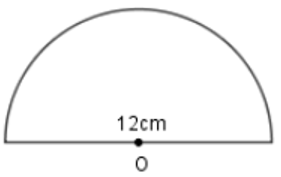
Chu vi hình H là:

Cho hai đường thẳng song song d₁, d₂. Trên đường thẳng d₁ lấy 10 điểm phân biệt, trên đường thẳng d₂ lấy 15 điểm phân biệt. Hỏi có bao nhiêu tam giác tạo thành mà ba đỉnh của nó được chọn từ 25 điểm vừa nói ở trên?

Có bao nhiêu số tự nhiên có 6 chữ số đôi một khác nhau trong đó chứa các chữ số 3, 4, 5 và chữ số 4 đứng cạnh chữ số 3 và chữ số 5?

Một kho gạo có 60 tấn gạo tẻ và gạo nếp trong đó số gạo nếp bằng \(\frac{3}{7}\) số gạo tẻ. Tính số gạo nếp, gạo tẻ có trong kho?

Lúc đầu, số sách ngăn một bằng \(\frac{2}{3}\) số sách ngăn hai. Sau khi lấy ra ở mỗi ngăn 10 quyển sách thì số sách ngăn một bằng \(\frac{3}{5}\) số sách ngăn hai. Hỏi lúc đầu, cả hai ngăn có bao nhiêu quyển sách?

Một tổ có 9 học sinh, trong đó có 5 học sinh nam và 4 học sinh nữ được xếp thành hàng dọc. Xác suất sao cho 5 học sinh nam đứng kề nhau là

Một cỗ bài có 52 quân, mỗi chất cơ, rô, nhép, bích đều có 13 quân. Có bao nhiêu cách lấy ra 5 quân sao cho có đủ cả 4 chất: cơ, rô, nhép, bích?

Tháng 2 năm nào đó có 5 ngày thứ Năm. Hỏi ngày 1 tháng đó là thứ mấy? Chủ nhật tháng đó vào những ngày nào?

Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n (n > 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n, biết rằng số tam giác có các đỉnh thuộc n + 6 điểm đã cho là 247.

Tìm giá trị lớn nhất của Q = \(\frac{1}{{x - 2\sqrt x + 3}}\).

Tìm giá trị của x để đa thức dư trong mỗi phép chia sau có giá trị bằng 0:

a) (3x⁵ – x⁴ – 2x³ + x² + 4x + 5) : (x² – 2x + 2);

b) (x⁵ + 2x⁴ + 3x² + x – 3) : (x² + 1).

Giải phương trình: \[{x^2}\; - 2\sqrt 3 x + 2 = 0\].

Tìm x, y, z nguyên dương thỏa mãn: xy + 1 chia hết cho z; yz + 1 chia hết cho x; xz + 1 chia hết cho y.

Xác định số hữu tỉ a sao cho: (x³ + ax² + 5x + 3) ⋮ (2x² + 2x + 3).

Tính: \(\frac{{{x^6} - {y^6}}}{{{x^4} - {y^4} - {x^3}y + x{y^3}}}\).

Cho 3 điểm A, B, C bất kì và một điểm O khác điểm A, B, C. Có bao nhiêu tia gốc O và đi qua một trong 3 điểm A, B, C.

Cho hình chữ nhật ABCD có AB = 4, AD = 3. Tính độ dài vectơ\(\overrightarrow {AB} + \overrightarrow {AD} \)

12 người làm xong một công việc trong 10 ngày hỏi muốn làm xong công việc trong 8 ngày thì cần bao nhiêu người? (mức làm của mỗi người như nhau)

Cho tam giác ABC vuông ở A, đường cao AH, biết BH = 9 cm, CH = 16 cm. Tính độ dài các cạnh AB, AC và chiều dài AH.

Cho \(\left( {x + \sqrt {{x^2} + 2005} } \right)\left( {y + \sqrt {{y^2} + \sqrt {2005} } } \right) = \sqrt {2005} \). Tính x + y.

Chứng minh: \(cot{\rm{ }}a--cot{\rm{ }}b{\rm{ }} = \frac{1}{{\tan a}} - \frac{1}{{\tan b}}\).

Tìm tất cả các giá trị của tham số m để đồ thị hàm số \(y = \frac{{x + 1}}{{\sqrt {{m^2}{x^2} + m - 1} }}\) có bốn đường tiệm cận.