7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 21)

Tìm x:

x ´ 8,01 – x : 100 = 38

Cho tam giác ABC vuông tại A. Đường cao AH. Kẻ phân giác của $\widehat{ACH}$ cắt AH tại M, kẻ phân giác của $\widehat{BAH}$ cắt BH tại N. Chứng minh rằng MN // AB.

Tìm x:

x × 9,8 – x : 0,25 = 18,096

Tìm x:

0,16 : (x : 3,5) = 2,8

Giải phương trình: x⁴ + 2x² – 3 = 0

Giải phương trình: x⁴ – 4x³ – 2x² + 12x + 5 = 0.

Phân tích đa thức thành nhân tử:x³ – x²y – xy² + y³.

Phân tích đa thức thành nhân tử:–6x² – 9xy + 15y².

Cho a là góc tù và $\sin \alpha =\frac{4}{5}$. Tính giá trị của biểu thức: A = 2sin a – cos a.

Cùng một lúc hai xe xuất phát từ hai địa điểm A và B cách nhau 80 km. Chúng chuyển động thẳng đều và cùng chiều từ A đến B. Xe thứ nhất khởi hành từ A với vận tốc 30 km/h. Xe thứ hai đi từ B với vận tốc 40 km/h. Tính khoảng cách giữa hai xe sau 1 giờ kể từ lúc xuất phát.

Cùng một lúc hai xe xuất phát từ hai địa điểm A và B cách nhau 160 km. Chúng chuyển động thẳng đều và cùng chiều từ A đến B. Xe thứ nhất khởi hành từ A với vận tốc 30 km/h. Xe thứ hai đi từ B với vận tốc 40 km/h. Sau khi xuất phát 1 giờ, xe thứ nhất tăng tốc và đạt tối đa vận tốc 50 km/h. Xác định thời điểm hai xe gặp nhau.

Tìm m, n nguyên dương thỏa mãn: $\frac{1}{m}+\frac{1}{n}=\frac{1}{7}$.

Tìm m, n nguyên thỏa mãn: $\frac{3}{m}+\frac{3}{n}=1$.

Đĩa xích của xe đạp có 80 răng, đĩa líp có 40 răng. Tính số truyền i và cho biết chi tiết nào quay nhanh hơn?

Giải phương trình: (x + 2)(3 – 4x) = x² + 4x + 4

Tích: 1 × 2 × 3 × 4 × 5 × … × 45 × 46 có tận cùng bao nhiêu chữ số 0?

Tích 2 × 11 × 6 × 14 × 15 × 17 × 18 × 25 × 45 có tận cùng bao nhiêu chữ số 0?

Xác định hàm số y = ax² + bx + c có giá trị nhỏ nhất bằng $\frac{3}{4}$ khi $x=\frac{1}{2}$ và nhận giá trị bằng 1 khi x = 1.

Xác định hàm số y = ax² + bx + c có giá trị nhỏ nhất bằng 2 khi x = 1 và nhận giá trị bằng 3 khi x = 2.

Cho đa thức p(x) = ax² + bx + c (với a, b, c là các số hữu tỉ). Biết P(0), P(1), P(2) là các số nguyên. Chứng minh P(x) có giá trị nguyên với mọi x nguyên.

Cho tam giác ABC có A’, B’, C’ lần lượt là trung điềm của các cạnh BC, CA, AB. Chứng minh $D\equiv B$.

Cho tam giác ABC, M điểm bất kì, G là trọng tâm. Chứng minh MA² + MB² + MC² = 3MG² + GA² + GB² + GC².

Cho nửa đường tròn đường kính AB cố định. C là một điểm trên nửa đường tròn, trên dây AC kéo dài lấy điểm D sao cho CD = CB. Tìm quỹ tích các điểm D khi C chạy trên nửa đường tròn đã cho.

Cho nửa đường tròn đường kính AB cố định. C là một điểm trên nửa đường tròn, trên dây AC kéo dài lấy điểm D sao cho CD = CB. Trên tia CA lấy điểm E sao cho CE = CB. Tìm quỹ tích các điểm E khi C chạy trên nửa đường tròn đã cho.

Có 6 quả cầu xanh đánh số từ 1 đến 6, 5 quả cầu đỏ đánh số từ 1 đến 5 và 7 quả màu vàng đánh số từ 1 đến 7. Hỏi có bao nhiêu cách lấy ra 3 quả cầu vừa khác màu vừa khác số?

Một hộp đựng 15 viên bi khác nhau gồm 4 bi đỏ, 5 bi trắng và 6 bi vàng. Tính số cách chọn 4 viên bi từ hộp đó sao cho không có đủ 3 màu.

Cho tam giác ABC, $\widehat{A}=90°$. Kẻ đường cao AH. Trên tia đối của tia HA lấy điểm K sao cho HK = HA. Chứng minh ΔABH = ΔKBH.

Cho các hàm số: y = 2x − 2 và y = (m + 1)x −𝑚² – 𝑚 (m ≠ −1). Tìm m để đồ thị hai hàm số trên là các đường thẳng song song.

Tìm m để hai đường thẳng (d): y = 3x + 1và (d′): y = (m−1)x − 2m song song với nhau.

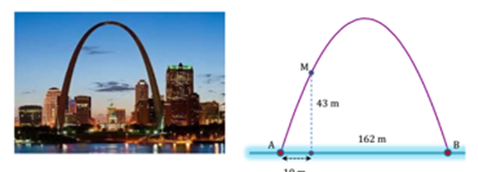
Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có độ cao 43 m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10 m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch (tính từ mặt đất đến điểm cao nhất của cổng).

Với $P={\log }_a{b}^3+{\log }_{a^2}{b}^6$ trong đó a, b là các số thực dương tùy ý và a ¹ 1. Chứng minh $P=6{\log }_{a}b$.

Cho phương trình: x² – 2(m – 1)x + m² – 3m + 4 = 0. Tìm hệ thức giữa x₁ và x₂ độc lập với m.

Cho phương trình: x² – 2(m – 1)x + m² – 3m = 0. Tìm hệ thức giữa x₁ và x₂ độc lập với m.

Tính nhanh: $A=\frac{1}{10.11}+\frac{1}{11.12}+\mathrm{...}+\frac{1}{99.100}$.

Cho nửa đường tròn tâm O đường kính AB, tiếp tuyến Ax. Gọi C là một điểm trên nửa đường tròn. Tia phân giác của $\widehat{CAx}$ cắt nửa đường tròn tại E, AE và BC cắt nhau tại K. Chứng minh: ΔABK cân tại B.

Cho ΔABC có trọng tâm G. Gọi H là điểm đối xứng của B qua G. Chứng minh $\overrightarrow{AH}=\frac{2}{3}\overrightarrow{AC}-\frac{1}{3}\overrightarrow{AB}$.

Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AB. Gọi M, N lần lượt là trung điểm của SA, SB. Chứng minh MN // (SCD).

Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AB. Gọi M, N lần lượt là trung điểm của SA, SB. Tìm P là giao điểm của SC và (ADN).

Hình thoi ABCD có diện tích 20 cm² và đường chéo AC bằng 10 cm. Tính độ dài đường chéo BD.

Hình thoi ABCD có độ dài đường chéo AC là 20 cm. Độ dài đường chéo $BD=\frac{3}{5}AC$ ​.Tính diện tích hình thoi ABCD.

Cho đường tròn (O;R), đường kính AB. Vẽ dây cung BC = R. Tính các cạch và các góc chưa biết của tam giác ABC theo R.

Cho đường tròn (O; R), đường kính AB. Vẽ dây cung BC = R. Đường thẳng qua O vuông góc với AC cắt tiếp tuyến tại A của đường tròn (O) tại D. Chứng minh DC là tiếp tuyến của đường tròn (O).

Tìm giá trị nhỏ nhất của biểu thức: A = |x – 3| + |x – 5| + |x – 7|.

Tìm giá trị nhỏ nhất của biểu thức: M = |x + 5| + |x + 2| + |x – 7| + |x – 8|

Tìm n ∈ ℤ, biết:

(n – 3) + (n – 2) + (n – 1) + … + 10 + 11 = 11.

Tìm n ∈ ℤ, biết:

(n + 1) + (n + 2) + (n + 3) + (n + 4) = 90

Đặt tính rồi tính:

15,5 : 25

Giải phương trình:|2x – 1| = 2x – 1.

Giải phương trình: (x + 3) – |x + 7| = 0.

Tìm x, y ∈ ℕ sao cho: xy + x + y = 17.

Tìm tất cả các số nguyên dương n để n² + 31 là số chính phương.

Chứng minh rằng với mọi số nguyên x, y thì:

A = (x + y)(x + 2y)(x + 3y)(x + 4y) + y⁴ là số chính phương.

Chứng minh A = n(n + 1)(n + 2)(n + 3) + 1 là số chính phương với n là số tự nhiên.

Tìm số dư của phép chia 37,99 cho 16 nếu lấy đến 2 chữ số ở phần thập phân của thương.

Tìm số dư của phép chia 32,451 chia cho 24 nếu lấy đến 3 chữ số ở phần thập phân của thương.

Tìm số tự nhiên n sao cho n² + 2n + 12 là số chính phương.

Tìm số tự nhiên n sao cho n² + 3n là số chính phương.

Giải phương trình: 46 – (x – 11) = –48.

Giải phương trình: 4x – 20 = 4

Giải phương trình:

7x³ + 12x² – 4x = 0

Giải phương trình:

x(x − 3) + 5x = x² − 8

Tìm m để hàm số $y=\sqrt{-2x+3m+2}+\frac{x+1}{2x+4m-8}$ xác định trên khoảng (−∞; −2).

Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung diểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Tứ giác ADFE là hình gì? Vì sao?

Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung diểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Tứ giác EMFN là hình gì? Vì sao?

Cho hình vẽ sau, biết đường thẳng m // n và x ^ m. Chứng minh: x ^ n.

Cho nửa đường tròn tâm O đường kính AB. Ax là tia tiếp tuyến của nửa đường tròn (Ax và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB), từ điểm C trên nửa đường tròn (C khác A, B) vẽ tiếp tuyến CM cắt Ax tại M, hạ CH vuông góc với AB, MB cắt (O) tại Q và cắt CH tại N. Chứng minh MA² = MQ . MB

Cho tam giác ABC cân tại A, I là giao điểm các đường phân giác trong tam giác. Chứng minh AC là tiếp tuyến của đường tròn tâm O ngoại tiếp tam giác BIC.

Cho tam giác ABC cân tại A, I là giao điểm các đường phân giác trong tam giác. Gọi H là trung điểm của BC, IK là đường kính của đường tròn tâm O. Chứng minh: AI. HK = AK. HI.

Cho tam giác ABC vuông tại A (AB < AC). Gọi M, N, E lần lượt là trung điểm của AB, AC, BC. Chứng minh rằng tứ giác ANEB là hình thang vuông.

Cho tam giác ABC vuông tại A (AB < AC). Gọi M, N, E lần lượt là trung điểm của AB, AC, BC. Chứng minh rằng tứ giác ANEM là hình chữ nhật.