5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 9)
49 câu hỏi
Công thức tính số tổ hợp là:
\(C_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}\);
\(C_n^k = \frac{{n!}}{{\left( {n - k} \right)!k!}}\);
\(A_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}\);
\(A_n^k = \frac{{n!}}{{\left( {n - k} \right)!k!}}\).
Phân tích đa thức thành nhân tử: x8 + x7 + 1.
Gọi a, b, c lần lượt là ba cạnh của tam giác; ha, hb, hc lần lượt là các đường cao tương ứng với ba cạnh đó và r là bán kính đường tròn nội tiếp tam giác đó. Chứng minh rằng: \(\frac{1}{{{h_a}}} + \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}} = \frac{1}{r}\).
Phân tích đa thức x5 + x + 1 thành nhân tử.
Ông và bà An cùng có 6 đứa con đang lên máy bay theo một hàng dọc. Có bao nhiêu cách xếp hàng khác nhau nếu ông hay bà An đứng ở đầu hoặc cuối hàng.
720;
1440;
18 720;
40 320.
Tìm số nguyên tố x, y thỏa mãn x2 – 2y2 = 1.
Tổng tất cả các ước của 4 là:
–7;
4;
0;
7.
Tìm x, biết: 4x2 – 25 – (2x – 5)(2x + 7) = 0.
Tìm x biết 8x3 – 12x2 + 6x – 1 = 0.
Tìm giá trị y thỏa mãn 49(y – 4)2 – 9(y + 2)2 = 0.
\(\left[ \begin{array}{l}y = \frac{{11}}{5}\\y = \frac{{17}}{2}\end{array} \right.\);
\(\left[ \begin{array}{l}y = \frac{{ - 11}}{5}\\y = 6\end{array} \right.\);
\(\left[ \begin{array}{l}y = \frac{{11}}{5}\\y = - 6\end{array} \right.\);
\(\left[ \begin{array}{l}y = \frac{{ - 11}}{5}\\y = - \frac{{17}}{2}\end{array} \right.\).
Rút gọn: A = x(5x – 3) – x2(x – 1) + x(x2 – 6x) – 10 + 3x.
Cho hai tập hợp khác rỗng: A = (m – 1; 4], B = (−2; 2m + 2), với m ∈ ℝ. Xác định m để:
a) A ∩ B = Ø;
b) A ⊂ B;
c) B ⊂ A;
d) (A ∩ B) ⊂ (−1; 3).
Phân tích đa thức thành nhân tử:A = ab(a + b) – bc(b + c) + ac (a – c).
Cho x, y, z > 0 thỏa mãn x + y + z = 1. Tìm giá trị lớn nhất của
\(Q = \frac{x}{{x + \sqrt {x + yz} }} + \frac{y}{{y + \sqrt {y + zx} }} + \frac{z}{{z + \sqrt {z + xy} }}\).
Cho tam giác ABC có P là trung điểm của AB và hai điểm M, N thỏa các hệ thức: \(\overrightarrow {MB} - 2\overrightarrow {MC} = \overrightarrow 0 \) và \(\overrightarrow {NA} + 2\overrightarrow {NC} = \overrightarrow 0 \). Chứng minh rằng 3 điểm M, N, P thẳng hàng.
Phân tích đa thức thành nhân tử: (ab – 1)2 + (a + b)2.
Tính A = 1.2 + 2.3 + 3.4 +…+ n(n + 1).
Khổ giấy A1 lớn gấp bao nhiêu lần khổ giấy A3?
4 lần;
8 lần;
6 lần;
16 lần.
Cho hai hàm số y = x2 và y = mx + 4, với m là tham số. Khi m = 3, tìm tọa độ các giao điểm A, B của hai đồ thị của hai hàm số trên.
Cho hai tập hợp khác rỗng A = (m – 1; 4]; B = (−2; 2m + 2), m ∈ ℝ. Tìm m để A ∩ B ≠ Ø.
−2 < m < 5;
m > −3;
−1< m < 5;
1 < m < 5.
Tìm tất cả số tự nhiên x, y sao cho 2x + 5y là số chính phương.
Một bó hoa 12 bông gồm: 5 hoa hồng, 4 hoa lan còn lại là hoa cúc. Chọn ngẫu nhiên 5 bông hoa. Tính xác suất sao cho chọn đủ ba loại và số cúc không ít hơn 2.
\(\frac{{115}}{{396}}\);
\(\frac{{18}}{{35}}\);
\(\frac{1}{{30}}\);
\(\frac{2}{{30}}\).
Trong khai triển (x – 2)100 = a0 + a1x1 + … + a100x100. Tổng hệ số
a0 + a1 + a2 + … + a100 bằng:
−1;
1;
3100;
2100.
Tính tổng min và max của hàm số: \[y = \sqrt {2 + x} + \sqrt {2 - x} + 2\sqrt {4 - {x^2}} \].
Hình lăng trụ có thể có số cạnh nào sau đây?
2015;
2017;
2018;
2016.
Phân tích đa thức thành nhân tử x2 + 5x – 6.
Công thức tính diện tích tam giác đều cạnh a.
Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau:
x | −∞ 1 2 3 4 +∞ |
f’(x) |
− 0 + 0 − 0 − 0 + |
Hàm số y = 3f(x + 2) – x3 + 3x đồng biến trên khoảng nào dưới đây?
(1; +∞);
(−∞; 1);
(−1; 0);
(0; 2).
Cho đồ thị hàm số y = f(x) có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình \(f(x) = \frac{1}{2}\) là:
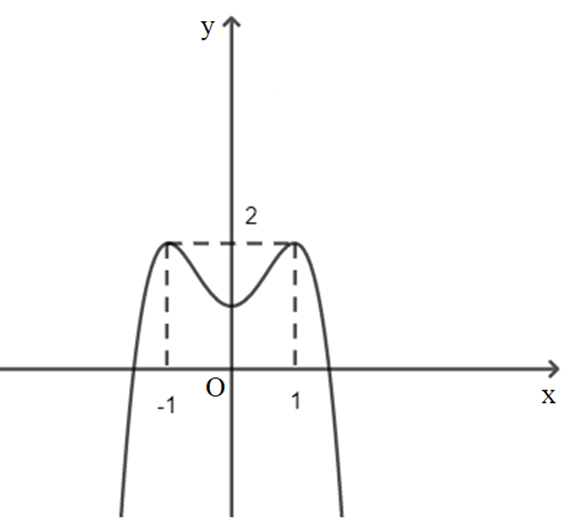
2;
4;
1;
3.
Tìm số nguyên tố p để p + 2 và p + 10 cũng là số nguyên tố.
Phân tích đa thức sau thành nhân tử: x2 – 2x – 4y2 – 4y.
Một lớp học có 25 học sinh học khá các môn tự nhiên, 24 học sinh học khá các môn xã hội, 10 học sinh học khá cả môn tự nhiên lẫn môn xã hội, đặc biệt vẫn còn 3 học sinh chưa học khá cả hai nhóm môn ấy. Hỏi lớp có bao nhiêu học sinh chỉ khá đúng một nhóm môn (tự nhiên hoặc xã hội).
39;
26;
29;
36.
Phát biểu nào sau đây đúng?
Tổng của hai vectơ khác \(\overrightarrow 0 \) là một vectơ khác \(\overrightarrow 0 \).
Hai vectơ cùng phương với một vectơ khác \(\overrightarrow 0 \) vectơ thì hai vectơ đó cùng phương với nhau.
Hiệu của hai vectơ có độ dài bằng nhau là \(\overrightarrow 0 \).
Hai vectơ không bằng nhau thì có độ dài không bằng nhau.
Tổng các góc của hình thang cân là bao nhiêu?
180°;
360°;
90°;
720°.
Chứng minh tích của 4 số tự nhiên liên tiếp chia hết cho 24.
Định lý talet trong tam giác.
Cho hàm số bậc nhất y = (2m – 1)x + m – 1 (d). Tìm m để khoảng cách từ O(0; 0) đến (d) là \(\sqrt 3 \).
Tìm x biết:
\(\frac{1}{3}x + \frac{2}{5}\left( {x + 1} \right) = 0\).
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình 16x – m4x+1 + 5m2 – 45 = 0 có hai nghiệm phân biệt. Hỏi S có bao nhiêu phần tử?
13;
3;
6;
4.
Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \frac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) trên [−4; 0] lần lượt M và m. Giá trị của M + m bằng:
\(\frac{4}{3}\);
\(\frac{{ - 28}}{3}\);
−4;
\(\frac{{ - 4}}{3}\).
Rút gọn biểu thức: 3x(x – 2) – 5x(1 – x) – 5(x2 – 3).
Phân tích đa thức x2 – 2x – 15.
Cho hai số a, b thỏa mãn điều kiện a + b = 1.
Chứng minh a3 + b3 + ab \( \ge \frac{1}{2}\).
Người ta muốn xây một cái bể chứa nước dạng khối hộp chữ nhật không nắp có thể tích \(\frac{{500}}{3}\) m3. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là 500 000 đồng/m3. Nếu biết xác định kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất, chi phí thấp nhất đó là:
70 triệu đồng;
85 triệu đồng;
80 triệu đồng;
75 triệu đồng.
Một liên đoàn bóng rổ có 10 đội, mỗi đội đấu với mỗi đội khác 2 lần, một lần ở sân nhà và một lần ở sân khách. Số trận đấu được sắp xếp là bao nhiêu?
45;
90;
100;
180.
Tìm giá trị lớn nhất của biểu thức \(A = 11 - \sqrt {{x^2} + 7x + 4} \).
Cho các vecto \(\overrightarrow a ;\overrightarrow b \ne 0\). Khẳng định nào sau đây đúng?
\(\overrightarrow a ;\overrightarrow b \) cùng phương khi và chỉ khi \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\);
\(\overrightarrow a \); \(\overrightarrow b \) cùng phương khi và chỉ khi \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\);
\(\overrightarrow a \); \(\overrightarrow b \) cùng phương khi và chỉ khi \(\overrightarrow a .\overrightarrow b \ne \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\);
\(\overrightarrow a \); \(\overrightarrow b \) cùng phương khi và chỉ khi \(\left| {\overrightarrow a .\overrightarrow b } \right| = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\).
Chứng minh n3 – n chia hết cho 3 với mọi số nguyên n.
Tìm x biết: (x – 5)(x – 4) – (x + 1)(x – 2) = 7.








