5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 85)
118 câu hỏi
Cho a + b + c = 2. Tìm giá trị lớn nhất của:
Cho hàm số y = ax4 + bx2 + c có đồ thị như hình vẽ bên.
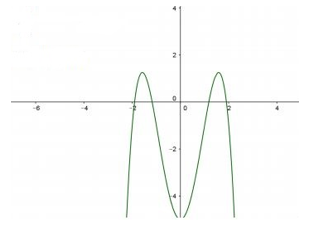
Mệnh đề nào dưới đây đúng?
a > 0, b < 0, c > 0;
a < 0, b > 0, c < 0;
a < 0, b < 0, c < 0;
a > 0, b < 0, c < 0.
Cho hình hộp ABCD.A’B’C’D’ có chiều cao bằng 6, diện tích đáy bằng 8. Gọi M là trung điểm AB. Mặt phẳng (A’C’M) cắt BC tại N. Tính thể tích của khối đa diện có các đỉnh là D, M, N, A’, C’.
10;
18;
12;
24.
Cho hình hộp ABCD.A’B’C’D’. Gọi M là điểm trên cạnh AC sao cho AC = 3MC. Lấy N trên cạnh C’D sao cho C’N = xC’D. Với giá trị nào của x thì MN // BD’.
Một hình hộp chữ nhật ABCD.A’B’C’D’có ba kích thướclà 2cm,3cm và 6cm. Thể tích của khối tứ diện ACB’D’ bằng:
12 cm3;
8 cm3;
6 cm3;
4 cm3.
Cho tam giác ABC đều cạnh a. Gọi M là trung điểm BC. Khẳng định nào sau đây đúng?
= a
Chứng minh a2 + b2 + c2 + 3 ≥ 2(a + b + c).
Chứng minh rằng:
a) (a + b + c)2 ≤ 3(a2 + b2 + c2)
b) (a + b)2 ≤ 2(a2 + b2)
Tính tổng
S = 2n – 1;
S = 2n;
S = 2n-1;
S = 2n + 1.
Cho phương trình x2 – mx + m – 1 = 0 (m là tham số)
a) Giải phương trình với m = 3.
b) Tìm tất cả các giá trị m để phương trình có 2 nghiêm x1, x2 thỏa mãn x1 – 2x2 = 3.
Giải phương trình:
Giải phương trình x2 – 2nx – 5 = 0. Biết số nguyên dương n thỏa mãn: .
;
x = ±4;
Phương trình 32x+1 – 4.3x + 1 = 0 có nghiệm x1, x2 với x1 < x2. Chọn phát biểu đúng?
x1.x2 = –1;
2x1 + x2 = 0;
x1 + 2x2 = –1;
x1 + x2 = 2.
Giải phương trình: log2x.log2(2x) – 2 = 0
Một học sinh muốn chọn 20 trong 30 câu trắc nghiệm. Học sinh đó đã chọn được 5 câu. Tìm số cách chọn các câu còn lại?
Tổng các nghiệm của phương trình bằng:
3;
1;
2;
0.
Phương trình
Vô nghiệm;
Có một nghiệm âm;
Có một nghiệm âm và một nghiệm dương;
Có hai nghiệm dương.
Phương trình có số nghiệm là
1;
2;
3;
4.
Số nghiệm thực của phương trình là:
1;
2;
3;
0.
Trong hệ trục tọa độ Oxy cho hình bình hành OABC, điểm C thuộc trục hoành. Khẳng định nào sau đây đúng?
có tung độ khác 0;
Hai điểm A, B có tung độ khác nhau;
C có hoành độ bằng 0;
xA + xC – xB = 0
Trong mặt phẳng với hệ tọa độ Oxy cho hình bình hành OABC có tọa độ điểm A(3;1), C(–1;2) (tham khảo hình vẽ bên).
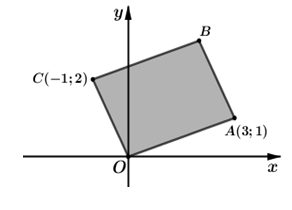
Số phức nào sau đây có điểm biểu diễn là điểm B?
z1 = –2 + 3i;
z2 = 2 + 3i;
z3 = 4 – i;
z4 = –4 + i.
Trong hệ tọa độ Oxy, cho ba điểm A(1; 3); B(–1; 2); C(–2; 1). Tìm tọa độ của vectơ
(–5; –3);
(1; 1);
(–1; 2);
(–1; 1).
Trong hệ tọa độ Oxy, cho ba điểm A(1; 1); B(2; –1); C(4; 3). Tọa độ điểm D để ABDC là hình bình hành là
D(1; 3);
D(3; 5);
D(3; 1);
D(5; 1).
Tìm số hạng chứa x trong khai triển .
144x;
–72x;
–84x;
132x.
Tìm x biết: x3 + 27 + (x + 3)(x – 9) = 0.
Gọi X là tập hợp các số tự nhiên gồm 6 chữ số đôi một khác nhau được tạo thành từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9. Chọn ngẫu nhiên một số từ tập hợp X. Tính xác suất để số được chọn chỉ chứa 3 chữ số lẻ.
a) Tìm các ước của mỗi số sau: 2, 3, 4, 5, 6, 7, 17, 34.
b) Trong các số trên, những số nào có hai ước, những số nào có nhiều hơn hai ước?
Số lượng các nghiệm của bất phương trình .
9;
11;
12;
10.
Phân tích đa thức thành nhân tử: (x – y)2 + 4(x – y) – 12.
Giải phương trình: (x + 1)(x² – x + 1) – 2x = x(x – 1)(x + 1).
Giải phương trình:
Cho a, b > 0 thỏa mãn . Chứng minh a + b ≥ 2.
Chứng minh rằng:
Cho 3 số dương a, b, c thỏa mãn: a + b + c + ab + ca + bc = 6abc.
Chứng minh rằng: .
Thực hiện phép tính: (4x – 1)(2x2 – x – 1).
Rút gọn biểu thức: với x > 0, x ≠ 4
Tập nghiệm S của bất phương trình là:
S = [3; +∞);
S = (3; +∞);
S = {2} ∪ [3; +∞);
S = {2} ∪ (3; +∞).
Cho giá trị gần đúng là 0,429. Sai số tuyệt đối của số 0,429 là:
0,0001;
0,0003;
0,0005;
0,0006.
Chứng minh:
Độ dài đường sinh của một hình nón bằng 2a. Thiết diện qua trục của nó là một tam giác cân có góc ở đỉnh bằng 120° Diện tích toàn phần của hình nón là:
Đồ thị hàm số nào dưới đây nhận trục tung làm trục đối xứng?
y = sin x – cos x;
y = 2sin x;
y = 2sin (–x);
y = –2cos x.
Một hộp đựng 9 viên bi trong đó có 4 viên bi màu đỏ, 5 viên bi màu xanh. Lấy ngẫu nhiên 3 viên bi. Tính xác suất để trong 3 viên bi lấy được có ít nhất 2 viên bi màu xanh.
Một hộp đựng 5 bi đỏ, 2 bi đen và 4 bi trắng. Lấy ngẫu nhiên 2 bi từ trong hộp
a) Tính xác suất để được 2 bi khác màu
b) Tính xác suất để được ít nhất 1 bi đỏ.
Nếu lấy 3,14 làm giá trị gần đúng của π thì sai số tuyệt đối là:
0,001;
0,002;
0,003;
0,01.
Tính diện tích của mặt cầu ngoại tiếp hình tứ diện đều cạnh a.
2πa23;
3πa22;
3πa24;
4πa23.
Phương trình có tập nghiệm là
{2;8}
Thiết diện qua trục của một hình trụ là một hình vuông có cạnh bằng 2a. Tính theo a thể tích khối trụ đó.
πa3;
2πa2;
4πa3;
23πa3.
Trong không gian cho ba điểm phân biệt không thẳng hàng, ta có thể xác định được nhiều nhất bao nhiêu mặt phẳng phân biệt?
1;
2;
3;
4
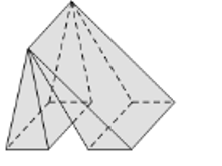
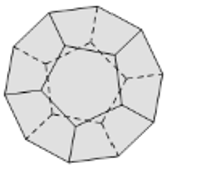
Vật thể nào dưới đây không phải là khối đa diện?
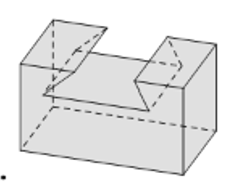
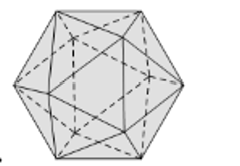
Phân tích các đa thức sau thành nhân tử
a) x2 + 4xy – 21y2
b) 5x2 + 6xy + y2
c) x2 + 2xy – 15y2
d) (x – y)2 + 4(x – y) – 12
e) x2 – 7xy + 10y2
f) x2yz + 5xyz – 14yz
g) x4 + 4x2 – 5
h) x3 – 19x – 30
i) x3 – 5x2 – 14x
j) x3 – 7x – 6
k) x3 – 5x2 – 14
Liệt kê các số nguyên tố có 2 chữ số nhỏ hơn 25
Tìm số tiệm cận đứng và ngang của đồ thị hàm số
2;
3;
1;
0.
Tất cả điều kiện của tham số thực m sao cho đồ thị hàm số có đúng 1 tiệm cận đứng là:
–5 ≤ m < –1
Tính tổng:
316;
416;
216;
516.
Chứng minh rằng:
a) a2 + b2 ≥ 0.
b) m2 + n2 + 2 ≥ 2(m + n).
c) với a, b > 0.
Khi phương trình bậc hai ax2 + bx + x = 0 có biệt thức D = b2 – 4ac < 0 thì có bao nhiêu nghiệm?
Trong mặt phẳng tọa độ Oxy cho đường thẳng d: x – 2y + 3 = 0 và I(1; –2). Viết phương trình đường thẳng d' sao cho d’ là ảnh của đường thẳng d qua phép đối xứng tâm I.
Cho a, b, c là những số nguyên thỏa mãn:
Chứng minh: a3 + b3 + c3 chia hết cho 3.
Cho hàm số f(x) liên tục trên ℝ thỏa mãn f(3x) = f(x) – 2x, ∀x ∈ ℝ và . Tính I = .
I = 7;
I = 12;
I = 4;
I = 10;
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình.
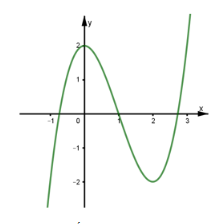
Gọi m là số nghiệm của phương trình f(f(x)) = 1. Khẳng định nào sau đây là đúng?
m = 6;
m = 7;
m = 5;
m = 9.
Cho hình lăng trụ ABC.A'B'C' có thể tích là V. Gọi M là điểm thuộc cạnh CC' sao cho CM = 3C'M. Tính thể tích khối chóp M.ABC
V4;
3V4;
V12;
V6.
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, AC = 2a, SA vuông góc với mặt phẳng (ABCD), SC tạo với mặt phẳng (SAB) một góc 30o. Gọi M là một điểm trên cạnh AB sao cho BM = 3MA. Khoảng cách từ điểm A đến mặt phẳng (SCM) là:
Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn. Kẻ 2 tiếp tuyến AM, AN và cát tuyến ABC với đường tròn (AB < AC). Qua O kẻ OK vuông góc với BC tại K, OK cắt MN tại S. Chứng minh SC là tiếp tuyến của đường tròn (O).
Tập nghiệm của phương trình 2sin2x + 1 = 0 là:
Tìm phần thực, phần ảo của số phức
Phần thực: a = 2, phần ảo: b = -4i;
Phần thực: a = 2, phần ảo: b = -4;
Phần thực: a = 2, phần ảo: b = 4i;
Phần thực: a = 2, phần ảo: b = 4.
Tính chu vi hình thang biết đáy lớn bằng 14cm, đáy bé bằng 10cm, 2 cạnh bên lần lượt bằng 6cm, và 8cm.
36 cm;
38 cm;
32 cm;
34 cm.
Xét số phức z thỏa mãn là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn các số phức z luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng:
1
2
Giải phương trình sau (12x + 7)2 (3x + 2) (2x + 1) = 3
Tìm GTNN của với x > 0.
Thực hiện phép tính:
a) 483 + (-56) + 263 + (-64)
b) 371 + (-531) + (-271) + 731
c) 3251 – 243 - 3250
d) 279 – (145 + 279)
Tính hợp lí:
a) 942 – 2567 + 2563 – 1942
b) 42.53 + 47.156 – 47.114
Cho a, b, c > 0. Chứng minh rằng:
Cho tam giác MNP vuông tại M, đường cao MH. Biết NH = 5 cm, HP = 9 cm. Độ dài MH bằng:
4 cm;
7 cm;
cm;
4,5 cm.
Cho tứ diện ABCD. Gọi M là trung điểm cạnh AB, N thuộc cạnh AC sao cho AN=2NC, P thuộc cạnh BD sao cho BP = 3PD.
a) Xác định giao tuyến của hai mặt phẳng (MNP) và (BCD).
b) Xác định giao điểm I của đường thẳng CD và mặt phẳng (MNP); giao điểm J của đường thẳng AD và mặt phẳng (MNP). Từ đó suy ra ba điểm N, I, J thẳng hàng.
c) Giả sử điểm P di động trên cạnh BD. Gọi K là giao điểm của MI và NP. Chứng minh K thuộc một đường thẳng cố định.
Cho tứ diện ABCD có I, J lần lượt là trung điểm AC, BC. Gọi K thuộc BD sao cho KD < KB. Gọi E là giao điểm của JK và CD, F là giao điểm của AD và IE. Giao tuyến của (IJK) và (ACD) là:
đường thẳng AI;
đường thẳng IF;
đường thẳng JE;
đường thẳng IE.
Cho đoạn thẳng AB và M là một điểm nằm trên đoạn AB sao cho AM = AB. Giá trị của k để có đẳng thức là:
k = ;
;
5;
-5.
Chứng minh rằng: x2 + y2 +z2 ≥ xy + yz + xz với mọi x, y, z.
Cho x2 + y2 +z2 = xy + yz + xz. Chứng minh z = x = y.
Hình nón có thiết diện qua trục là tam giác đều và có thể tích . Diện tích xung quanh S của hình nón đó là:
Tìm m nguyên để hệ phương trình sau có nghiệm duy nhất là nghiệm nguyên.
a)
b)
Tìm tập xác định của hàm số y = (7x)2 + x – 2.
Trong không gian với hệ tọa độ Oxyz, tìm bán kính R của đường tròn giao tuyến của mặt phẳng 2x – 2y – z + 9 = 0 và mặt cầu x2 + y2 + z2 – 6x + 4y – 2z – 86 = 0.
R = 9;
R = 4;
R = 2;
R = 8.
Tính bán kính đường tròn giao tuyến của mặt cầu S(O;r) và mặt phẳng (α) biết rằng khoảng cách từ tâm O đến (α) bằng
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = 2a, AD = DC = a, SA = a , SA ⊥ (ABCD). Tính cosin của góc giữa hai mặt phẳng (SBC) và (SCD).
Tính
Tìm tập xác định của hàm số
Tìm tập xác định của hàm số
Tập xác định của hàm số là:
ℝ \ {1};
ℝ \ {2};
ℝ \ {-1};
ℝ \ {-2}.
Tìm giá trị nhỏ nhất m của hàm số: trên đoạn
m = 3;
m = 5;
m = ;
m = 4.
Phân tích đa thức sau thành nhân tử x2 –xy + x – y
Đội thanh niên xung kích có của một trường phổ thông có 12 học sinh, gồm 5 học sinh lớp A, 4 học sinh lớp B và 3 học sinh lớp C. Cần chọn 4 học sinh đi làm nhiệm vụ sao cho 4 học sinh này thuộc không quá 2 trong ba lớp trên. Hỏi có bao nhiêu cách chọn như vậy?
225;
495;
372;
219.
Giải phương trình (x2 − 1)(x2 + 4x + 3) = 192
Thực hiện phép tính:
a) 17 – 25 + 55 – 17
b) 25 – (-75) + 32 – (32 + 75)
c) (-5).8.(-2).3
d) (-15) + (-122)
e) (7 – 10) + 3
f) |-127| – 18.(5 – 6)
Tìm giá trị nhỏ nhất của C(x) = 3x2 + x -1
Rút gọn các phân thức:
Chứng minh rằng , với mọi a, b không âm
Cho hàm số y = f(x) thỏa mãn f’(x) = x2 – 5x + 4. Khẳng định nào sau đây đúng?
Hàm số đã cho đồng biến trên khoảng (-∞; 3);
Hàm số đã cho nghịch biến trên khoảng (3; +∞);
Hàm số đã cho nghịch biến trên khoảng (2; 3);
Hàm số đã cho đồng biến trên khoảng (1; 4).
Cho hàm số . Khẳng định nào sau đây đúng?
Hàm số đồng biến trên khoảng (-∞; 1) ∪ (1; +∞);
Hàm số nghịch biến trên khoảng (-∞; 1) và (1; +∞);
Hàm số nghịch biến trên khoảng (-∞; 1) và (1; +∞);
Hàm số nghịch biến trên ℝ \ {1}.
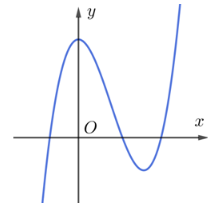
Cho hàm số y = ax3 + 3x + d (a, d ∈ ℝ) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?
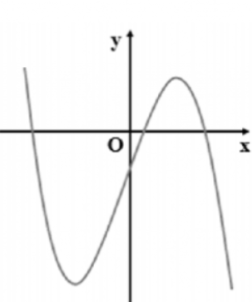
a > 0, d > 0;
a < 0, d > 0;
a > 0, d < 0;
a < 0, d < 0.
Cho hàm số y=f(x) có đồ thị trên một khoảng K như hình vẽ bên. Trên K, hàm số có bao nhiêu cực trị?
3;
2;
0;
1.
Cho ∆ABC có Â < 90o. Vẽ ra phía ngoài tam giác đó hai đoạn thẳng AD vuông góc và bằng AB; AE vuông góc và bằng AC.
a) Chứng minh: DC = BE và DC ⊥ BE
b) Gọi N là trung điểm của DE. Trên tia đối của tia NA lấy M sao cho NA = NM. Chứng minh: AB = ME và ∆ABC = ∆EMA.
c) Chứng minh: MA ⊥ BC.
Cho tam giác ABC vuông tại A với AB = a, AC = 2a quay xung quanh cạnh AB ta được một khối nón tròn xoay có đường sinh l bằng bao nhiêu ?
l = a ;
l = a ;
l = 3a;
l = 2a .
Cho tam giác ABC với A(-3; 6); B(9; -10) và G là trọng tâm. Tìm tọa độ điểm C
C(5; -4);
C(5; 4);
C(-5; 4);
C(-5; -4).








