5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 84)

Chứng minh nếu p và 8p² + 1 là hai số nguyên tố lẻ thì 8p² + 2p + 1 là số nguyên tố.

Cho hình bình hành ABCD. Lấy điểm E trên cạnh AB, điểm F trên cạnh CD sao cho AE = CF. Chứng minh rằng ba đường thẳng AC, BD, EF đồng quy.

Cho hàm số y = – x³ + (2m + 1)x² – (m² – 3m + 2)x – 4 (C_m) với m là tham số

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 1. 

b) Tìm m để đồ thị hàm số (C_m) có các điểm cực đại và cực tiểu nằm về hai phía của trục tung.

Phát biểu định lí về hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba.

Cho đường thẳng d: y = 2x + 6. Giao điểm của d với trục tung là:

Cho hàm số y = x³ – 3x² – 3x – 2 có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C) tại giao điểm của (C) với trục tung.

Một hình thang có đáy nhỏ là 4 cm , chiều cao là 5 cm, diện tích là 40 cm². Tính chiều dài đáy lớn.

Giải phương trình: log₂x + log₃x + log₄x = log₂₀x.

Tổng của tất cả các số nguyên a mà –7 < a ≤ 7 là:

Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?

Tìm giá trị nhỏ nhất của  $A=\frac{1}{xy}+\frac{1}{\text{yz}}+\frac{1}{z\text{x}}$ (x, y, z > 0) biết x² + y² + z² ≤ 3.

Tìm m để hệ bất phương trình $\left\{\begin{array}{l}x-1>0\\ x^2-2m\text{x}+1\le 0\end{array}\right.$ có nghiệm.

Giải phương trình: 3x² – x – 1 = 0.

Cho phương trình  $\cot \text{x}=\sqrt{3}$. Các nghiệm của phương trình là:

Giải phương trình  $4\sqrt{x+3}-\sqrt{x-1}=x+7$.

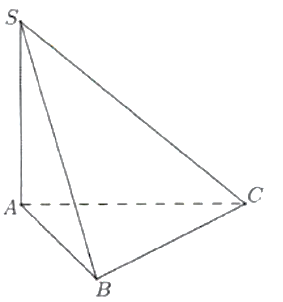
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa SA và mặt phẳng (SBC) bằng 45° (tham khảo hình bên). Thể tích của khối chóp S.ABC bằng:

Cho tam giác ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.

Một cấp số cộng gồm 5 số hạng. Hiệu số hạng đầu và số hạng cuối bằng 20. Tìm công sai d của cấp số cộng đã cho

Giải phương trình  $\mathrm{s}\text{inx}+\cos x.\sin 2\text{x}+\sqrt{3}cos3\text{x}=2\left(cos4\text{x}+{\sin }^{3}x\right)$.

Tìm số điểm cực trị của hàm số y = sinx – cos²x trên [0; 2π].

Tìm giá trị nhỏ nhất của biểu thức x² + y² + xy – 3x – 3y – 3.

Tìm giá trị nhỏ nhất của biểu thức A = x² + 5x + 7.

Cho phương trình  $\frac{x-b-c}{a}+\frac{x-c-a}{b}+\frac{x-a-b}{c}-3=0$ (với abc ≠ 0 và bc + ac + ab ≠ 0). Trong các kết luận sau, kết luận đúng là:

Phân tích đa thức thành nhân tử: x³ – 7x – 6.

Xét tính đúng sai của mỗi mệnh đề sau và phát biểu phủ định của nó.

a)  $\sqrt{3}+\sqrt{2}=\frac{1}{\sqrt{3}-\sqrt{2}}$.

b)  ${\left(\sqrt{2}-\sqrt{18}\right)}^2>8$.

c)  ${\left(\sqrt{3}+\sqrt{12}\right)}^2$ là một số hữu tỉ.

d) x = 2 là một nghiệm của phương trình  $\frac{x^2-4}{x-2}=0$.

Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; –1; 3) và hai đường thẳng  $d_1:\frac{x-4}{1}=\frac{y+2}{4}=\frac{z-1}{-2};d_2:\frac{x-2}{1}=\frac{y+1}{-1}=\frac{z-1}{1}$. Viết phương trình đường thẳng d đi qua điểm A, vuông góc với đường thẳng d₁ và cắt đường thẳng d₂.

Trong không gian Oxyz, cho 2 điểm A(1; 2; –3), M(–2; –2; 1) và đường thẳng  $d:\frac{x+1}{2}=\frac{y-5}{2}=\frac{z}{-1}$. ∆ là đường thẳng đi qua M và vuông góc với đường thẳng d đồng thời cách A một khoảng lớn nhất, khi đó ∆ đi qua điểm nào trong các điểm sau:

Cho A = [m; m + 1] và B = (–1; 3). Điều kiện để (A ∩ B) = ∅ là gì?

Thực hiện phép tính:  $\left(\frac{5}{7}-\frac{7}{5}\right)-\left[\frac{1}{2}-\left(-\frac{2}{7}-\frac{1}{10}\right)\right]$.

Một hộp đựng có 4 bi đỏ, 5 bi xanh và 7 bi vàng. Hỏi có bao nhiêu cách lấy được 3 viên bi trong đó chỉ có hai màu.

Tìm x, y, z thỏa mãn: x² + y² + 2z² + xy + 2yz + 2zx + x + y + 1 = 0.

Tìm x: 4x² – 25 = 0.

Cho hàm số y = – x³ + 3mx² – 3m – 1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số đã cho có hai điểm cực trị đối xứng với nhau qua đường thẳng d: x + 8y – 74 = 0.

Chứng minh rằng 7 . 52n + 12 . 6n chia hết cho 19.

Cho a, b, n thuộc ℕ. Hãy so sánh  $\frac{a+n}{b+n}$ và  $\frac{a}{b}$.

Tính nhanh: 50² – 49² + 48² – 47² + ... + 2² – 1².

Cho tam giác ABC vuông tại A có  $\widehat{B}=60°$. Trên cạnh BC lấy điểm M sao cho  $\widehat{CAM}=30°$. Chứng minh rằng:

a) Tam giác CAM cân tại M;

b) Tam giác BAM là tam giác đều;

c) M là trung điểm của đoạn thẳng BC.

Chứng minh  $\frac{1}{2\sqrt{1}}+\frac{1}{3\sqrt{2}}+\frac{1}{4\sqrt{3}}+\mathrm{...}+\frac{1}{2005\sqrt{2004}}<2$.

Với a dương, chứng minh  $a+\frac{1}{a}\ge 2$.

Cho nửa đường tròn (O), đường kính AB và điểm C thuộc nửa đường tròn đó. Từ C kẻ CH vuông góc với AB (H thuộc AB). Gọi M là hình chiếu của H trên AC, N là hình chiếu của H trên BC.

a) Chứng minh tứ giác HMCN là hình chữ nhật.

b) Chứng minh MN là tiếp tuyến của đường tròn đường kính BH.

c) Chứng minh MN vuông góc với CO.

d) Xác định vị trí của điểm C trên nửa đường tròn đường kính AB để đoạn thẳng MN có độ dài lớn nhất.

Rút gọn biểu thức:

$P=\frac{x\sqrt{x}-1}{x-\sqrt{x}}-\frac{x\sqrt{x}+1}{x+\sqrt{x}}+\frac{x+1}{\sqrt{x}}$

Tìm m để phương trình  $m=\frac{\cos x+2\text{sinx}+3}{2c\text{osx}-\mathrm{s}\text{inx}+4}$ có nghiệm

Giải phương trình sin²x + sin²2x = 1.

Trong mặt phẳng tọa độ Oxy cho I(2; 1) và đường thẳng d: 2x + 3y + 4 = 0. Ảnh của d qua Q_{(I; 45°)} là:

Tìm tất cả các giá trị thực của tham số m để phương trình x³ – 3mx + 2 = 0 có nghiệm duy nhất

Xác định giá trị của x để số dư trong phép chia sau bằng 0:

(3x⁵ – x⁴ – 2x³ + x² + 4x + 5) : (x² – 2x+ 2).

Tập xác định của hàm số y = cotx là:

Giải phương trình:

$\frac{x-5}{100}+\frac{x-4}{101}+\frac{x-3}{102}=\frac{x-100}{5}+\frac{x-101}{4}+\frac{x-102}{3}$

Tính:  $\frac{x^6-y^6}{x^4-y^4-x^{3}y+x{y}^3}$.