5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 8)

b) Tính diện tích của ∆AOB (đơn vị đo trên các trục tọa độ là xen ti mét)

Cho hàm số bậc nhất y = (m − 1)x + 3 (1) (với m ≠ 1)a) Xác định m để đồ thị hàm số (1) song song với đường thắng y = −x + 1

b) Xác định m để đường thắng y =1 − 3x , đường thẳng y= −0,5x − 1,5 và đồ thị hàm số (1) cùng đi qua một điểm.

Cho hàm số bậc nhất y= (m − 1)x+m − 3 (m ≠ 1) có đồ thị là đường thẳng d.

a) Khi m = 0, hãy vẽ đồ thị hàm số trên;

b) Tìm m để d cắt trục tung tại điểm có tung độ bằng 1;

c) Gọi A, B lần lượt là giao điểm của d với hai trục Ox,Oy. Tìm m để tam giác OAB cân.

Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I (I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC (E khác B và C), AE cắt CD tại F. Chứng minh:

a) BEFI là tứ giác nội tiếp đường tròn.

b) AE . AF = AC².

c) Khi E chạy trên cung nhỏ BC thì tâm đường tròn ngoại tiếp ∆CEF luôn thuộc một đường thẳng cố định.

Cho đường tròn (O) bán kính R, đường kính AB, vẽ dây cung CD vuông góc với AB(CD không đi qua (O)), trên tia đối của BA lấy S, SC cắt đường tròn tại M thuộc cung nhỏ BC

a) Chứng minh ∆SMA ᔕ∆SBC.

b) Gọi H là giao điểm của MA và BC, K là giao điểm của MD và AB. Chứng minh tứ giác BMHK nội tiếp và HK // CD.

c) Chứng minh OK . OS=R².

Số đo các góc của một đa giác lồi có 9 cạnh lập thành một cấp số cộng có công sai d = 3°. Tìm số đo của các góc đó

Tổng số đo các góc của đa giác đều 9 cạnh là:

Viết phương trình đường thẳng đi qua 2 điểm A(1; 2) và B(3; 4).

Viết phương trình đường thẳng đi qua 2 điểm A(−1; −2) và B(3; −10)

Xác định hàm số bậc hai thỏa mãn điều kiện.

a) Cho (P): y = ax² + bx + c. Tìm a, b, c biết (P) đi qua điểm A(1; 2) và có đỉnh I(−1; −2).

b) Tìm hàm số y = ax² + bx − 3 biết đồ thị có tọa độ đỉnh là $I\left(\frac{1}{2};-5\right)$

Tìm m để đồ thị hàm số y = x² − mx + 1 đi qua điểm M(1; 2)

Cho hàm số y=f(x) có bảng xét dấu đạo hàm như sau

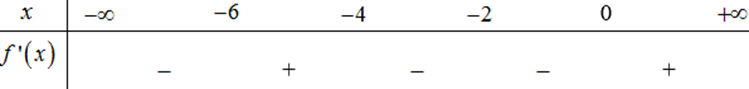
Hàm số f(2x − 2) − 2e^xnghịch biến trên khoảng nào dưới đây?

Giải phương trình: $2x^2+3x+\sqrt{2x^2+3x+9}=33$

Phương trình $2x^2+3x+\sqrt{2x^2+3x+9}=33$ có hai nghiệm là x₁, x₂. Tích x₁x₂ bằng:

Cho hàm số y = 3x − 2

a) Xác định các hệ số a, b. Tìm hai điểm thuộc đồ thị hàm số trên.

b) Tìm m để đường thẳng y =3x − 2 cắt đường thẳngy = mx + 2.

Cho hàm số y = 3x – 2. Vẽ đồ thị (d) của hàm số.

Cho tam giác ABC vuông tại A, đường cao AH, AB=6 cm, AC= 8cm.
a) Tính BC, BH, HC, AH .

b) Kẻ phân giác AD. Tính BD, DC.

c) Tính diên tích tam giác AHD.

Cho ∆ABC vuông tại A vẽ đường cao AH có AB=6 cm, AC= 8cm.

a) Chứng minh ∆HBA ᔕ ∆ABC.

b) Tính BC, AH, HC.

c) Chứng minh AH² = HB.HC.

a) Tìm hệ số của x¹²y¹³ trong khai triển (x+y)²⁵.

b) Tìm hệ số của x¹²y¹³ trong khai triển (x − y)²⁵.

Tìm hệ số của x¹²y¹³ trong khai triển (2x+3y)²⁵.

Cho hàm số bậc bốn f(x) có bảng biến thiên như sau:

Số điểm cực trị của hàm số g(x)=x²[f(x−1)]⁴là:

Cho hàm số bậc bốn f(x) có bảng biến thiên như sau:

Số điểm cực trị của hàm số g(x)=x⁴[f(x−1)]²là:

Cho hàm số: y = x³ − 3mx² + 9x + 1, có đồ thị (Cm), với m là tham số. Tìm giá trị của tham số m để đường thẳng (dm): y = x + 10 − 3m cắt đồ thị (Cm) tại 3 điểm phân biệt A, B, C. Gọi k₁, k₂, k₃ là hệ số góc tiếp tuyến của (Cm) lần lượt tại A, B, C. Tìm giá trị của m để k₁ + k₂ + k₃ > 15.

Giá trị nào của m để điểm I(−1;6) là điểm cực đại của đồ thị hàm số y = x³ − 3mx² − 9x + 1(Cm).

Tìm điều kiện của tham số m để hàm số là hàm số bậc nhất:

a) $y=\sqrt{5-m}\left(x-1\right)$

b) $y=\frac{m+1}{m-1}x+3,5$

Cho hàm số: y = (m − 5)x+1 (m là tham số).

a) Tìm m để hàm số trên là hàm số bậc nhất 

b) Với giá trị nào của m thì hàm số trên đồng biến; nghịch biến trên ℝ?

Cho tam giác ABC đều tâm O. M là điểm tùy ý trong tam giác. MD, ME, MF tương ứng vuông góc với BC, CA, AB. Chọn khẳng định đúng?

Tìm số hạng thứ năm trong khai triển ${\left(x+\frac{2}{x}\right)}^{10}$ mà trong khai triển đó số mũ của x giảm dần.

Ba số hạng đầu tiên theo lũy thừa tăng dần của x trong khai triển của (1 + 2x)¹⁰ là?

Cho ∆ABC vuông tại A, AB < AC, đường cao AH. Gọi I là trung điểm của AB. Lấy điểm K đối xứng với B qua H, qua A dựng đường thẳng song song với BC cắt HI tại Da) Tứ giác AKHD là hình gì? Chứng minh?

b) CM tứ giác AHBD là hình chữ nhật. Từ đó tính diện tích tứ giác AHBD nếu AH = 6 cm, AB = 10 cm

Tập nghiệm của phương trình $\log \left(x^2-x-6\right)+x=\log \left(x+2\right)+4$ là

Tập nghiệm của phương trình ${\log }_2\left(x^2-6x+7\right)={\log }_2\left(x-3\right)$ là

cho hai đường thẳng: y = x + 3 (d₁), y = 3x + 7 (d₂).
a) Vẽ đồ thị của các hàm số đã cho trên cùng một hệ trục tọa độ Oxy.

b) Gọi giao điểm của đường thẳng (d₁) và (d₂) với trục Oy lần lượt là A và B. Tìm tọa độ trung điểm I của đoạn AB.

c) Gọi J là giao điểm của hai đường thẳng (d₁) và (d₂). Chứng minh tam giác OIJ là tam giác vuông. Tính diện tích của tam giác đó.

Cho 2 đường thẳng: $\left(d_1\right):y=\frac{1}{2}x+2$ và (d₂): y=−x+2.

Gọi A,B lần lượt là giao điểm của (d₁)và (d₂) với trục Ox, C là giao điểm của (d₁), (d₂).Tính chu vi và diện tích của tam giác ABC (đơn vị trên hệ trục tọa độ là cm).

Cho hàm số bậc nhất y=(m − 1)x+4 (d).
a) Vẽ đồ thị khi m=2.

b) Tìm m để (d) song song với đồ thị hàm số y=−3x+2(d₁).

c) Tìm m để (d) cắt đồ thị hàm số y= x −7 (d₂) tại 1 điểm nằm bên trái trục tung.

Cho hàm số bậc nhất y=(m − 1)x+4 có đồ thị là đường thẳng (d) (m là tham số và m ≠ 1).

a) Vẽ đồ thị khi m=2.

b) Với giá trị nào của m thì đường thẳng (d) song song với đường thẳng y=−3x+2(d₁).

c) Tìm m để đường thẳng (d) cắt trục Ox, Oy lần lượt tại hai điểm A, B sao cho diện tích tam giác OAB bằng 2.

ho đường tròn (O;R) và một điểm A sao cho OA = 2R, vẽ cáctiếp tuyến AB, AC với (O;R), B và C là các tiếp điểm. Vẽ đường kính BOD.

a) Chứng minh 4 điểm A, B, O, C cùng thuộc một đường tròn.

b) Chứng minh rằng: DC // OA.

c) Đường trung trực của BD cắt AC và CD lần lượt tại S và E. Chứng minhrằng OCEA là hình thang cân.

d) Gọi I là giao điểm của đoạn OA và (O), K là giao điểm của tia SI và AB.Tính theo R diện tích tứ giác AKOS.

Giải phương trình nghiệm nguyên 12x²+6xy+3y²=28(x+y)

Cho $\widehat{uOz}=30°$ và tia Ou là tia đối của tia Ov. Khi đó hai góc $\widehat{uOz};\widehat{vOz}$ được gọi là hai góc gì? Và góc $\widehat{vOz}$ bằng bao nhiêu độ?

Viết tên các cặp góc phụ nhau, bù nhau có trong hình sau:

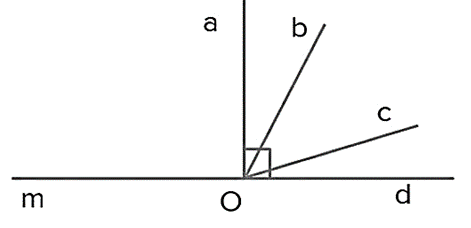
Cho a² + b² +c² = ab + bc + ca. Chứng minh a = b = c

Chứng minh bất đẳng thức: a² + b² +c² ≥ ab + bc + ca.

Cho phương trình x² − 2(m+3)x+m² − 1=0.

Tìm m để Q=x₁+x₂ − 3x₁x₂ có giá trị lớn nhất.

Cho phương trình: x² − mx+ m − 1=0(1). Tìm m để phương trình (1) có hai nghiệm phân biệt x₁ và x₂ thoả mãn: x₁² + 3x₁x₂ = 3x₂ + 3m + 16.

Tìm giá trị nhỏ nhất của biểu thức sau:A = 4x² + 4x + 11.

Tìm giá trị nhỏ nhất của A = 4x² − 4x + 11.

Giải phương trình nghiệm nguyên: x² + 2xy = 5y + 6.

Giải phương trình nghiệm nguyên: x² − 2xy + 5y² = y + 1.

Cho $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0$. Tính giá trị biểu thức $P=\frac{ab}{c^2}+\frac{bc}{a^2}+\frac{ac}{b^2}$

Chứng minh bất đẳng thức: a² + b² +c² ≥ ab + bc + ca.

Chứng minh a² + b² +c² <2(ab + bc + ca) với mọi số thực a, b, c là độ dài ba cạnh của một tam giác.

Chứng minh $\frac{a^3}{b}+\frac{b^3}{c}+\frac{c^3}{a}\ge ab+bc+ca$

Cho a, b, c > 0 thỏa a² + b² + c² = 3. CMR: $\frac{a^3{b}^3}{c}+\frac{b^3{c}^3}{a}+\frac{a^3{c}^3}{b}\ge 3abc$

Tìm x, y, z thuộc ℤ thỏa mãn: 3x² + 6y² + z² + 3y².z² − 18x = 6.

Tìm tất cả các số nguyên x, y, z thỏa mãn: 3x² + 6y² + 2z² + 3y²z² − 18 = 6

Tam giác ABC có hai đường trung tuyến BM, CN vuông góc với nhau và có BC=3, góc $\widehat{BAC}$ =30°. Tính diện tích tam giác ABC.

Cho ΔABC có AB = 4, AC = 6, $\cos \widehat{B}=\frac{1}{8}$ và $\cos \widehat{C}=\frac{3}{4}$. Tính cạnh BC.

Cho tam giác ABC có AB = 4, AC = 5, BC = 6. Tính $\cos \left(\widehat{B}+\widehat{C}\right)$

Phương trình x³ - 12x + m - 2 = 0 có 3 nghiệm phân biệt với m:

Tìm m để phương trình sau có 3 nghiệm phân biệt: x³ − 6x² + 3(m + 2)x − m − 6 = 0.

Cho điểm A nằm ngoài đường tròn (O;R). Vẽ 2 tiếp tuyến AB, AC với đường tròn (O), (B, C là các tiếp điểm). Vẽ đường kính CD của đường tròn (O).

a) Chứng minh rằng: OA $\perp$ BC và OA // BD.

b) Gọi E là giao điểm của AD và đường tròn (O) (E khác D), H là giao điểm của OA và BC. Chứng minh rằng: AE.AD = AH.AO.

Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn(B, C là các tiếp điểm).

a)Chứng minh rằng OA vuông góc với BC.

b) Vẽ đường kính CD. Chứng minh rằng BD // AO.

c)Tính độ dài các cạnh của tam giác ABC, biết OB = 2 cm; OA = 4 cm.

d) Đường thẳng AD cắt đường tròn (O) tại điểm thứ hai là M.

Chứng minh: AM.AD = AH.AO.

e) Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại E. Chứng minh ED là tiếp tuyến của đường tròn (O).

Cho hình thang cân ABCD. Đáy nhỏ AB bằng cạnh bên BC và đường chéo AC vuông góc với cạnh bên AD.

a) Tính các góc của hình thang cân.

b) Chứng minh rằng trong hình thang cân đó đáy lớn gấp đôi đáy nhỏ.

Cho hình thang ABCD có đáy lớn AD, đường chéo AC vuông góc với cạnh bên CD, $\widehat{BAC}=\widehat{CAD}$. Tính AD nếu chu vi của hình thang bằng 20 cm và góc $\widehat{D}=60°$

Chứng minh rằng x²⁰⁰² + x²⁰⁰⁰ + 1 chia hết cho x² + x + 1.

Tìm x để x² + x + 1 chia hết cho x – 1.

Cho (O; R), lấy điểm A cách O một khoảng bằng 2R. Kẻ các tiếp tuyến AB và AC với đườngtròn (B, C là các tiếp điểm). Đoạn thẳng OA cắt đường tròn (O) tại I. Đường thẳng qua O vàvuông góc với OB cắt AC tại K.
a) Chứng minh: ∆OBA vuông tại B và ∆OAK cân tại K.

b) Đường thẳng KI cắt AB tại M. Chứng minh rằng KM là tiếp tuyến của đường tròn (O).

c) Tính chu vi tam giác AMK theo R.

Cho đường tròn (O;R) và điểm A cách O một khoảng 2R. Từ A vẽ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Đường thảng vuông góc với B tại O cắt AC tại N. Đường thẳng vuông góc với OC tại O cắt AB tại M.

a) Chứng minh: AMON là hình thoi.

b) Chứng minh: MN là tiếp tuyến của đường tròn.

c) Tính diện tích AMON.

Cho đoạn thẳng AB và M là điểm nằm trên đoạn AB sao cho $AM=\frac{1}{5}AB$. Tìm k trong $\overrightarrow{MA}=k\overrightarrow{MB}$

Cho nửa đường tròn (O), đường kính AB và K là điểm chính giữa cung AB. Trên cung KB lấy một điểm M (khác K, B). Trên tia AM lấy điểm N sao cho AN = BM. Kẻ dây BP // KM. Gọi Q là giao điểm của các đường thẳng AP và BM; E là giao điểm của PB và AM.

a) Chứng minh rằng tứ giác PQME nội tiếp đường tròn.

b) Chứng minh:∆AKN= ∆BKM.

c) Chứng minh: AM . BE = AN . AQ.

d) Gọi R, S lần lượt là giao điểm thứ hai của QA, QB với đường tròn ngoại tiếp ∆OMP. Chứng minh rằng khi M di động trên cung KB thì trung điểm I của RS luôn nằm trên một đường cố định

Cho nửa đường tròn (O) đường kính AB và K là điểm chính giữa cung AB. Trên cung KB lấy một điểm M (khác K;B). Trên tia AM lấy điểm N sao cho AN =BM. Kẻ dây BP song song với KM. Gọi Q là giao điểm của các đường thẳng AP, BM.

a) So sánh hai tam giác: ΔAKN và ΔBKM.

b) Chứng minh: ΔKMN vuông cân.

c) Tứ giác ANKP là hình gì? Vì sao?

Cho tam giác ABC có $\widehat{A}={90}^{°}$, AB=AC, điểm D thuộc cạnh AB. Đường thẳng qua B và vuông góc với CD cắt đường thẳng CA ở K. Chứng minh rằng AK=AD

Cho tam giác ABC đều cạnh a và AM là trung tuyến của tam giác. Tính tích vô hướng sau: $\overrightarrow{AC}\left(2\overrightarrow{AB}-3\overrightarrow{AC}\right)$

Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng $\overrightarrow{AB}.\overrightarrow{BC}$

Gieo một con xúc xắc cân đối đồng chất hai lần. Tính xác suất để biến cố có tổng hai mặt bằng 8.

Gieo một con súc sắc cân đối đồng chất hai lần. Tính xác suất của biến cố:

a) Tổng số chấm hai mặt xuất hiện bằng 8.

b) Tích số chấm hai mặt xuất hiện là số lẻ.