5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 78)

Giải hệ phương trình:

\[\left\{ {\begin{array}{*{20}{c}}{5{a^2} + 3{b^2} = 23}\\{a + b = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD và           AB = 2CD). Gọi M là trung điểm của cạnh SC. Xác định giao tuyến của hai mặt phẳng (SAB)và (SCD).

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD và AB = 2CD). Gọi M là trung điểm của cạnh SC. Xác định giao điểm K của đường thẳng AM với (SBD).

Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông góc với nhau từng đôi một. Biết thể tích của khối chóp bằng \[\frac{{{a^3}}}{6}\]. Tính bán kính r của mặt cầu nội tiếp của hình chóp S.ABC.

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA = 2a. Gọi M là trung điểm của SD. Tính khoảng cách d giữa đường thẳng SB và mặt phẳng (ACM).

Cho tam giác ABC nhọn, vẽ đường tròn (O) đường kính BC cắt AB, AC lần lượt tại F và E; CF cắt BE tại H. Chứng minh tứ giác AEHF nội tiếp.

Cho tam giác ABC nhọn, vẽ đường tròn (O) đường kính BC cắt AB, AC lần lượt tại F và E. CF cắt BE tại H. Gọi I là tâm đường tròn ngoại tiếp tứ giác AEHF, Tính số đo cung EHF, diện tích hình quạt IEHF của đường tròn (I) nếu \[\widehat {BAC} = 60^\circ \], AH = 4 cm.

Cho tam giác ABC có \[\widehat B = 60^\circ \], BC = 8 cm, AB+AC= 12 cm. Tính độ dài AB, AC.

Cho tam giác ABC có \[\widehat B = 60^\circ \], BC = 10 cm. Chu vi của tam giác ABC là 24 cm. Tính độ dài AB, AC.

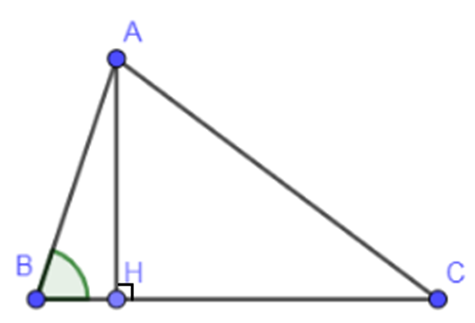
Cho tam giác ABC vuông ở A, đường cao AH. Kẻ HD vuông góc với AB và HE vuông góc với AC (D trên AB, E trên AC). Gọi O là giao điểm của AH và DE. Chứng minh AH = DE.

Cho tam giác ABC vuông ở A, đường cao AH. Kẻ HD vuông góc với AB và HE vuông góc với AC (D trên AB, E trên AC). Gọi O là giao điểm của AH và DE. Gọi P và Q lần lượt là trung điểm của BH và HC. Chứng minh tứ giác DEQP là hình thang vuông.

Cho tam giác ABC. Trên tia đối của tia AB lấy D sao cho AD = AC. Trên tia đối của AC lấy E sao cho AE = AB. Gọi M và N lần lượt là trung điểm của BE và CD. Chứng minh ΔMAC = ΔNAE.

Cho tam giác ABC. Trên tia đối của tia AB lấy D sao cho AD = AC. Trên tia đối của AC lấy E sao cho AE = AB. Gọi M và N lần lượt là trung điểm của BE và CD. Chứng minh M; A; N thẳng hàng.

Cho đường tròn (O; R), đường kính AB và tiếp tuyến Ax. Từ điểm C thuộc Ax, kẻ tiếp tuyến thứ hai CD với đường tròn (O) (D là tiếp điểm). Gọi giao điểm của CO và AD là I. Chứng minh: CO ⊥ AD.

Cho đường tròn (O; R), đường kính AB và tiếp tuyến Ax. Từ điểm C thuộc Ax, kẻ tiếp tuyến thứ hai CD với đường tròn (O) (D là tiếp điểm). Gọi giao điểm của CO và AD là I. Gọi giao điểm của CB và đường tròn (O) là E (E ≠ B). Chứng minh CE.CB = CI.CO.

Số các ước tự nhiên của 252 là bao nhiêu? Liệt kê các ước của 252.

Tìm các ước nguyên tố của 36.

Một sân chơi hình chữ nhật có chiều rộng là 28 m và chiều dài gấp 4 lần chiều rộng. người ta dùng loại gạch hình vuông có cạnh 50 cm để lát kín sân chơi đó . Hỏi cần ít nhất bao nhiêu xe gạch đủ sân chơi trên? Biết 1 chuyến chở 350 viên gạch và diện tích các mạch vữa không đáng kể.

Một mảnh đất trong công viên hình chữ nhật có chiều dài 16m và chiều rộng bằng nửa chiều dài. Người ta dự định làm một giàn hoa bên trong mảnh đất đó có hình thoi như hình bên, còn lại sẽ trồng hoa hồng nếu mỗi mét vuông trồng được 4 cây hoa hồng. Hỏi cần bao nhiêu cây hoa hồng để trồng hết phần đất còn lại?

Tìm số \[\overline {abcdef} \] (d ¹ 0) sao cho \[\overline {abcdef} = 999.\,\overline {abc} + 200\].

Cho tam giác ABC, kẻ AH ^ BC. Trên tia đối của tia HA, lấy điểm K sao cho HK = HA. Nối KB, KC. Tìm các cặp tam giác bằng nhau trong hình vẽ.

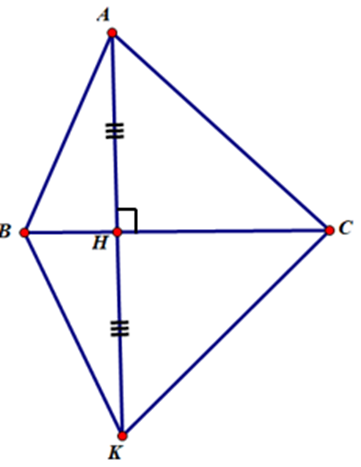
Cho tam giác ABC vuông tại A có AB < AC, đường cao AH. Trên tia đối của tia HA lấy điểm D sao cho HD = HA. Chứng minh: ΔABH = ΔDBH.

Tìm các hệ số a, b, c sao cho đa thức 3x⁴ + ax² + bx + c chia hết cho đa thức (x – 2) và chia cho đa thức (x² – 1) được thương và còn dư (−7x – 1).

Tìm a, b, c để đa thức f(x) = x³ + ax² + bx + c chia hết cho x − 2 và chia cho x² − 1 thì dư 2x.

Tìm số có 2 chữ số biết rằng nếu viết thêm chữ số 0 vào vào giữa 2 chữ số của số đó thì ta được số mới gấp 7 lần số phải tìm.

Tìm số có hai chữ số biết rằng nếu viết chữ số 3 vào giữa hai chữ số đó ta được một số có 3 chữ số gấp 11 lần số cần tìm?

Cho x + y + z = 1. Chứng minh: \[{x^2} + {y^2} + {z^2} \ge \frac{1}{3}\].

Cho (x + y + z)² = x² + y² + z².

Chứng minh rằng: \[\frac{1}{{{x^3}}} + \frac{1}{{{y^3}}} + \frac{1}{{{z^3}}} = \frac{3}{{xyz}}\]

Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.

Cho p, q là số nguyên tố và phương trình x² − px + q = 0 có nghiệm nguyên dương. Tìm p, q.

Tìm các số nguyên tố p và q sao cho 7p + q và pq + 11 cũng là các số nguyên tố.

Cho x + y = 2. Tìm giá trị nhỏ nhất của biểu thức: S = x² + y².

Cho x, y là các số dương thỏa mãn 4xy = x + y + 2. Tìm giá trị nhỏ nhất của biểu thức \[x + y + \frac{1}{{x + y}}\]

Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Chứng minh rằng OA vuông góc với BC.

Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Vẽ đường kính CD. Chứng minh rằng BD song song với AO.

Giải phương trình:\[{x^2} + 6x + 1 = (2x + 1)\sqrt {{x^2} + 2x + 3} \].

Từ các chữ số 0, 1, 2, 3, 5 có thể lập được bao nhiêu số tự nhiên không chia hết cho 5, gồm 4 chữ số khác nhau?

Từ các chữ số 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên chia hết cho 6, gồm ba chữ số đôi một khác nhau?

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA = a và SA vuông góc với đáy. Tính khoảng cách d giữa hai đường chéo nhau SC và BD.

Tìm tập hợp bội của 6.

Xác định parabol (P): y = ax² + bx + 2, biết rằng (P) đi qua hai điểm 

M (1; 5) và N (−2; 8).

Cho parabol (P): y = ax²  + bx + c có trục đối xứng là đường thẳng x = 1.  

Tính 4a + 2b.

Cho biết 3 người làm cỏ một cánh đồng hết 6 giờ. Hỏi 12 người (có cùng năng suất) làm cỏ cánh đồng đó hết bao nhiêu thời gian?

Tìm số nguyên n để n³ – 3 chia hết cho n − 2.

Tìm số nguyên n để n² + 3n + 3 chia hết cho 2n + 1.

Phân tích đa thức thành nhân tử:x³ – x²y – xy² + y³.

Phân tích đa thức thành nhân tử:–6x² – 9xy + 15y².

Tính nhanh:95,72 ´ 3,57 + 3,57 ´ 4,28

Tính nhanh: 17,8 ´ 99 + 17 + 0,8.

Trong các số sau số nào là số nguyên tố: 20; 31; 45?

Chứng minh 6 không phải là số nguyên tố.

Diện tích hình chữ nhật thay đổi như thế nào nếu: Chiều dài tăng 2 lần, chiều rộng không đổi?

Diện tích hình chữ nhật thay đổi như thế nào nếu: Chiều dài và chiều rộng tăng 3 lần?

Xác định parabol (P): y = ax²  + bx + 4 có trục đối xứng là đường thẳng \[x = \frac{1}{3}\]và đi qua điểm A(1; 3).

Cho parabol (P): y = ax²  + bx + 2. Xác định hệ số a, b biết (P) có đỉnh I(2; – 2).

Cho hàm số: y = x^-4. Tìm khẳng định sai.

Cho đường thẳng (d) có hàm số: y = (k – 3) + k' đi qua điểm A(1;2); B(– 3;4). Tìm k, k’.

Rút gọn biểu thức: \[3\sqrt 5 a - \sqrt {20} a + 4\sqrt {45} a + \sqrt a \] với a ≥ 0.

Rút gọn biểu thức: \[5\sqrt {\frac{1}{5}} + \frac{1}{{20}}\sqrt {20} + \sqrt 5 \]

Cho tứ giác ABCD, O là giao điểm của hai đường chéo AC và BD. Gọi  G; G’ theo thứ tự là trọng tâm của tam giác OAB và OCD. Biểu diễn vecto \[\overrightarrow {GG'} \].

Cho các số dương x, y, z thỏa mãn x + y + z = 1. Tìm giá trị nhỏ nhất của biểu thức: \[d(BD;SC) = OK = \frac{1}{2}d(A;SC) = \frac{1}{2} \cdot \frac{{SA.AC}}{{\sqrt {S{A^2} + A{C^2}} }}\]

Tìm giá trị nhỏ nhất của biểu thức: A = |x – 3| + |x – 5| + |x – 7|

Dựa vào tính chất liên hệ giữa thứ tự và phép cộng. Chứng minh rằng: a > b khi và chỉ khi a – b > 0.

Dựa vào tính chất liên hệ giữa thứ tự và phép cộng. Chứng minh rằng:          a + b > c khi và chỉ khi a > c – b.

Cho tam giác ABC cân tại A (AB = AC). Gọi M là trung điểm của BC. Chứng minh ΔAMB = ΔAMC.

Cho tam giác ABC cân tại A (AB = AC). Gọi M là trung điểm của BC. Qua M kẻ đường thẳng song song với AB cắt AC tại N. Chứng minh tam giác MNC cân.

Một công trường dự định phân chia số đất cho 3 đội I, II, III tỉ lệ với 7; 6; 5. Nhưng sau đó vì số người của các đội thay đổi nên đã chia tỉ lệ lại với 6; 5; 4. Như vậy có một đội là nhiều hơn 6 m² đất . Tính số đất đã phân chia cho mỗi đội.

Biết đa thức f(x) = x³ + ax² + bx + 2 chia cho x + 1 dư 5, chia cho x + 2 dư 8. Khi đó

Biết đa thức f(x) = x³ + ax + b chia cho x – 2 dư 3, chia cho x – 3 dư 5. Tìm đa thức đó.

Cho đường tròn (O; 2cm), các tiếp tuyến AB và AC kẻ từ A đến đường tròn và vuông góc với nhau tại A (B và C là các tiếp điểm). Tứ giác ABOC là hình gì? Vì sao?

Cho đường tròn (O; 2cm), các tiếp tuyến AB và AC kẻ từ A đến đường tròn và vuông góc với nhau tại A (B và C là các tiếp điểm). Gọi M là điểm bất kì thuộc cung nhỏ BC. Qua M kẻ tiếp tuyến với đường tròn, cắt AB và AC theo thứ tự tại D và E. Tính chu vi tam giác ADE.

Trong mặt phẳng Oxy cho các điểm A(–1; 2); B(5; 8). Điểm M thuộc Ox sao cho tứ giác MAB vuông tại A. Tính diện tích tam giác MAB.

Từ điểm M bên ngoài đường tròn (O) kẻ cát tuyến MAB (qua O) và tiếp tuyến MC, MD. Gọi K là giao của AC và BD. Chứng minh M,K,B,C cùng thuộc một đường tròn.

Từ điểm M bên ngoài đường tròn (O) kẻ cát tuyến MAB (qua O) và tiếp tuyến MC, MD. Gọi K là giao của AC và BD. Chứng minh MK vuông góc với AB.

Bác Kim gửi một số tiền vào ngân hàng với lãi suất là 7% và kì hạn là một năm. Sau một năm bác Kim tới ngân hàng rút cả vốn lẫn lãi được 128 400 000 đồng. Hỏi lúc đầu bác Kim gửi vào ngân hàng bao nhiêu tiền?

Bà Mai vay ngân hàng 200 triệu trong thời gian 2 năm để mở một cửa hàng chuyên sản xuất và bán quà lưu niệm. Theo hợp đồng vay vốn, lãi suất vay trong một năm là 10%. Sau 1 năm, tiền lãi của năm đầu sẽ được cộng vào vốn của năm sau. Hỏi sau 2 năm, Bà Mai phải trả ngân hàng bao nhiêu tiền?

Cho a, b, c là các số thực dương và thỏa mãn điều kiện abc = 1. Chứng minh \[\frac{1}{{2 + a}} + \frac{1}{{2 + b}} + \frac{1}{{2 + c}} \le 1\].

Cho hàm số \[y = \frac{{mx - 2m - 3}}{{x - m}}\]  với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số đồng biến trên khoảng (2; +∞). Tìm số phần tử của S.