5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 75)

Cho hình vuông ABCD, M là điểm nằm trên đoạn thẳng AC sao cho \(AM = \frac{{AC}}{4},\) N là trung điểm của đoạn thẳng DC. Tìm mệnh đề đúng?

Cho nửa đường tròn (O; R) đường kính AB. Bán kính OC vuông góc với AB. Gọi d là tiếp tuyến tại A của nửa đường tròn (O). Qua điểm M bất kì thuộc nửa đường tròn (O), kẻ tiếp tuyến với đường tròn cắt d tại E và cắt đường thẳng OC tại D. Gọi F là giao điểm của BD và d. Tiếp tuyến tại B cắt ED tại K. Chứng minh BK = EF.

Cho đa thức bậc ba P(x) thỏa mãn: P(x) chia cho x² + 2 dư 2x − 1, chia cho x² + x dư 16x − 11. Tính P(100).

Cho đa thức bậc 2 có dạng P(x) = ax² + bx + c biết rằng P(x) thỏa mãn 2 điều kiện sau: P(0) = −2 và 4P(x) – P(2x – 1) = 6x – 6. Chứng minh rằng a + b + c = 0 và xác định đa thức P(x).

Cho tam giác ABC nội tiếp đường tròn tâm O, hai đường cao BD và CE cắt nhau tại H. Vẽ đường kính AF.

a) Tứ giác BFCH là hình gì?

b) Gọi M là trung điểm của BC. Chứng minh 3 điểm H; M; F thẳng hàng.

c) Chứng minh \(OM = \frac{1}{2}AH.\)

Cho tam giác ABC, trên tia đối của tia AB lấy điểm D sao cho AD = AB. Trên tia đối của tia AC lấy điểm E sao cho AE = AC. Một đường thẳng đi qua A cắt các cạnh DE và BC theo thứ tự ở M và N. Chứng minh:

a) BC // DE.

b) AM = AN.

Cho tam giác ABC. Trên tia đối của tia AB, AC lần lượt lấy các điểm D và E sao cho AD = AB và AE = AC. Gọi M, N lần lượt là trung điểm của BC và DE. Chứng minh:

a) \[\Delta ABC = \Delta ADE\].

b) DE = BC và DE // BC.

c) \[\Delta AEN = \Delta ACM\].

d) M, A, N thẳng hàng.

Cho tam giác ABC vuông tại A có AB < AC. Vẽ AD là tia phân giác của góc BAC (D ∈ BC). Trên AC lấy điểm E sao cho AE = AB.

a) Chứng minh \(\widehat {ABD} = \widehat {AED}\).

b) Tia ED cắt AB tại F. Chứng minh AC = AF.

c) Gọi G là trung điểm của DF; AD cắt CF tại H và cắt CG tại I. Chứng minh DI = 2IH.

Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc AC, từ B kẻ tia By song song AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường thẳng MP cắt AC tại Q và đường thẳng BQ cắt AI tại H.

a) Tứ giác AMBQ là hình gì?

b) Chứng minh CH vuông góc AB.

c) Chứng minh tam giác PIQ cân.

Cho tam giác ABC vuông tại A. Gọi M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh rằng:

a) \(\Delta AMB = \Delta EMC\).

b) AC ⊥ CE.

c) BC = 2AM.

Cho tam giác ABC đều cạnh a. Gọi M, N là các điểm sao cho \(3\overrightarrow {BM} = 2\overrightarrow {BC} ,5\overrightarrow {AN} = 4\overrightarrow {AC} .\)

a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} ,\,\,\overrightarrow {BC} .\overrightarrow {AC} .\)

b) Chứng minh AM vuông góc với BN.

Từ một điểm M ở ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB đến đường tròn (A, B là hai tiếp điểm). Qua A vẽ đường thẳng song song với MB, cắt đường tròn tại E, đoạn thẳng ME cắt đường tròn tại F. Hai đường thẳng AF và MB cắt nhau tại I.

a) Chứng minh tứ giác MAOB nội tiếp đường tròn.

b) Chứng minh \(I{B^2} = IF.IA.\)

c) Chứng minh IB = IM.

Chứng minh rằng n(n + 1)(2n + 1) chia hết cho 6 với n thuộc mọi số tự nhiên.

Cúc đang làm một phép tính mà khi nhân 342 với 1 số có 2 chữ số giống nhau, Cúc đã đặt các tích riêng thẳng cột như trong phép cộng nên Cúc đã tìm ra kết quả ít hơn tích đúng là 12312. Tìm số có 2 chữ số giống nhau đó.

Chứng minh rằng với mọi số nguyên n thì n⁷ – n chia hết cho 7.

Từ một hộp chứa sáu quả cầu trắng và bốn quả cầu đen, lấy ngẫu nhiên đồng thời bốn quả, tính xác suất sao cho:

a) Bốn quả lấy ra cùng màu;

b) Có ít nhất một quả màu trắng.

Cho phương trình sau: x² + ax + b = 0. Xác định a và b để phương trình có hai nghiệm phân biệt x₁, x₂ thỏa mãn: x₁ – x₂ = 5 và \({x_1}^3 - {x_2}^3 = 35.\) Tìm 2 nghiệm phân biệt đó.

Bỏ ngoặc rồi tính: 25 – (−17) + 24 – 12.

Tìm x, y là số tự nhiên thỏa mãn phương trình \({2^x} + 3 = {y^2}.\)

Trong không gian Oxyz, cho mặt phẳng (P) : x – 2y + 2z + 6 = 0 và các điểm A(−1; 2; 3), B(3; 0; −1), C(1; 4; 7). Tìm điểm M thuộc (P) sao cho MA² + MB² + MC² đạt giá trị nhỏ nhất.

Có bao nhiêu giá trị của m để giá trị lớn nhất của hàm số y = |−x⁴ + 8x² + m| trên đoạn [−1; 3] bằng 2018?

Cho hình trụ có bán kính đáy bằng 3 và thể tích bằng 18π. Tính diện tích xung quanh S_xq của hình trụ.

Cho một đa giác đều n đỉnh, n ∈ ℕ, n ≥ 3. Tìm n biết rằng đa giác đã cho có 27 đường chéo.

Cho tam giác ABC có A(−5; 6), B(1; −3), C(−1; 1). Tìm tọa độ trung điểm H của BC.

Cho tam giác ABC vuông tại A.

a) Giả sử \(\widehat B = 54^\circ .\) Tính góc C.

b) Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm N sao cho MA = MN. Chứng minh AB // NC.

Cho tam giác ABC vuông tại A (AB < AC) và đường cao AH. Từ H kẻ HE ⊥ AB, HF ⊥ AC (E ∈ AB; F ∈ AC).

a) Chứng minh tứ giác AEHF là hình chữ nhật.

b) Gọi D là điểm đối xứng của A qua F. Chứng minh DHEF là hình bình hành.

c) Gọi I là giao điểm của EF và AH, M là trung điểm của BC. Qua A kẻ tia Ax vuông góc với đường thẳng MI cắt tia CB tại K. Chứng minh 4 điểm K, E, I, F thẳng hàng.

Cho x, y, z là 3 số thực thay đổi thỏa mãn điều kiện x + y + z = 3. Tìm giá trị nhỏ nhất của biểu thức \(P = \frac{1}{{\sqrt x }} + \frac{1}{{\sqrt y }} + \frac{1}{{\sqrt z }}.\)

Cho đường tròn (O; R) và điểm A cố định ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên d lấy M. Qua M kẻ tiếp tuyến ME, MF với (O). Nối EF cắt OM tại H, cắt OA tại B. Chứng minh:

a) Tứ giác ABHM nội tiếp.

b) OA.OB = OH.OM = R².

c) Tâm I của đường tròn nội tiếp tam giác MEF thuộc một đường tròn cố định khi M di chuyển trên d.

d) Tìm vị trí của M để diện tích tam giác HBO lớn nhất.

Cho đường tròn (O) đường kính AB. Vẽ tiếp tuyến Ax, với đường tròn (O) (A là tiếp điểm). Qua C thuộc tia Ax, vẽ đường thẳng cắt đường tròn (O) tại hai điểm D và E (D nằm giữa C và E; D và E nằm về hai phía của đường thẳng AB). Từ O vẽ OH vuông góc với đoạn thẳng DE tại H.

a) Chứng minh: tứ giác AOHC nội tiếp.

b) Chứng minh: AC.AE = AD.CE.

c) Đường thẳng CO cắt tia BD, tia BE lần lượt tại M và N. Chứng minh: AM // BN.

Làm phép tính sau: 2 357 × 24.

Giải phương trình: \(4\sqrt {x + 1} = {x^2} - 5x + 14.\)

Một mảnh đất hình chữ nhật có chiều dài là 38m, chiều rộng bằng \[\frac{3}{4}\] chiều dài, trong đó diện tích đất làm nhà chiếm 25%. Tính:

a) Diện tích của mảnh đất đó.

b) Diện tích đất làm nhà là bao nhiêu mét vuông?

Một mảnh đất hình chữ nhật có chiều dài là 40m, chiều rộng bằng \(\frac{1}{2}\) chiều dài, trong đó diện tích đất làm nhà chiếm 30%. Tính:

a) Diện tích của mảnh đất đó.

b) Diện tích đất làm nhà là bao nhiêu mét vuông?

Tìm số \(\overline {abc} \). Biết \(\overline {abc} \) chia hết cho 45 và \(\overline {abc} - \overline {cba} = 396\) (với c ≠ 0).

Cho \(\overline {abc} + \overline {\deg } \) chia hết cho 37. Chứng minh rằng \(\overline {abc\deg } \) chia hết cho 37.

Cho x, y, z > 0 và xyz = 1. CMR: \(\frac{{{x^2}}}{{\left( {1 + y} \right)}} + \frac{{{y^2}}}{{\left( {1 + z} \right)}} + \frac{{{z^2}}}{{\left( {1 + x} \right)}} \ge \frac{3}{2}\)?

Cho x, y, z > 0 và x³ + y³ + z³ = 1. Chứng minh rằng:

\[\frac{{{x^2}}}{{\sqrt {1 - {x^2}} }} + \frac{{{y^2}}}{{\sqrt {1 - {y^2}} }} + \frac{{{z^2}}}{{\sqrt {1 - {z^2}} }} \ge 2\].

Tổng tất cả các giá trị thực của tham số m để hàm số y = 3x³ + 2(m + 1)x² – 3mx + m – 5 có hai điểm cực trị x₁, x₂ đồng thời y(x₁).y(x₂) = 0 là

Tìm tập hợp tất cả các giá trị của tham số m để hàm số:

\(y = f\left( x \right) = \sqrt {{x^2} - 3mx + 4} \) có tập xác định là D = ℝ.

Để lát nền một căn phòng có dạng hình vuông có chu vi là 80 dm. Người ta phải dùng các viên gạch hình vuông để lát, mỗi viên gạch có độ dài cạnh 2 dm và có giá là 25 000 đồng/viên. Tính số viên gạch cần dùng và số tiền mua gạch để lát nền căn phòng đó.

Một khu đất hình chữ nhật có diện tích 256 m², chiều rộng là 8 m. Xung quanh khu đất người ta đóng cọc để rào xung quanh, biết rằng khoảng cách giữa hai cọc liền nhau là 4 m. Hỏi cần bao nhiêu cọc để đủ rào xung quanh khu đất đó.

Phân số thập phân thích hợp điền vào chỗ chấm:

a) 0,7% = …

b) 50% = …

Nếu gửi tiết kiệm theo kì hạn là 12 tháng thì lãi suất hàng tháng là 0,7%. Hỏi 1 người gửi 50 000 000 đồng trong 1 năm thì thu được bao nhiêu tiền lãi? (Tiền lãi của tháng không được cộng vào tiền gửi).

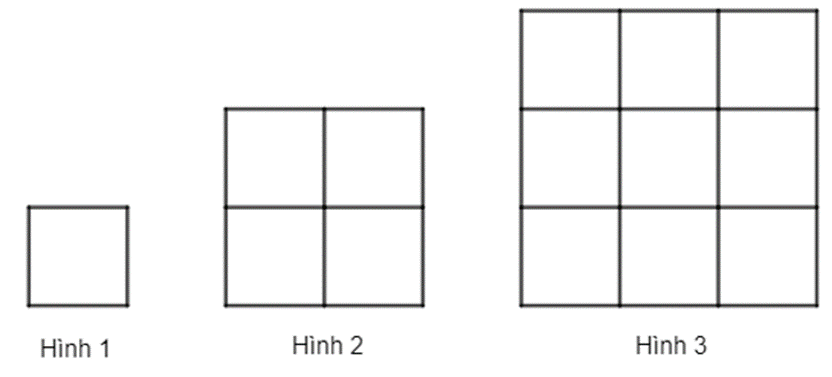
Bạn Sơn tạo các hình bằng những chiếc tăm giống nhau theo sơ đồ nhứ hình trên (Hình thứ n có n² ô vuông giống nhau và mỗi cạnh hình vuông là một chiếc tăm). Hỏi Sơn phải thêm bao nhiêu chiếc tăm vào hình thứ 2018 để được hình thứ 2019.

Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của (SAB) và (SCD) là:

Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của mp(SAD) và mp(SBC) là đường thẳng song song với đường thẳng nào trong số các đường thẳng sau?

Tính đạo hàm của hàm số sau: \(y = \sqrt {x + \sqrt {{x^2} - x + 1} } \).

Tính đạo hàm số \(y = n\left( {x + \sqrt {{x^2} + 1} } \right)\)

Tìm điểm cố định mà đường thẳng y = (m – 2)x + 3 luôn đi qua với mọi giá trị của m.

Cho hàm số y = (2m – 3)x + m – 1. Chứng minh rằng đồ thị hàm số đi qua điểm cố định với mọi giá trị của m. Tìm điểm cố định ấy.

Tìm x, biết: \(\frac{{{8^x}}}{{{2^x}}} = 4\).

Viết kết quả phép tính dưới dạng một lũy thừa.

a) 3².9³;

b) 2².5²;

c) 8⁵.2³;

d) 9⁸ : 3².

Cho △ABC nhọn các đường cao AD và BE cắt tại H. Gọi M là trung điểm BC. P đối xứng với H qua BC, Q đối xứng với H qua M.

a) PQ // BC. Tứ giác DMQP là hình gì?

b) Chứng minh rằng: HCQB là hình bình hành.

Chứng minh rằng \(\frac{{3n + 4}}{{2n + 3}}\) là phân số tối giản.

Chứng minh rằng với mọi số nguyên n thì phân số \(\frac{{{n^3} + 2n}}{{{n^4} + 3{n^2} + 1}}\) là phân số tối giản.

Cho hàm số y = mx³ – mx² – (m +4)x + 2. Xác định m để hàm số đã cho nghịch biến trên ℝ.

Cho hàm số y = x³ – (m + 1)x² – (m² – 2m)x + 2020. Tìm m để hàm số nghịch biến trên khoảng (0; 1).

Trong mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn số phức z thỏa mãn z(1 + i) là số thực là:

Trong mặt phẳng phức, tập hợp các điểm biểu diễn các số phức z thỏa mãn \(z.\overline z = 1\) là

Cho a là góc tù và \(\sin a = \frac{4}{5}\). Tính A = 2sina – cosa.

Cho hình chóp S.ABCD, đáy là hình bình hành tâm O. Gọi M, N, P, Q lần lượt là trung điểm SA, SB, SC và SD. Tìm giao tuyến của (MNPQ) và (SAC).

Cho hình chóp S.ABCD là hình bình hành tâm O. M, N, P lần lượt là trung điểm của AD, SA, SB.

a) Tìm giao tuyến của (MNP) và (SAB).

b) Tìm giao tuyến của (MNP) và (SBD).

Xác định hàm số bậc hai y = ax² + bx + c biết đồ thị của nó có đỉnh I(1; −1) và đi qua điểm A(2; 0)

Xác định hàm số bậc hai y = 2x² + bx + c biết đồ thị của nó có đỉnh I(−1; −2).

Cho tam giác ABC vuông tại A. Về phía ngoài tam giác vẽ các hình vuông ABDE, ACFG và BCHI. Ta có: