5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 74)

Tìm m để hai đồ thị hàm số y = x – 5m và y’ = 3x – m² cắt nhau tại 1 điểm có hoành độ bằng –3.

Cho hàm số bậc nhất y = (2k – 1)x + 3 – k (k là hệ số) có đồ thị là đường thẳng (d). Tìm giá trị của k để đồ thị hàm số cắt đường thẳng (d’): y = 2x + 1 tại điểm có hoành độ bằng –2.

Cho hàm số bậc nhất y = (2k – 1)x + 3 – k (k là hệ số) có đồ thị là đường thẳng (d). Tìm giá trị của k để đồ thị hàm số song song với đường thẳng (m): y = 0,5x – 3.

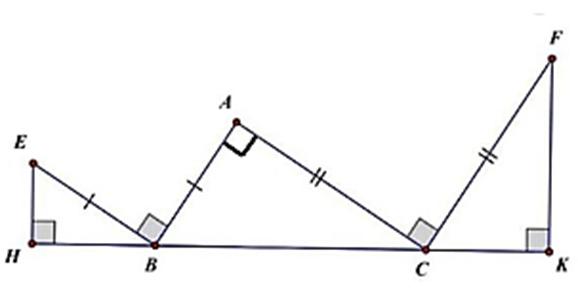
Hình vẽ bên có BE ^ BA, CF ^ CA, EH ^ BC, FK ^ BC, BE = BA và CA = CF. Chứng minh: BH = CK.

Khẳng định nào sau đây đúng?

Cho \[\,\overrightarrow u = (3;\,\, - 2),\,\,\overrightarrow v = (1;\,\,6)\]. Khẳng định nào đúng?

Trong không gian Oxyz, cho hai điểm A(2; 2; 1), \[B\left( {\frac{{ - 8}}{3};\frac{4}{3};\frac{8}{3}} \right)\]. Viết phương trình đường thẳng đi qua tâm đường tròn nội tiếp tam giác OAB và vuông góc với mặt phẳng (OAB).

Biết tổng các hệ của khai triển (x² + 1)ⁿ bằng 1024. Hãy tìm hệ số của x¹² trong khai triển trên.

Tìm hệ số của x¹²trong khai triển nhị thức Niu-tơn (2x−x²)¹⁰

Cho hệ phương trình: \[\left\{ {\begin{array}{*{20}{c}}{(m - 1)x + y = 2}\\{mx + y = m + 1}\end{array}} \right.\] với m là tham số. Chứng minh rằng với mọi giá trị của m thì hệ phương trình luôn có nghiệm duy nhất (x; y).

Cho hệ phương trình: \[\left\{ {\begin{array}{*{20}{c}}{3x - y = 2m + 3}\\{x + 2y = 3m + 1}\end{array}} \right.\] với m là tham số. Tìm m để hệ phương trình có nghiệm (x; y) thỏa mãn x² + y² = 5.

Tìm giá trị nhỏ nhất của biểu thức P = x³+y³+2x²y²biết rằng x và y là các số thực thỏa mãn điều kiện: x + y = 1.

Tìm giá trị nhỏ nhất của biểu thức P = x² + 2xy + 3y² + 5y + 10.

Phân tích đa thức thành nhân tử: x³ – 7x – 6.

Tìm x, biết: x(x − 3) + 5x = x² – 8.

Có bao nhiêu số tự nhiên có 3 chữ số dôi một khác nhau?

Từ bảy chữ số 1; 2; 3; 4; 5; 6; 7, lập các số có ba chữ số đôi một khác nhau. Có thể lập được bao nhiêu số như vậy?

Cho n điểm trên mặt phẳng. Bạn An ký hiệu chúng là A₁, A₂, ..., A_n. Bạn Bình ký hiệu chúng là B₁, B₂, ..., B_n..

Chứng minh rằng: \[\overrightarrow {{A_1}{B_1}} + \overrightarrow {{A_2}{B_2}} + ... + \overrightarrow {{A_n}{B_n}} = \overrightarrow 0 \].

Cho đường tròn (O; R) và điểm A cách O một khoảng 2R. Từ A vẽ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Đường thẳng vuông góc với OB tại O cắt AC tại N. Đường thẳng vuông góc với OC tại O cắt AB tại M. Chứng minh: AMON là hình thoi.

Cho đường tròn (O; R) và điểm A cách O một khoảng 2R. Từ A vẽ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Đường thảng vuông góc với OB tại O cắt AC tại N. Đường thẳng vuông góc với OC tại O cắt AB tại M. Chứng minh: MN là tiếp tuyến của đường tròn.

Cho a,b,c là các số dương thoả mãn ab + bc + ac = 1. Tìm giá trị nhỏ nhất của biểu thức \[P = \frac{{\sqrt {{a^2} + 1} .\sqrt {{b^2} + 1} }}{{\sqrt {{c^2} + 1} }} + \frac{{\sqrt {{b^2} + 1} .\sqrt {{c^2} + 1} }}{{\sqrt {{a^2} + 1} }} + \frac{{\sqrt {{c^2} + 1} .\sqrt {{a^2} + 1} }}{{\sqrt {{b^2} + 1} }}\].

Cho a, b, c > 0 thoả mãn \[\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = 3\]. Tìm giá trị nhỏ nhất của biểu thức:

\[P = \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}\].

Cho A(1; 2) ; B(−2; 6).  Điểm M trên trục Oy sao cho ba điểm A; B; M thẳng hàng. Tìm tọa độ điểm M.

Trong hệ tọa độ Oxy cho tam giác ABC có A(3; 5); B(1; 2) và C(5; 2). Tìm tọa độ trọng tâm G của tam giác ABC.

Cho hình bình hành ABCD, một đường thẳng d đi qua A cắt đường chéo BD tại P, cắt các đường thẳng BC và CD lần lượt là M và N. Chứng minh BM.DN không đổi.

Cho hình bình hành ABCD, một đường thẳng d đi qua A cắt đường chéo BD tại P, cắt các đường thẳng BC và CD lần lượt là M và N. Chứng minh \[\frac{1}{{AM}} + \frac{1}{{AN}} = \frac{1}{{AP}}\].

Cho hình chữ nhật ABCD (AB > BC). Từ B kẻ BH vuông góc với AC tại H. Lấy E sao cho H là trung điểm BE, lấy Q đối xứng với C qua H. Tứ giác BCEQ là hình gì? Vì sao?

Cho hình chữ nhật ABCD (AB > BC). Từ B kẻ BH vuông góc với AC tại H. Lấy E sao cho H là trung điểm BE, lấy Q đối xứng với C qua H. QE cắt DC tại M. Gọi N là hình chiếu của E trên AD, MN cắt DE tại O. Chứng minh tam giác OEM là tam giác cân.

Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DE. Gọi I, J lần lượt là trung điểm MP, NQ. Chứng minh IJ // AE và \[IJ = \frac{1}{4}AE\].

Cho nửa đường tròn (O) đường kính AB và K là điểm chính giữa cung AB. Trên cung KB lấy một điểm M (khác K; B). Trên tia AM lấy điểm N sao cho AN = BM. Kẻ dây BP song song với KM. Gọi Q là giao điểm của các đường thẳng AP, BM. So sánh hai tam giác ΔAKN và ΔBKM.

Cho nửa đường tròn (O) đường kính AB và K là điểm chính giữa cung AB. Trên cung KB lấy một điểm M (khác K; B). Trên tia AM lấy điểm N sao cho AN = BM. Kẻ dây BP song song với KM. Gọi Q là giao điểm của các đường thẳng AP, BM. Chứng minh ΔKMN vuông cân.

Cho ∆ABC và điểm M thỏa mãn\[\overrightarrow {BM} = 2\overrightarrow {CM} \]. F là một phép dời hình. Gọi A₁ = F(A), B₁ = F(B), C₁ = F(C), M₁ = F(M). Biết AB = 4, BC = 5, AC = 6. Tính độ dài đoạn A₁M₁.

Cho tam giác ABC. Các điểm D, E, H thoả mãn \[\overrightarrow {DB} = \frac{1}{3}\overrightarrow {BC} ,\,\,\,\,\overrightarrow {AE}  = \frac{1}{3}\overrightarrow {AC} ,\,\,\,\,\overrightarrow {AH} = \frac{2}{3}\overrightarrow {AB} \]. Biểu thị mỗi vecto sau \[\overrightarrow {AD} ,\,\,\overrightarrow {DH} ,\,\,\,\overrightarrow {HE} \] theo \[\overrightarrow {AB} ,\,\,\overrightarrow {AC} \].

Cho tam giác ABC. Các điểm D, E, H thoả mãn \[\overrightarrow {DB} = \frac{1}{3}\overrightarrow {BC} ,\,\,\,\,\overrightarrow {AE} = \frac{1}{3}\overrightarrow {AC} ,\,\,\,\,\overrightarrow {AH} = \frac{2}{3}\overrightarrow {AB} \]. Chứng minh D, E, H thẳng hàng.

Cho tập hợp A có n phần tử (n > 4). Biết rằng số tập con của A có 8 phần tử nhiều gấp 26 lần số tập con của A có 4 phần tử. Hãy tìm k ∈ {1; 2; 3; ...; n}sao cho số tập con gồm k phần tử của A là nhiều nhất.

Cho phương trình: x² – 4x + m = 0. Tìm m để phương trình có 2 nghiệm phân biệt x₁, x₂ thỏa mãn: x₁³ + x₂³ – 5(x₁² + x₂²) = 26.

Cho phương trình: x² – 4x + m + 1 = 0. Tìm m để phương trình có 2 nghiệm phân biệt x₁, x₂ thỏa mãn: x₁² + x₂² = 12.

Có hai xe chở xi măng, trung bình mỗi xe chở 45 bao xi măng, mỗi bao có 50 kg xi măng. Xe I chở ít hơn xe II là 6 bao xi măng. Hỏi mỗi xe chở bao nhiêu tạ xi măng?

Có 2 đoàn xe chở xi măng vào kho, đoàn xe thứ nhất có 9 xe, đoàn xe thứ hai có 7 xe. Đoàn xe thứ nhất chở nhiều hơn đoàn xe thứ hai 148 bao xi măng. Hỏi mỗi đoàn xe chở bao nhiêu bao xi măng? Biết mỗi xe chở số bao xi măng như nhau.

Có 2 vật M và N thoạt đầu cách nhau khoảng l. Cùng lúc 2 vật chuyển động thẳng đều, m chạy về B với vận tốc v₁, N chạy về C với vận tốc v₂. Tính khoảng cách ngắn nhất giữa hai vật và thời gian để đạt khoảng cách ngắn nhất giữa hai vật kể từ lúc bắt đầu chuyển động.

Mỗi ngày nhà máy làm được 125 sản phẩm. Hỏi nếu mỗi tháng nhà máy làm việc 25 ngày thì trong một năm làm được bao nhiêu sản phẩm?

Một nhà máy sản xuất trong một năm được 49410 sản phẩm. Hỏi trung bình mỗi ngày nhà máy đó sản xuất được bao nhiêu sản phẩm, biết một năm làm việc 305 ngày?

Một tấm vải dài 36 m, lần đầu người ta cắt ra 16 mảnh vải, mỗi mảnh vải dài \[1\frac{1}{5}\] m, lần thứ hai người ta cắt được 6 mảnh vải dài như nhau thì vừa hết tấm vải. Hỏi mỗi mảnh vải cắt ra ở lần 2 dài bao nhiêu mét?

Một tấm vải dài 105 m. Lần thứ nhất cắt ra \[\frac{2}{5}\] tấm vải. Lần thứ hai cắt ra \[\frac{3}{7}\]tấm vải. Hỏi tấm vải còn lại bao nhiêu mét?

Từ điểm M nằm ngoài đường tròn (O), vẽ cát tuyến MCD không đi qua tâm O và hai tiếp tuyến MA, MB đến đường tròn (O) sao cho C nằm giữa M và D. Gọi I là trung điểm của CD. Chứng minh: M, A, O, I, B cùng nằm trên 1 đường tròn.

Từ điểm M nằm ngoài đường tròn (O), vẽ cát tuyến MCD không đi qua tâm O và hai tiếp tuyến MA, MB đến đường tròn (O) sao cho C nằm giữa M và D. Gọi I là trung điểm của CD. Gọi K là giao điểm của các tiếp tuyến tại C và D của đường tròn (O). Chứng minh: A, B, K thẳng hàng.

Tìm giá trị thực của tham số m để phương trình 9^x −2.3^x+1 + m = 0 có hai nghiệm thực x₁, x₂  thỏa mãn x₁ + x₂ = 0.

Tìm các giá trị thực của tham số m để phương trình (m – 1)x² – 2mx + m = 0 có một nghiệm lớn hơn 1 và một nghiệm nhỏ hơn 1.

Tính tổng của dãy số lẻ từ 11 đến 99.

Tính tổng của dãy số chẵn từ 10 đến 50

Với những giá trị nào của m thì đồ thị các hàm số y = 2x + (3 + m) và y = 3x + (5 – m) cắt nhau tại một điểm trên trục tung?

Với giá trị nào của m thì đồ thị hàm số y = −2x + m + 2 và y = 5x + 5 – 2m cắt nhau tại một điểm trên trục tung?

Cho tập hợp A = {1; 2; 3; …; 10}. Chọn ngẫu nhiên ba số từ A. Tìm xác suất để trong ba số chọn ra không có hai số nào là hai số nguyên liên tiếp.

Giá trị lớn nhất của biểu thức A = 125 × a − b × 25 với a, b là các số có hai chữ số.

Giá trị nhỏ nhất của biểu thức A = 20 × a + b × 45 với a là các số có hai chữ số, b là số có 1 chữ số.

Một tam giác có độ dài hai cạnh là 2 cm và 10 cm. Tìm số đo của cạnh thứ ba, biết số đo ấy là một số nguyên tố.

Hãy tìm độ dài các cạnh của một tam giác, biết cạnh thứ nhất gấp 1,5 lần cạnh thứ hai, cạnh thứ hai gấp 1,5 lần cạnh thứ ba và nửa chu vi tam giác bằng         9,5 cm.

Trong 100 học sinh lớp 10, có 70 học sinh nói được tiếng Anh, 45 học sinh nói được tiếng Pháp và 23 học sinh nói được cả hai tiếng Anh và Pháp. Hỏi có bao nhiêu học sinh không nói được tiếng Anh và tiếng Pháp?

Tìm m để hai đường thẳng y = (m + 1)x – 3 và y = (2m – 1)x + 4 song song với nhau.

Tìm đường thẳng vuông góc với đường thẳng \[y = \frac{1}{3}x + 4\] và đi qua A(2; –1).

Cho hình bình hành ABCD. Lấy các điểm M, N, P thỏa mãn \[\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} ,\,\,\overrightarrow {AN} = \frac{1}{5}\overrightarrow {AC} ,\,\,\overrightarrow {AP} = \frac{1}{3}\overrightarrow {AD} \]. Đặt \[\overrightarrow {AB} = \overrightarrow a ,\,\,\overrightarrow {AD} = \overrightarrow b \]. Biểu diễn vecto \[\overrightarrow {MN} \]theo \[\vec a,\vec b\].

Cho hình bình hành ABCD. Lấy các điểm M, N, P thỏa mãn \[\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} ,\,\,\overrightarrow {AN} = \frac{1}{5}\overrightarrow {AC} ,\,\,\overrightarrow {AP} = \frac{1}{3}\overrightarrow {AD} \]. Đặt \[\overrightarrow {AB} = \overrightarrow a ,\,\,\overrightarrow {AD} = \overrightarrow b \]. Chứng minh ba điểm M, N, P thẳng hàng.

Phân tích thành nhân tử: a(a + 2b)³ − b(2a + b)³.

Phân tích thành nhân tử: ab(a − b) − ac(a + c) + bc(2a + c − b).

Lớp 5A có \[\frac{1}{5}\]số học sinh thích học Tiếng Việt, một nửa số học sinh còn laị thích học môn Toán và 12 học sinh thích học Tiếng anh. Tính số học sinh lớp 5A.

Lớp 6A có \[\frac{4}{5}\] số học sinh yêu thích môn Toán, \[\frac{7}{{10}}\] số học sinh yêu thích môn ngữ văn,\[\frac{{12}}{{25}}\] số học sinh yêu thích môn Tiếng anh. Hỏi trong 3 môn học trên môn học nào được các bạn lớp 6A thích nhất?

Tìm giá trị lớn nhất của B = –x² + 4x + 4

Phân tích đa thức thành nhân tử

x²(x² + 4) – x² + 4

0,85 viết dưới dạng tỉ số phần trăm là bao nhiêu?

Tỉ số phần trăm của 32 và 50 là bao nhiêu?

Tìm m, n nguyên dương thỏa mãn: \[\frac{1}{m} + \frac{1}{n} = \frac{1}{7}\].

Tìm m, n nguyên thỏa mãn: \[\frac{3}{m} + \frac{3}{n} = 1\]

Cho tam giác ABC cân tại A có cạnh bên bằng 6 cm và \[\widehat {BAC} = 120^\circ \]. Điểm M thuộc cạnh AB sao cho \[AM = \frac{1}{3}AB\]và N là trung điểm AC. Tính tích vô hướng \[\overrightarrow {BN} .\overrightarrow {CM} \].

Một tập hợp M có 2²⁰¹⁸ tập con. Hỏi M có bao nhiêu tập con có ít nhất 2017 phần tử? 

Tập A gồm n phần tử (n > 0). Hỏi A có bao nhiêu tập con?

Bạn Lan có một tờ giấy. Lan cắt làm đôi. Lan lại cắt làm đôi cả hai mảnh đó. Lần thứ ba Lan lại cắt đôi mỗi mảnh đã có. Hỏi cứ như thế đến lần thứ 10 Lan được bao nhiêu mảnh giấy?

Bạn Lâm có một tờ giấy màu hình chữ nhật có chiều dài 6 dm, chiều rộng 4 dm. Bạn Lâm cắt các lá cờ hình tam giác vuông có hai cạnh góc vuông là 8cm và 10 cm. Hỏi bạn Lâm cắt được bao nhiêu lá cờ như vậy? 

Cho các số: 13,1; 13,10; 1,3.10³; 1,30.10³; 1,3.10⁻³; 1,30.10⁻³. Có mấy số có hai chữ số có nghĩa.

Cho các số: 2,41; 24,1; 24,112; 2,4.10²; 2,41.10³; 2,4.10⁻⁴. Có mấy số có ba chữ số có nghĩa.

Cho góc \[\widehat {xOy}\] lấy điểm A trên Ox, điểm B trên Oy sao cho OA = OB. Gọi K là giao điểm của AB với tia phân giác của góc \[\widehat {xOy}\]. Chứng minh rằng: AK = KB.

Cho góc \[\widehat {xOy}\] lấy điểm A trên Ox, điểm B trên Oy sao cho OA = OB. Gọi K là giao điểm của AB với tia phân giác của góc \[\widehat {xOy}\]. Chứng minh rằng: OK ^ AB.