5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 61)

Một mảnh vườn có chu vi là 120 m. Chiều dài hơn chiều rộng 20 m. Tính diện tích mảnh vườn.

Một căn phòng ngủ hình chữ nhật cần lát gạch có chiều dài 8 m. Chiều rộng bằng \[\frac{3}{4}\] chiều dài. Để lát kín căn phòng đó người ta dùng loại gạch men hình vuông cạnh 4 dm. Hỏi để lát kín căn phòng người ta cần dùng bao nhiêu viên gạch?

Một căn phòng khách hình chữ nhật của nhà Mai có tỉ số giữa chiều dài và chiều rộng là \[\frac{4}{3}\]. Chiều dài hơn chiều rộng 2 m. Người ta lát nền căn phòng đó bằng loại gạch hình vuông cạnh 2 dm. Vậy để lát kín căn phòng cần bao nhiêu viên gạch?

Một viên gạch có dạng hình hộp chữ nhật có chiều dài 22 cm, chiều rộng 10 cm, chiều cao 5,5 cm. Tính diện tích xung quanh và diện tích toàn phần của khối gạch dạng hình hộp chữ nhật do 6 viên gạch xếp thành 3 hàng, mỗi hàng 2 viên.

Tính diện tích xung quanh của hình hộp chữ nhật có chiều dài 5 m, chiều rộng 3 m, chiều cao 4,5 m.

Trong một phép trừ biết tổng của số bị trừ, số trừ và hiệu bằng 7652 và hiệu số lớn hơn số trừ 798. Tìm số bị trừ, số trừ, hiệu của phép trừ đó?

Trong một phép trừ biết tổng của số bị trừ, số trừ và hiệu bằng 2000. Tìm số bị trừ và số trừ trong phép tính đó, biết rằng số trừ lớn hơn hiệu là 200.

Tìm số tự nhiên a bé nhất trong các số 1, 2, 3, 4 sao cho 3 nhân a lớn hơn 6.

Tìm số tự nhiên x bé nhất trong các số 4, 5, 6, 7, 8 sao cho 0,5 nhân x nhỏ hơn 4.

Phân tích đa thức thành nhân tử:

A = xyz + xz – yz – z + xy + x – y – 1

Tính giá trị biểu thức B với x = 11; y = 19; z = 29.

B = xyz + xz – yz – z + xy + x – y – 1.

Một ô tô trung bình mỗi giờ đi được 40 km. Hỏi trong 4 giờ ô tô đi được bao nhiêu km?

Một ô tô trung bình mỗi giờ đi được 50 km. Ô tô đi từ điểm A đến B hết 4 giờ. Hỏi quãng đường A B dài bao nhiêu km?

6 giờ 25 phút bằng bao nhiêu phút?

180 phút bằng bao nhiêu giờ?

Cho a, b, c là các số dương. Chứng minh bất đẳng thức:

\[\frac{{ab}}{{a + b}} + \frac{{bc}}{{b + c}} + \frac{{ca}}{{c + a}} \le \frac{{a + b + c}}{2}\]

Tìm giá trị lớn nhất của biểu thức: \[A = \frac{{ab}}{{a + b}} + \frac{{bc}}{{b + c}} + \frac{{ac}}{{a + c}}\].

Biết a + b + c = 6.

8 người sơn được 3 cái nhà trong 6 giờ. Hỏi với 12 người sẽ sơn được bao nhiêu cái nhà trong 12 giờ?

Cho số 650. Tìm xem số đó có chia hết cho 13 không?

Cho một số là 2,453,674. Tìm xem nó có chia hết cho 13 hay không?

Cho tam giác ABC có AB = AC. Gọi H là trung điểm của BC. Chứng minh ΔABH = ΔACH

Cho ΔABC có AB = AC. Gọi H là trung điểm của cạnh BC. Chứng minh:

a) AH là phân giác của góc \[\widehat {BAC}\].

b) AH ⊥ BC.

Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm D, E sao cho BE = BA, CD = CA. Tính \[\widehat {DAE}\].

Cho tam giác ABC (AB<AC). Trên đường thẳng chưa cạnh BC, lấy điểm D, E sao cho B nằm giữa D và C, C nằm giữa B và E, BD = BA, CE = CA. So sánh \[\widehat D\] và \[\widehat E\].

Cho tam giác ABC vuông tại A, đường cao AH. Gọi D,E lần lượt là hình chiếu của H trên AB, AC. Chứng minh rằng: AD.AB = AE.AC = HC.HB

Cho tam giác ABC vuông tại A, đường cao AM. Gọi H, K lần lượt là hình chiếu của M trên AB, AC. Biết AM = 4 cm. Tính HA.HB + KA.KC.

Cạnh thứ nhất của một hình tam giác dài 11,5 cm. Cạnh thứ nhất ngắn hơn cạnh thứ hai 0,6 cm và dài hơn cạnh thứ ba 0,9 cm. Tính chu vi hình tam giác đó.

Cạnh thứ nhất của một hình tam giác dài 5 cm. Cạnh thứ hai dài gấp 2,4 lần cạnh thứ nhất. Biết chu vi tam giác bằng 30 cm. Tính cạnh thứ ba.

Mảnh vải thứ nhất dài 2,75 m. Mảnh vải thứ hai dài gấp 3 lần mảnh vải thứ nhất và dài hơn mảnh vải thứ ba 0,86 m. Hỏi cả ba mảnh vải dài bao nhiêu mét?

Mảnh vải thứ nhất dài hơn mảnh vải thứ hai 2,7 m, biết tỉ số phần trăm giữa mảnh vải thứ hai và mảnh vải thứ nhất là 40%. Tính độ dài mỗi mảnh vải.

Một can nhựa chứa 10 lít dầu hỏa. Biết một lít dầu hỏa cân nặng 0,8 kg, can rỗng cân nặng 1,3 kg. Hỏi can dầu hỏa đó cân nặng bao nhiêu ki-lô-gam?

Một xô nhựa chứa 20 lít nước. Biết mỗi một lít nước nặng 1 kg, xô rỗng nặng 0,5 kg. Hỏi can nước đó nặng bao nhiêu kg?

Một mảnh vườn hình chữ nhật có chiều dài 24 m, chiều rộng bằng \[\frac{1}{2}\] chiều dài. Tính chu vi và diện tích của mảnh vườn đó?

Mảnh vườn hình chữ nhật có chiều rộng bằng 8 m và diện tích bằng        120 m². Tính chu vi hình chữ nhật đó.

Cho a, b, c ∈\[\mathbb{Q}\]; a, b, c đôi một khác nhau. Chứng minh rằng \[\frac{1}{{{{(a - b)}^2}}} + \frac{1}{{{{(b - c)}^2}}} + \frac{1}{{{{(c - a)}^2}}}\] bằng bình phương của một số hữu tỉ.

Số học sinh các lớp 7A, 7B, 7C, 7D lần lượt tỉ lệ với các số 11; 12; 13; 14. Biết hai lần số học sinh lớp 7B nhiều hơn số học sinh lớp 7A là 39 em. Tính số học sinh mỗi lớp.

Số học sinh lớp 7A, 7B, 7C tương ứng tỉ lệ với 21, 20, 22. Tính số học sinh của mỗi lớp. Biết rằng lớp 7C nhiều hơn lớp 7A 2 học sinh.

Trung bình cộng của 3 số là 25,42. Tổng của số thứ hai và số thứ ba là 58,5. Biết số thứ ba hơn số thứ nhất là 7,4. Tìm ba số đó.

Trung bình cộng của ba số là 13,5, biết tổng của số thứ nhất và số thứ hai là 29,1. Tổng của số thứ hai và số thứ ba là 24,7. Hãy tìm ba số đó.

Biết 3n + 10 chia hết cho 2n + 1. Tìm n.

Tìm số \[\overline {abcd} \] thoả mãn:

\[\overline {bdd,bc} - \overline {ab,cd} = \overline {a,bc} \]

Tìm số tự nhiên n sao cho 3n + 13 chia hết cho n + 1.

Tìm số tự nhiên n sao cho 5n + 19 chia hết cho 2n + 1.

Có bao nhiêu số có 4 chữ số được viết từ các chữ số 1; 2; 3; 4; 5; 6; 7; 8; 9 sao cho số đó chia hết cho 15?

Từ một điểm A ở ngoài đường tròn (O; R), kẻ hai tiếp tuyến AM và AN với đường tròn, MO cắt tia AN tại E, NO cắt tia AM tại F. Chứng minh rằng:           EF // MN.

Nhà trường tổ chức giải bóng đá mini mừng xuân cho học sinh khối lớp 8, mỗi lớp cử một đội tham dự, mỗi đội lần lượt thi đấu với đội của lớp bạn một lần.

a) Viết biểu thức đại số tính tổng số trận đấu của khối lớp 8 nếu có x (x ∈ ℤ⁺) đội tham dự.

b) Nếu tổng số trận đấu là 10 thì có bao nhiêu đội tham dự?

Chứng minh x_­² – x + 1 > 0 với mọi x.

Tìm hai số tự nhiên a, b sao cho [a, b] + (a, b) = 55.

Giải phương trình: \[\frac{{2x}}{{x - 2}} + \frac{5}{{3 - x}} = \frac{5}{{{x^2} - 5x + 6}}\]

Một lớp học có 40 học sinh chia thành các nhóm, mỗi nhóm nhiều nhất 6 học sinh. Hỏi số nhóm ít nhất có thể là bao nhiêu?

Một đội bóng có 45 cầu thủ chia thành các nhóm, mỗi nhóm nhiều nhất 11 cầu thủ. Hỏi số nhóm ít nhất có thể là bao nhiêu?

Chứng minh rằng: x³ + y³ ≥ x²y + xy²

Phân tích đa thức thành nhân tử:

x³ – x²y – xy² + y³

Một số nếu giảm đi 5 lần rồi bớt đi 32,28 thì được 41,72. Tìm số đó.

Tìm một số biết rằng nếu lấy số đó chia cho 4 rồi cộng với 9 thì được 89.

Tính bằng cách thuận tiện:

(1,1 ´ 1,2 ´ 1,3 ´ 1,4 ´ 1,5 ´ 1,6) ´ (1,25 - 0,25 ´ 5)

Tính nhanh:

a) 7,15 : 0,5 + 7,15 ´ 9 – 7,15;

b) 198 ´ 27 + 198 ´ 72 + 198.

Cho \[A = 1 + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{{63}}\]. Chứng minh rằng A > 3.

Cho \[A = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + ... + \frac{1}{{49}} - \frac{1}{{50}}\]. Chứng minh \[A < \frac{5}{6}\]

Cho hình bình hành ABCD, M và N lần lượt là trung điểm của AB và CD. Chứng minh các tứ giác AMCN là hình bình hành.

Cho hình bình hành ABCD lấy M, N lần lượt là trung điểm của AB, CD. Chứng minh rằng:

a) MN = BC

b) Ba dường thẳng AC, BD, MN đồng qui tại một điểm

Tìm x, biết:

a) (x – 2)(x – 4) = 0

b) x²(x – 3) = 0

Phân tích đa thức thành nhân tử:

a) x³ – 2x² – 5x + 6;

b) x⁴ – 16.

12 người làm xong một công việc trong 4 ngày. Hỏi 16 người làm xong công việc đó trong bao nhiêu ngày? (Biết rằng mức làm của mỗi người như nhau).

Biết 12 người làm xong một công việc trong 8 ngày. Hỏi muốn làm xong công việc đó trong 3 ngày cần bao nhiêu người? (mức làm mỗi người như nhau).

Cho biểu thức A = 1 + 3 + 3² + 3³ + 3⁴ + ….+ 3⁹⁹. Chứng minh rằng: A chia hết cho 4

Cho biểu thức B = 1 + 4 + 4² + 4³ + 4⁴ + ….+ 4⁵⁰. Chứng minh rằng: B chia hết cho 21

Cho a, b, c là các số hữu tỉ khác 0 tỏa mãn a + b + c = 0. Chứng minh rằng:

\[\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}\]là bình phương của một số hữu tỉ.

Cho a, b, c là các số hữu tỉ thảo mãn điều kiện ab + bc + ca = 1. Chứng minh rằng biểu thức Q = (a² + 1) (b² + 1) (c² + 1) là bình phương của một số hữu tỉ.

Tìm tất cả các cặp số nguyên (x; y) thảo mãn 3x² + 3xy – 17 = 7x – 2y.

Tìm cặp số nguyên (x; y) thỏa mãn phương trình:

2x² + 2xy + y² – 4x + 2y + 10 = 0.

Tính tổng \[100 - \left( {1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ... + \frac{{99}}{{100}}} \right)\]

Tìm a, b thuộc Z sao cho a.b = a +b

Tìm tất cả các cặp số nguyên thỏa mãn:

(x – 2019)² = y⁴ – 6y³ + 11y² – 6y

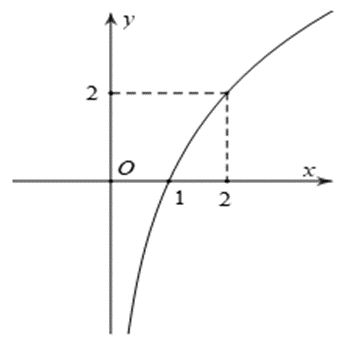
Tìm a đề hàm số y = log_ax (0 < a ¹ 1) có đồ thị là hình bên dưới:

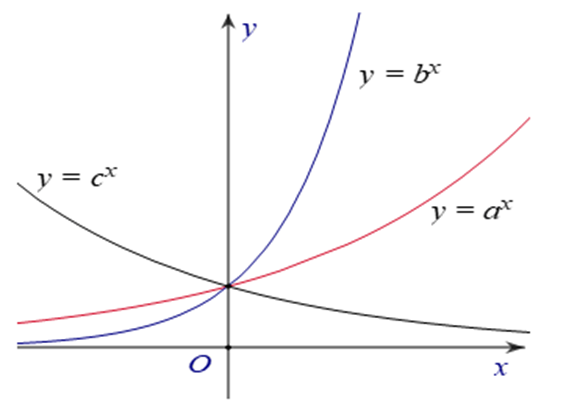
Cho đồ thị của ba hàm số y = a^x, y = b^x, y = c^x được vẽ trên cùng một hệ trục toạ độ (như hình vẽ). Chứng minh rằng b > a > c.

Số dư trong phép chia 1593,48 : 28  là bao nhiêu nếu thương là 56,9.

Cho hình vuông ABCD.Trên tia đối của tia BA lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho AE=CF. Chứng minh tam giác EDF vuông cân.

Cho hình vuông ABCD.Trên tia đối của tia BA lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho AE = CF. Gọi I là trung điểm của EF. Chứng minhBI = DI.

Tính giá trị biểu thức bằng cách nhanh nhất, biết rằng x = 3:

A = x(x – 1)(x + 2)(x – 3)(x + 4)(x – 5)

Giải phương trình: \[{x^3} - 2x + 4 = \sqrt {{x^2} + 4x + 4} \] với x > 0

Xác định số dư cảu phép chia 10051,84 : 264 (nếu thương lấy đến 2 chữ số phần thập phân).

Cho tam giác ABC cân tại A. Gọi M, N thứ tự là trung điểm của AC và AB. Gọi G là giao điểm của BM và CN. Chứng minh: ΔAMN cân.

Cho tam giác ABC cân tại A. Gọi M, N thứ tự là trung điểm của AC và AB. gọi G là giao điểm của BM và CN. Chứng minh rằng:

a) BM = CN

b) ΔGBC cân