5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 52)

Người ta trồng ngô trên một mảnh đất hình chữ nhật có chu vi là 500 m, chiều rộng kém chiều dài 50 m.

a) Tính diện tích mảnh đất đó

b) Biết rằng cứ 100 m² thu hoạch đc 30 kg ngô. Hỏi trên cả thửa ruộng thu hoạch được bao nhiêu tạ ngô?

Viết số thập phân gồm: một trăm ba mươi lăm đơn vị, hai mươi lăm phần trăm.

Cho tứ giác ABCD. Gọi E, F theo thứ tự là trung điểm của AB và CD; M, N, P, Q lầ lượt là trung điểm của các đoạn thẳng AF, CE, BF và DE. Gọi I là giao điểm của MP và EF. Chứng minh rằng:

a) I là trung điểm của MP.

b) MNPQ là hình bình hành.

Cho tam giác ABC có AB = 4, AC = 6 và \(\widehat A\)= 60°. Tính độ dài đường phân giác trong của góc A.

299 chia hết cho số nào?

Tìm các bội chung nhỏ hơn 500 của 30 và 45.

Một cửa hàng có 5 kiện hàng. Mỗi kiện hàng có 10 gói, mỗi gói có 8 sản phẩm. Hỏi trong 5 kiện hàng đó có tất cả bao nhiêu sản phẩm?

Tìm m, n biết \[\frac{{{m^2} + {n^2}}}{{10}}\,\,\, = \,\,\frac{{{m^2} - 2{n^2}}}{7}\] và m⁴n⁴ = 81.

Số 5¹⁰⁰ có bao nhiêu chữ số trong hệ thập phân?

Cho hình bình hành ABCD có AB = 8 cm, AD = 6 cm. Trên cạnh BC lấy M sao cho BM = 4 cm. Đường thẳng AM cắt đường chéo BD tại I, cắt đường thẳng DC tại N.

a) Tính tỉ số \(\frac{{IB}}{{ID}}\).

b) Chứng minh ΔMAB và ΔAND đồng dạng.

c) Tính độ dài DN và CN.

d) Chứng minh IA²  = IM.IN.

Thu gọn tổng sau A = 2 + 2² + 2³ + … + 2¹⁰⁰.

Ba bao đường cân nặng 250,7kg. Bao thứ hai và bao thứ ba cân nặng 169,8kg, bao thứ hai nhẹ hơn bao thứ nhất 5,9kg. Hỏi mỗi bao đường cân nặng bao nhiêu kg ?

Một công ty xuất nhập khẩu lần thứ nhất xuất đi được 8 tấn 700 kg cà phê lần thứ hai xuất đi được 6 tấn 300 kg. Biết rằng cứ xuất đi 5 tấn cà phê thì công ty được nhập về 500 linh kiện máy nông nghiệp. Hỏi sau hai lần xuất khẩu đó công ty được nhập về bao nhiêu linh kiện máy nông nghiệp?

Tìm phần tử thứ 1234 của dãy sau: 120, 124, 128, 132, …

Có 2 bao gạo nặng tất cả 268 kg. Nếu chuyển bớt 42 kg gạo từ bao 1 sang bao 2 thì khối lượng gạo 2 bao bằng nhau. Tính khối lượng gạo mỗi bao lúc đầu ?

2¹⁶ bằng bao nhiêu?

Số 5¹⁰⁰ có bao nhiêu chữ số trong hệ thập phân?

60 bằng mấy mũ mấy?

Viết số sau đây: Năm trăm bảy mươi sáu triệu, ba trăm ba mươi chín nghìn, tám trăm bốn mươi đồng.

Tìm a, b biết: [a; b] + (a; b) = 55.

Cho ΔABC có AB = 4cm , AC = 5cm , góc A bằng 60 độ. Tính BC.

Cho tứ giác ABCD có độ dài 4 cạnh là a, b, c, d, diện tích là S.

Chứng minh S ≤ \[\frac{{{a^2} + \,{b^2} + {c^2} + {d^2}}}{4}\].

Tìm số có 2 chữ số có tổng của 2 chữ số đó bằng 17. Nếu đổi chỗ hai chữ số đó cho nhau thì ta được số bé kém số đó 9 đơn vị.

Có 2 bao gạo nặng tất cả 268 kg. Nếu chuyển bớt 42 kg gạo từ bao 1 sang bao 2 thì khối lượng gạo 2 bao bằng nhau. Tính khối lượng gạo mỗi bao lúc đầu ?

Hình tròn có bán kính 6 cm thì sẽ có đường kính 12 cm đúng hay sai?

Lớp 5A và 5B trồng được 78 cây. Biết rằng nếu lớp 5A trồng thêm được 6 cây nữa thì sẽ trồng gấp đôi lớp 5B. Hỏi mỗi lớp trồng được bao nhiêu cây?

Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy C₁, A₁, B₁ sao cho các đường thẳng AA₁, BB₁, CC₁ đồng quy tại O. Đường thẳng qua O // AC cắt A₁B₁, B₁C₁, tại K và M tương ứng. Chứng minh rằng: OK = OM.

Trong một phép nhân, thừa số thứ nhất tăng lên 7 đơn vị thì tích tăng 21 đơn vị. Hỏi thừa số thứ hai bằng bao nhiêu?

Tìm hai số a, b biết 7a = 11b và (a; b) = 45.

Tính diện tích của mảnh đất có kích thước theo hình vẽ bên (được tạo bởi hình chữ nhật ABCD và hình vuông CEMN cạnh bằng 7 m).

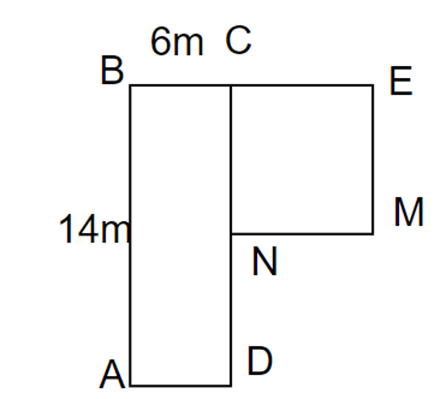
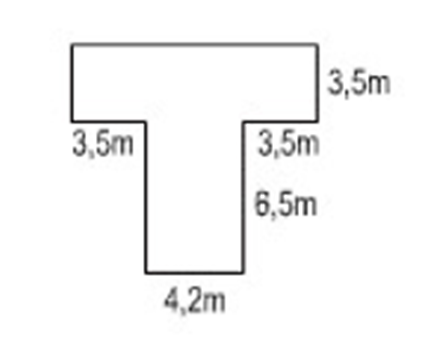
Tính diện tích của mảnh đất có kích thước theo hình vẽ bên.

Tính tổng số lẻ liên tiếp từ 15 đến 155.

Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ta có thể lập được bao nhiêu số tự nhiên có 4 chữ số khác nhau và chia hết cho 3?

Cho b² = ac. Chứng minh \[\frac{a}{c}\,\, = \,\,\frac{{{a^2} + \,{b^2}}}{{{c^2} + {b^2}}}\] (giả sử các biểu thức đều có nghĩa).

Cho x = \(1 + \sqrt[3]{2} + \sqrt[3]{4}\). Chứng minh rằng P = x³ – 3x² – 3x + 3 là một số chính phương.

Xe tải nhỏ chở được 2345 tấn hàng và chở ít hơn xe tải to 2325 tấn hàng. Hỏi cả hai xe chở được bao nhiêu tấn hàng?

Chứng minh rằng \(\left| a \right| + \left| b \right|\, \ge \,\left| {a + b} \right|\) với mọi a, b ∈ ℝ.

Tìm Ư(25).

Phân tích đa thức thành nhân tử: 5x² – 25x – 120.

Tìm số tự nhiên a nhỏ nhất khác 0, biết rằng a chia hết cho 15 và a chia hết cho 12.

Cho \(\frac{a}{b}\,\, = \,\,\frac{c}{d}\). Các số x, y, z, t thỏa mãn xa + yb ≠ 0 và zc + td ≠ 0.

Chứng minh: \(\frac{{xa + yb}}{{za + tb}}\,\, = \,\,\frac{{xc + yd}}{{zc + td}}\).

Để đánh số trang của cuốn sách, người ra phải dùng 936 lượt chữ. Hỏi cuốn sách đó có bao nhiêu trang?

Khi nhân một số với 7254, Mai đã viết nhầm chữ số 4 ở hàng đơn vị của số 7254 thành chữ số 8 nên tích tăng thêm 20 đơn vị. Hãy tìm tích đúng của phép nhân đó.

Một thùng đựng 100 hộp bút chì màu, mỗi hộp có 6 bút chì. Hỏi 9 thùng có bao nhiêu bút chì màu?

Tìm số trung bình cộng của dãy số gồm các số lẻ từ 11 đến 100

Tam giác ABC có góc A bằng 90°, AB = 12 cm, AC =16 cm; đường phân giác góc A cắt BC tại D.

a) Tính BC, BD và DC.

b) Kẻ đường cao AH, tính AH, HD, AD.

Giải phương trình: \[\left( {\frac{1}{2}} \right)3{x^2} = \frac{1}{{256}}\].

Tính đạo hàm của hàm số: y = \[\frac{3}{{{{\left( {2x - 5} \right)}^2}}}\].

Cho tam giác ABC. Gọi M là trung điểm của AB và N là một điểm trên cạnh AC sao cho NA = 2NC. Gọi K là trung điểm của MN. Phân tích \(\overrightarrow {AK} \,theo\,\overrightarrow {AB} ,\,\overrightarrow {AC} \).

Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F. Chứng minh BE² + CF² ≥ EF², khi nào dấu “=” xảy ra?

Hệ số của x trong phép nhân\[\left( {{x^2} - \frac{1}{2}} \right)\left( {{x^2} - 4} \right)\].

Một khu đất hình chữ nhật có chu vi là 0,45km. Chiều rộng bằng \[\frac{4}{5}\]chiều dài. Tính diện tích khu đất với đơn vị đo là mét vuông, héc – ta.

Với 3^x–2 = 27. Giá trị của x là?

Tìm 1 + 2 + 3 + …. + x = 1275.

Với 3^x–2 = 27. Giá trị của x là?

Cho tam giác ABC vuông tại A, đường cao AH = 2,5 cm, BC = 5 cm. Tính AC, AB.

Tìm BCNN của (42, 35, 180).

Một tổ có 8 học sinh. Có bao nhiêu cách chọn 3 bạn để làm các công việc trực nhật: quét lớp, lau bảng, đổ rác (mỗi bạn làm một công việc)?

Rút gọn biểu thức: A = \(\frac{{2{x^3} - 3{x^2} + 3x - 1}}{{{x^2} - x + 1}}\).

Tính A = 1 + 2² + 2³ + … + 2¹⁰⁰.

Tính bằng cách hợp lý: A = 100 + 98 + 96 + … + 2 – 99 – 97 – … – 1.

Tìm số tự nhiên x biết rằng 126 ⋮ x; 210 ⋮ x và 15 < x < 30.

Tính A = 2022 + 2020 + 2018 + 2016 + …. + 2 – 2019 – 2017 – 2015 – … – 1.

Tìm x biết 60 chia hết x , 150 chia hết x và x > 25.

Giả sử ABC là tam giác nhọn nội tiếp đường tròn (O). Đường cao AH cắt đường tròn (O) tại D. Kẻ đường kính AE của đường tròn (O). Chứng minh:

a, BC song song với DE.

b, Tứ giác BCED là hình thang cân.

1 đường thẳng chia mặt phẳng làm 2 miền. Hỏi 2 đường thẳng chia mặt phẳng làm mấy miền?

Cho hình thang OABC, M, N lần lượt là trung điểm của OB và OC. Chứng minh rằng: \[\overrightarrow {AM} = \frac{1}{2}\overrightarrow {OB} - \overrightarrow {OA} \]và  \[\overrightarrow {MN} = \frac{1}{2}\left( {\overrightarrow {OC} - \overrightarrow {OB} \,} \right)\].

Cho tam giác AB < AC. Tia phân giác của góc A cắt đường trung trực của BC tại I. kẻ IH vuông góc với đường thẳng AB, kẻ IK vuông góc với đường thẳng AC. Chứng minh rằng BH = CK.

Cho tam giác AB < AC. Tia phân giác của góc A cắt đường trung trực của BC tại I. kẻ IH vuông góc với đường thẳng AB, kẻ IK vuông góc với đường thẳng AC. Chứng minh rằng BH = CK.

Cho tam giác ABC vuông tại A, đường cao AH.

Chứng minh rằng: S_BHD = \(\frac{1}{4}\)S_BKC cos²ABD.

Cho tam giác ABC vuông tại A, đường cao AH. Gọi M và N lần lượt là trung điểm của AH và CH. Chứng minh M là trực tâm của tam giác ANB.

Tính chu vi hình vuông biết diện tích hình vuông là 169 dm².

Tính chu vi hình vuông biết diện tích hình vuông là 49 cm².

Một cửa hàng có 3 bao gạo nếp mỗi bao cân nặng 36kg và 6 bao gạo tẻ mỗi bao cân nặng 54 kg. Trung bình mỗi bao cân nặng là bao nhiêu?

Một phép chia có số chia là 5, số dư là 1. Để phép chia là phép chia hết thì cần thêm vào số bị chia bao nhiêu đơn vị?

Một thửa ruộng hình chữ nhật có chiều rộng là 80m, chiều dài bằng \(\frac{5}{4}\) chiều rộng.

a) Tính diện tích thửa ruộng đó.

b) Biết rằng trung bình cứ 50m²  thu hoạch được 30 kg thóc. Hỏi trên cả thửa ruộng đó người ta thu hoạch được bao nhiêu tạ thóc ?

Người thợ may lấy ra một tấm vải dài để cắt may 4 bộ quần áo, mỗi áo hết 300 cm và mỗi quần hết 325 cm. Sau khi cắt xong thì tấm vải còn lại dài 2 m. Hỏi tấm vải ban đầu vải dài bao nhiêu cm?

72 có bao nhiêu ước?

Rút gọn phân thức sau: \(\frac{{14{x^5}{y^3}{z^2}}}{{21{x^2}{y^4}z}}\).

Đại lượng y tỉ lệ nghịch với đại lượng x theo hệ số tỉ lệ a thì đại lượng x tỉ lệ nghịch với đại lượng y theo hệ số tỉ lệ là?

Cho nửa đường tròn (O) đường kính AB. Gọi E là 1 điểm nằm ngoài đường tròn. Tia AE và tia BE cắt đường tròn (O) tại C và D. AD cắt BC tại H.

a) Chứng minh: \(\widehat {AEH} = \widehat {ABH}\).

b) Biết \[\widehat {EAB}\]= 75° và \(\widehat {EBA}\)= 55°. Tính \(\widehat {COD}\).

Cho tam giác ABC có AC = 2AB, đường trung tuyến BM . Gọi H là chân đường vuông góc kẻ từ C đến tia phân giác của góc A. Chứng minh rằng ABHM là hình thoi.

Chứng minh rằng với x, y thuộc Z thì A = xy (x⁴ – y⁴) chia hết cho 5.

Một trường THCS xếp hàng 20,25,30 đều dư 13 nhưng xếp hàng 45 còn thừa 28 học sinh. Tính số học sinh của trường đó biết rằng số học sinh chưa tới 1000.

Số 243 có bao nhiêu ước tự nhiên?

Tính các góc của tam giác ABC biết \(3\widehat A = 4\widehat B\) và \(\widehat A - \widehat B\)= 20°.

Một thư viện trường học có 8 giá sách lớn và 9 giá sách nhỏ, mỗi giá sách lớn để 875 cuốn sách, mỗi giá sách nhỏ để 375 cuốn sách. Hỏi thư viện đó có tất cả bao nhiêu cuốn sách?

Tính C = 1.2 + 2.3 + 3.4 +….+ n(n + 1).

Bạn Nam xếp lên bảng số có 4 chữ số 7839. Nam đố Bình xóa đi một chữ số trong số đã cho và xếp lại thứ tự cho các chữ số còn lại. Số lớn nhất Bình có thể xếp được là?

Cho hình bình hành ABCD. gọi O là giao điểm hai đường chéo AC và BD. Đường thẳng qua O không song song với AD cắt AB tại M và CD tại N.

a) Chứng minh M đối xứng với N qua O.

b) Chứng tỏ rằng tứ giác AMCN là hình bình hành.

Cho hình bình hành ABCD. Gọi O là giao điểm 2 đường chéo AC và BD. Qua O vẽ đường thẳng a cắt AD, BC lần lượt tại E, F. qua O vẽ đường thẳng b cắt AB và CD lần lượt tại K, H. Chứng minh tứ giác EKFH là hình bình hành.

Mua 3 túi xà phòng và 2m vải thì hết 64 000 đồng. Nếu mua 2 túi xà phòng và 3m vải như vậy thì hết 71 000 đồng. Tính giá tiền 1 túi xà phòng và 1m vải?

Tìm các ước của 480.

Một mảnh đất hình chữ nhật có chiều dài 4,5 m. Chiều rộng bằng \(\frac{3}{4}\) chiều dài Tính diện tích mảnh đất đó dưới dạng số thập phân.

Cho hình chữ nhật ABCD có diện tích bằng 48 cm²; MC = MD; BN = \(\frac{2}{3}\)BC. Tính diện tích tam giác AMN.

Một phép nhân có thừa số thứ 2 là 45. Nếu viết các tích riêng thẳng cột như trong phép cộng thì tích đúng bị giảm đi 828 đơn vị. Tìm tích đúng.

Rút gọn biểu thức: 13x⁴ – 9x² – 21(6x²²⁸).

Hãy tìm số nguyên tố p sao cho 3p + 5 là số nguyên tố.

Một khu rừng hình chữ nhật có chu vi 5 km 60 dam. Chiều dài hơn chiều rộng 800 m.

a) Hỏi diện tích khu rừng đó bằng bao nhiêu ha? Bao nhiêu m²?

b) Biết \(\frac{1}{3}\) diện tích khu rừng trồng cây mới. Tính tỉ số diện tích trồng cây mới và phần diện tích còn lại của khu rừng.

Tìm hai chữ số tận cùng của 5ⁿ (n lớn hơn 1).

Tìm a, b nguyên biết: a³ – 3ab² = 1 – 3a²b và b³ = 1

Rút gọn A = 1 + \(\frac{1}{2} + {\left( {\frac{1}{2}} \right)^2} + {\left( {\frac{1}{2}} \right)^3} + .... + {\left( {\frac{1}{2}} \right)^{2012}}\).

Tìm x, y nguyên biết xy + 3x – y = 6.

Tìm chữ số tận cùng của \({234^{{5^{{6^7}}}}}\).

Tìm điều kiện xác định của x để biểu thức có nghĩa: \(\sqrt {\frac{{3x - 2}}{{{x^2} - 2x + 4}}} \).

Giải phương trình: x² + \(\left( {3 - \sqrt {{x^2} + 2} } \right)\)x = 1 + 2\(\sqrt {{x^2} + 2} \).

Hãy cho biết: a³ b³c³ = (abc)³ không?

Chứng minh rằng trong tam giác ABC ta có hệ thức: sin A = sinB. cosC + sinC. cosB.

Cửa hàng buổi sáng bán được 45 kg gạo, buổi chiều bán được 40 kg gạo. Buổi tối bán kém hơn mức trung bình cả ba buổi là 3 kg gạo. Hỏi buổi tối bán được bao nhiêu kg gạo?

147 có là lũy thừa của số nào không?

Tìm tập hợp các số tự nhiên a sao cho 2a + 31 là bội của a + 1.

Tìm số tự nhiên x biết 450 < x < 700 và x chia hết cho 20, 25, 30.

Điền vào chỗ trống: 48 dm² = …m².

Điền vào chỗ trống: 50200 cm² =. . . m² = . . . dm².

Khử mẫu biểu thức lấy căn: \[\frac{{59}}{{\sqrt 3 + \sqrt 5 + \sqrt 7 }}\].

Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh rằng: AH = BC. sin B. cos B.

Trong một phép chia có thương bằng \(\frac{1}{8}\) số bị chia. Thương gấp 3 lần số chia. Tìm số bị chia.

Hùng và Dũng có tất cả 45 viên bi. Nếu Hùng có thêm 5 viên bi thì Hùng có nhiều hơn Dũng 14 viên. Hỏi lúc đầu mỗi bạn có bao nhiêu viên bi?

Cho 2 số thập phân 14,78 và 1,87. Hãy tìm số A sao cho thêm A vào số nhỏ, bớt A ở số lớn ta được 2 số có tỉ số là \(\frac{1}{4}\).

Cho hình chữ nhật ABCD có diện tích bằng 48 cm²; MC = MD; BN = \(\frac{2}{3}\) BC. Tính diện tích tam giác AMN.

Cho hình thang ABCD; MA = MC ; MN song song BD. Giải thích tại sao BN chia hình thang thành 2 phần có diện tích bằng nhau.

Cho hình vuông ABCD cạnh a, điểm N trên cạnh AB, tia CN cắt tia DA tại E: tia Cx vuông góc với tia CE, tia Cx cắt AB tại F. Gọi M là trung điểm của đoạn EF.  

a) CE = CF và M, B, D thẳng hàng. 

b) Chứng minh \(\widehat {ACE}\,\, = \,\,\widehat {BCM}\).

Cho hình vẽ dưới đây, biết các hình vuông ACDB và EGFD có cạnh là 3 cm và 5 cm. Tính diện tích phần tô đậm?

Cho một phép chia có thương bằng 11. tìm số bị chia biết rằng nếu ta giảm thương đi 3 đơn vị thì số bị chia giảm 195 đơn vị.

Cho tam giác ABC gọi M,N,P lần lượt là trung điểm của 3 cạnh AB,AC,BC. Gọi I là giao điểm AP và MN. Chứng minh I là trung điểm MN.

Cho tam giác ABC thỏa mãn sin²a = sin²b + sin²c. Chứng minh rằng tam giác ABC vuông. Biết AB = c; AC = b; BC = a.

Cho hai đường tròn  (O ; R) và (O' ; r) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, B ∈ (O), C ∈ (O'). Tính \(\widehat {BAC}\).

Chứng tỏ rằng \(\overline {abcabc} \) là bội của 7, 11 và 13.