5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 49)

Cho nửa đường tròn (O) đường kính AB, C thuộc cung AB (CA < CB). Vẽ dây BE song song với OC. Chứng minh CA = CE.

Cho tam giác ABC, D là trung điểm của AC, E là trung điểm của AB. Trên tia đối của DB lấy điểm N sao cho DN = DB. Trên tia đối của tia EC lấy điểm M sao cho EM = EC. Chứng minh rằng A là trung điểm của MN.

Cho tam giác ABC, D là trung điểm của AC, E là trung điểm của AB. Trên tia đối của DB lấy điểm N sao cho DN = DB. Trên tia đối của tia EC lấy điểm M sao cho EM = EC.

a) Chứng minh DCDN = DADB.

b) Chứng minh AM // BC.

c) Chứng minh rằng A là trung điểm của MN.

Cho đường tròn (O; R) và dây\[AB = \frac{8}{5}R\]. Vẽ một tiếp tuyến song song vói AB, cắt các tia OA, OB lần lượt tại M và N. Tính diện tích tam giác OMN.

Cho đường thẳng d: y = (2m + 1).x - 2 và \[m \ne \frac{1}{2}\]. Giả sử d cắt Ox tại A, cắt Oy tại B. Tìm m để \[{S_{OAB}} = \frac{1}{2}\].

Cho hàm số y = (m² – 2m + 3)x + 6m có đồ thị là (d). Giá trị của m để (d) cắt Ox tại A, cắt Oy tại B sao cho S_OAB lớn nhất.

Cho tam giác ABC. Các đường cao AD, BE, CK (D, E, K tương ứng thuộc các cạnh BC, CA, AB) gọi là các đường n – tuyến của DABC nếu như: \[\frac{{BD}}{{BC}} = \frac{{CE}}{{CA}} = \frac{{AK}}{{AB}} = \frac{1}{n}\](n là số dương cho trước). Đặt AD = d_a, BE = d_b, CK = d_c (và gọi d_a, d_b, d_c là độ dài của các đường n - tuyến). Chứng minh rằng:

d_a² + d_b² + d_c² = \[\frac{{{n^2} - n + 1}}{n}\left( {{a^2} + {b^2} + {c^2}} \right)\].

12 người làm xong một công việc trong 4 ngày. Hỏi 16 người làm xong công việc đó trong bao nhiêu ngày ? (Mức làm của mỗi người như nhau).

Chứng minh rằng tích 3 số tự nhiên chia hết cho 6.

Chứng minh rằng tích của 3 số tự nhiên liên tiếp chia hết cho 6.

Tìm hiệu của 2 số biết rằng nếu số bị trừ bớt đi 735 đơn vị và thêm vào số bị trừ 265 đơn vị thì hiệu mới bằng 12 000.

Cho \[M = \frac{{{a^2} + {b^2} + {c^2}}}{{2ab}} + \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} + \frac{{{c^2} + {a^2} - {b^2}}}{{2ac}}\]. Chứng minh rằng:

a) Nếu a, b, c là độ dài 3 cạnh của một tam giác thì M < 1.

b) Nếu M = 1 thì hai trong ba phân thức đã cho của M = 1, phân thức còn lại bằng -1.

Cho tam giác ABC có \[\widehat A = 60^\circ \], AB = 6, AC = 9. Tính diện tích S và đường cao AH của tam giác ABC.

Cho tam giác ABC, biết \[\widehat B = 60^\circ \], AB = 6 cm, BC = 4 cm. Tính độ dài cạnh AC.

Cho A = n⁶ + 10n⁴ + n³ + 98n - 6n⁵ - 26 và B = 1 + n³ - n.

Chứng minh mọi n Îℤ thì thương của phép chia a cho b là bội của 6.

Cho A = n⁶ + 10n⁴ + n³ + 98n - 6n⁵ - 26 và B = 1 + n³ - n.

Chứng minh mọi n Î ℤ thì thương của phép chia a cho b là bội của 6.

Cho các số sau: 99; 33; 57; 72; 2019; 8820; 1739; 639; 1392.

a) Số nào chia hết cho 9?

b) Số nào không chia hết cho 9?

Tìm số tự nhiên có bốn chữ số chia hết cho 5 và cho 27 biết rằng hai chữ số giữa của số đó là 97.

Tìm một phân số có tổng của tử số và mẫu số bằng 175 và biết nếu thêm 9 đơn vị vào tử số của phân số đó ta được phân số mới bằng 1.

Một hình chữ nhật có chu vi là 24cm, có chiều dài hơn chiều rộng 2cm. Tính diện tích hình chữ nhật đó?

Một hình chữ nhật có chu vi là 24cm, chiều dài gấp 3 lần chiều rộng. Tìm diện tích của hình chữ nhật đó?

Cho tam giác ABC vuông tại A có AB = 8, AC = 15, BC = 17. Tính độ dài đường trung tuyến AM.

Tam giác ABC vuông tại A và có AB = AC = a. Tính độ dài đường trung tuyến BM của tam giác đã cho.

Một liên đội thiếu niên khi xếp hàng 2, hàng 3, hàng 4, hàng 5 đều thừa 1 người. Tính số đội của liên đội biết rằng số đội viên khoảng từ 100 đến 150 ?

Tìm hai số nguyên tố biết tổng của chúng bằng 139.

Viết số thập phân thích hợp:

2 giờ 15 phút = ... giờ     

1 giờ 45 phút = ... giờ     

4 giờ 54 phút = ... giờ

3 giờ 36 phút = ... giờ

Viết số thập phân thích hợp vào chỗ chấm:

15 phút = ... giờ

84 phút = ... giờ

360 giây = ... giờ

426 giây = ... phút

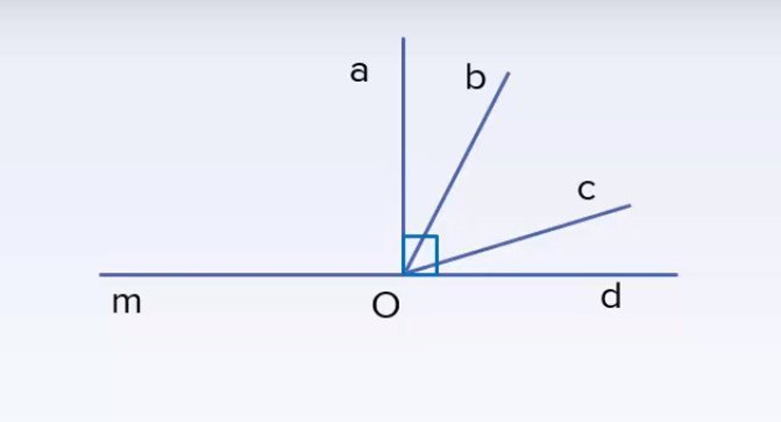
Viết tên các cặp góc phụ nhau, bù nhau có trong hình sau

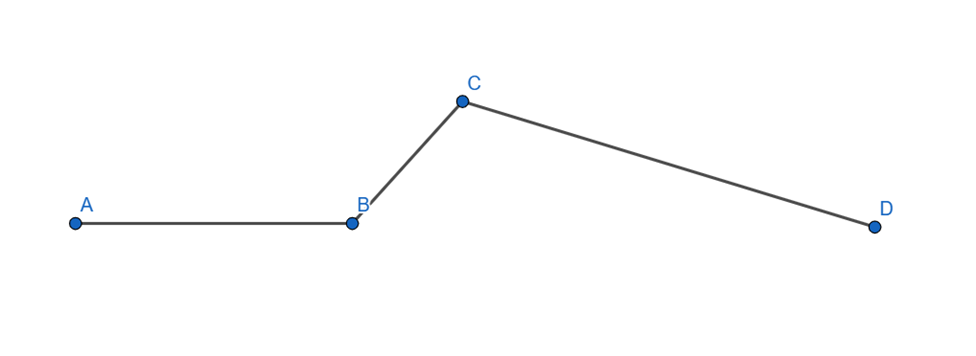
Cho đường gấp khúc ABCD, biết đoạn thẳng \[AB = \frac{1}{2}BC\]và AB = 3 cm. Độ dài đường gấp khúc BCD dài hơn độ dài đường gấp khúc ABC là 5 cm. Tính độ dài đường gấp khúc ABCD.

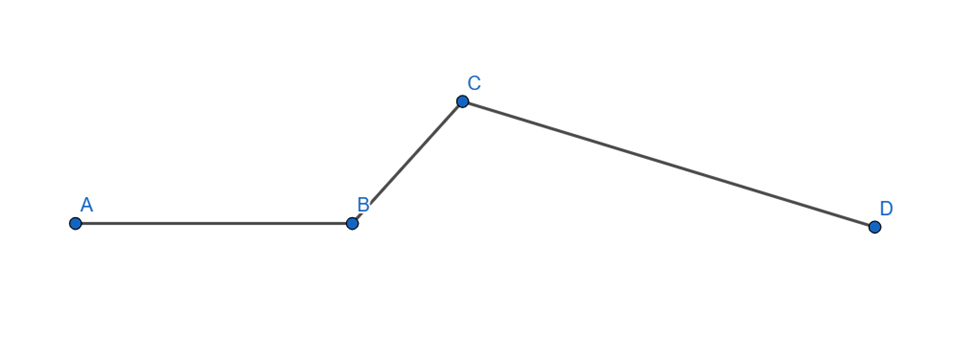
Có đường gấp khúc ABCD, có AB = 15 cm. Biết đường gấp khúc ABC dài hơn đường gấp khúc BCD là 3 cm. Tính độ dài đường gấp khúc CD.

Bất phương trình \[\left| {x - 5} \right| \le 4\] có bao nhiêu nghiệm nguyên ?

Số nghiệm nguyên của bất phương trình 2x² - 3x - 15 £ 0 là

Có 50 chai sữa, mỗi chai có 0,5l sữa. Mỗi lít sữa cân nặng 1,02kg. Mỗi vỏ chai cân nặng 0,2kg. Hỏi 50 chai sữa đó cân nặng tất cả bao nhiêu kg?

Giải phương trình sau: (3.x - 2⁴).7³ = 2.7⁴.

Viết 729 dưới dạng luỹ thừa với ba cơ số khác nhau và số mũ lớn hơn 1.

Có 20 chai sữa, mỗi chai chứa 0,75 lít sữa. Mỗi lít sữa can nặng 1,04 kg. Mỗi vỏ chai cân nặng 0,25 kg. Hỏi 20 chai sữa đó cân nặng bao nhiêu ki- lô- gam?

Giải phương trình: 4^x + 3^{2x + 1} = 3.18^x + 2^x.

Tổng các nghiệm của phương trình 4^x + 3^{(2x + 1)} = 3.18^x + 2^x.

Giải phương trình \[\sqrt {2x + 1} = 7 - x\].

Trong kì thi học sinh giỏi cấp trường, lớp 10A có 17 bạn được công nhận học sinh giỏi Văn, có 25 bạn được công nhận học sinh giỏi Toán. Biết cả lớp 10A có 45 học sinh và 13 học sinh không đạt học sinh giỏi. Số học sinh giỏi cả văn lẫn toán là

Tìm các số tự nhiên a, b thoả mãn 2a² + b² + 2ab + 2a - 4b < 0.

Khi chia số tự nhiên a cho 36, ta được số dư là 12. Hỏi a có chia hết cho 4 không? Có chia hết cho 9 không? Giải thích.

May một bộ quần áo hết 2,8 m vải hỏi có 371,5 m vải thì may được nhiều nhất bao nhiêu bộ quần áo như thế và còn thừa mấy mét vải?

Khi chia số tự nhiên a cho 54, ta được số dư là 38. Khi chia a cho 18 ta được thương là 14 và còn dư. Tìm số a.

Tìm x, biết: 2^{x + 1} – 2^x = 32.

Tìm x, biết: 2^{x + 1} – 2^x = 32.

Tính tổng của các số tự nhiên x, biết x là số có 2 chữ số và 12 < x < 91.

Trong dịp tết nguyên đán một cửa hàng đã chuẩn bị một số hộp mứt đủ bán trong 20 ngày, nếu mỗi ngày bán 320 hộp, nhưng thực tế cửa hàng bán một ngày 400 hộp. Hỏi số hộp mứt cửa hàng đã chuẩn bị đủ bán được bao nhiêu ngày?

Từ 2 đến 20 có bao nhiêu số ...

a) chia hết cho 2;

b) chia hết cho 5;

c) chia hết cho 3;

d) chia hết cho 9.

Giải phương trình 2^{x + 2} - 2^x = 96.

Tính C = 3 + 3² + 3³ + ... + 3^{1 000}.

Một căn phòng hình chữ nhật có chiều dài 8m, chiều rộng bằng \[\frac{3}{4}\]chiều dài, để lát nền căn phòng đó người ta dùng loại gạch men vuông có cạnh 4dm. Hỏi căn phòng được lát nền bằng bao nhiêu gạch men đó? ( biết phần diện tích mạch vữa không đáng kể).

Một căn phòng hình chữ nhật có chiều dài 8m, chiều rộng 6m. Người ta dùng các viên gạch men hình vuông cạnh 4dm để lát nền căn phòng đó. Hỏi:

a) Hỏi cần bao nhiêu viên gạch men để lát kín nền căn phòng đó? (Phần diện tích mạch vữa không đáng kể).

b) Biết giá tiền 1m² gạch men loại đó là 120 000 đồng. Hỏi phải tốn bao nhiêu tiền mua gạch men để lát kín nền căn phòng đó?

Cho 2 đường thẳng xx' và yy' song song với nhau, một đường thẳng cắt xx' và yy' lần lượt tại các điểm A, A'. Kẻ tia phân giác Az của \[\widehat {x'AA'}\] và tia phân giác A't của \[\widehat {yA'A}\]. Tia Az cắt yy' tại điểm B' và A't cắt xx' tại điểm B.

a) Chứng tỏ Az // A't.

b) Chứng tỏ \[\widehat {ABA'} = \widehat {AB'A'}\].

Cho 2 đường thẳng xx' và yy' song song với nhau. Đường thẳng a cắt xx', yy' lần lượt tại A và B. Tia At là tia phân giác của \[\widehat {xAB}\].

a) Chứng minh tia At cắt đường thẳng yy'.

b) Cho \[\widehat {xAB} = 70^\circ \], At cắt yy' tại C. Tính số đo góc ACB.

Một tổ 12 người làm 4 ngày được 144 sản phẩm. Hỏi nếu muốn làm được 210 sản phẩm trong 5 ngày thì cần có bao nhiêu người?

Một tổ 15 người dự định làm xong một công việc trong 20 ngày, mỗi ngày làm 8 giờ. Hỏi tổ có thêm 5 người cùng làm, mỗi ngày làm 10 giờ thì mọi người phải làm xong việc đó trong bao nhiêu ngày?