5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 42)

Cho tứ giác MNPQ gọi R, S, T, V theo tứ tự là trung điểm của MN, NP, PQ, QM.
a) Chứng minh rằng RSTV là hình bình hành.

b) Nếu MP vuông góc với NQ thì RQTV là hình gì?

Chứng minh \({\left( {\sqrt 3 - 1} \right)^2} = 4 - 2\sqrt 3 \).

Tìm tất cả các nghiệm của phương trình cos3x+sin2x–sin4x=0.

Giải phương trình lượng giác \[{\rm{co}}{{\rm{s}}^2}x + {\rm{co}}{{\rm{s}}^2}2x + {\rm{co}}{{\rm{s}}^2}3x + {\rm{co}}{{\rm{s}}^2}4x = \frac{3}{2}\].

Giải tam giác ABC, biết \(\widehat B = 65^\circ ,\widehat C = 40^\circ \) và BC = 4,2 cm.

Cho (d₁): y = – x + 1, (d₂): y = x + 1, (d₃): y = – 1. Gọi A, B, C lần lượt là giao điểm của (d₁) và (d₂); (d₂) và (d₃), (d₁) và (d₃). Tìm tọa độ các điểm A, B, C.

Giải phương trình sin²x – cosx + 1 = 0.

Tính giá trị biểu thức P = sin² 10° +  sin² 20° + sin² 30° + … + sin² 80° là

Tìm nghiệm của phương trình: sin²x = 1.

Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm.

a) Tính số đo góc B, góc C (làm tròn đến độ) và đường cao AH.

b) Chứng minh rằng AB. cos B + AC . cosC = BC.

c) Trên cạnh AC lấy điểm D sao cho DC = 2DA. Vẽ DE vuông góc với BC tại E. Chứng minh rằng \(\frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{4}{{9D{E^2}}}\).

Tam giác ABC có AB = 3; AC = 6 và góc A = 60°. Tính bán kính của đường tròn ngoại tiếp tam giác ABC.

Cho tam giác ABC có đường trung tuyến AM bằng cạnh AC. Tính \(\frac{{\tan B}}{{\tan C}}\).

Trong một trang trại, số gà chiếm \(\frac{3}{5}\) tổng số con, số vịt chiếm \(\frac{1}{6}\) tổng số con, còn lại là ngỗng. Nhận xét nào sau đây là đúng?

Tìm một số biết rằng nếu viết thêm chữ số 6 vào bên phải số đó thì số mới hơn số cần tìm 537 đơn vị.

Cho phương trình x² – 3(m – 1)x + 2m – 4 = 0. Tìm m để phương trình có một nghiệm x = 2 và tìm nghiệm còn lại.

Phân tích đa thức thành nhân tử

a) x² – 25 + y² + 2xy;

b) x² – 2x – 4y² – 4y;

c) 16x³ + 0,25y³z³;

d) x³ – x² – x + 1;

e) x⁴ + x³ + x² – 1;

f) x⁴ + 6x²y + 9y² – 1;

g) x² + 4x – y² + 4;

h) x³ + 3x² – 3x – 1.

Cho \(\left( {{\rm{x}} + \sqrt {{x^2} + 1} } \right)\left( {y + \sqrt {{y^2} + 1} } \right) = 1\). Tính x + y.

Tính giá trị của A = (x – 3)² – (x + 1)³ + 12x(x – 1) với \(x = \frac{{ - 1}}{2}\).

Với a³ + b³ + c³ = 3abc. Tính \(P = \left( {1 + \frac{a}{b}} \right)\left( {1 + \frac{b}{c}} \right)\left( {1 + \frac{c}{a}} \right)\).

Cho tam giác ABC là tam giác đều cạnh a, M là điểm di động trên đường thẳng AC. Tìm giá trị nhỏ nhất của biểu thức \(T = \left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| + 3\left| {\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} } \right|\).

Cho x, y là hai số thực dương và \[x + y = \frac{5}{4}\]. Tìm giá trị nhỏ nhất của \(P = \frac{4}{x} + \frac{1}{{4y}}.\)

Chọn ngẫu nhiên 3 số từ tập S = {1; 2; ... ; 11}. Tính xác suất để tổng ba số được chọn là 12.

Cho tam giác ABC đều cạnh a, tâm O. Hãy tính:

a) \(\overrightarrow {AB} .\overrightarrow {AC} \).

b) \(\overrightarrow {AB} .\overrightarrow {BC} \).

c) \(\left( {\overrightarrow {OB} + \overrightarrow {OC} } \right)\left( {\overrightarrow {AB} - \overrightarrow {AC} } \right)\).

d) \(\left( {\overrightarrow {AB} + 2\overrightarrow {AC} } \right)\left( {\overrightarrow {AB} - 3\overrightarrow {BC} } \right)\).

Cho tam giác ABC đều cạnh bằng a, trọng tâm G. Tích vô hướng của hai vectơ \(\overrightarrow {BC} .\overrightarrow {CG} \) là

Có tất cả bao nhiêu số tự nhiên có 5 chữ số khác nhau mà trong đó mỗi số luôn có mặt 2 chữ số lẻ và 3 chữ số chẵn?

Cho hàm số y = ax – 4 . Tìm hệ số a, biết rằng

a) Đồ thị hàm số cắt đường thẳng y = 2x – 1 tại điểm có hoành độ bằng 2;

b) Đồ thị hàm số cắt đường thẳng y = –3x + 2 tại điểm có tung độ bằng 5.

Số giá trị nguyên của tham số m để phương trình \(\sqrt {{x^2} - m{\rm{x}} + 3} = \sqrt {2{\rm{x}} - 1} \) có hai nghiệm phân biệt là

Cho tứ giác ABCD, E là điểm thỏa mãn \(\overrightarrow {A{\rm{E}}} = \overrightarrow {EB} + 3\overrightarrow {EC} \). Vậy \(\overrightarrow {DE} = ?\)

Qua đỉnh C của hình bình hành ABCD kẻ đường thẳng song song với BD,
cắt AB ở E, cắt AD ở F.

a) Tứ giác BECD là hình gì? Vì sao?

b) Chứng minh rằng ba đường thẳng AC, BF, DE đồng quy.

Cho hình vẽ bên. Biết \(\widehat {BAC} = 123^\circ ,\widehat {ABC} = 57^\circ \), d ⊥ a = {D}. Chứng minh b ⊥ d.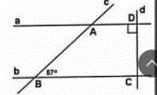

Giải phương trình: \[{\rm{cos2x}} + 2\sqrt 3 {\mathop{\rm s}\nolimits} {\rm{inx }}.{\rm{ cosx = 2}}\].

Cho a, b, c thỏa mãn \(\left\{ \begin{array}{l}a + b + c = 0\\{a^2} + {b^2} + {c^2} = 2009\end{array} \right.\).Tính A = a⁴ + b⁴ + c⁴.

Cho tam giác ABC đều cạnh a, đường cao AH. Tính độ dài của các vecto:

\(\left| {\overrightarrow {AB} + \overrightarrow {BH} } \right|,\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|,\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\).

Thế nào là hai điểm đối xứng với nhau qua một đường thẳng? Trục đối xứng của hình thang cân là đường thẳng nào?

Chứng minh

a) \(1 + {\tan ^2}\alpha = \frac{1}{{{\rm{co}}{{\rm{s}}^2}\alpha }}\).

b) \(1 + {\cot ^2}\alpha = \frac{1}{{{\rm{si}}{{\rm{n}}^2}\alpha }}\).

Đổi đơn vị thời gian:

a) \(\frac{9}{5}\) giờ = ... giờ ... phút.

b) 1,25 giờ = ... giờ ... phút.

Tìm số tự nhiên n, để

a) n + 4 ⋮ n.

b) 5n – 6 ⋮ n (n < 1).

c) 143 – 12n ⋮ n (với n < 12).

Cho các số từ 1 đến 9. Em hãy điền các số này vào các ô vuông, sao cho tổng của 3 ô hàng dọc, hàng ngang và đường chéo đều bằng nhau

Chứng minh rằng nếu một tam giác vuông có một góc nhọn bằng 30° thì cạnh góc vuông đối diện với nó bằng nửa cạnh huyền.

Tìm x biết

a) \(\sqrt {{{\left( {x - 3} \right)}^2}} = 9\).

b) \(\sqrt {4{{\rm{x}}^2} + 4{\rm{x}} + 1} = 6\).

Cho a là một số tự nhiên chia cho 19 dư 3, b là một số tự nhiên chia cho 38 dư 5. Hỏi 3a + 2b có chia hết cho 19 không?

Cho đoạn thẳng AB có trung điểm O. Vẽ về một phía của AB các tía Ax, By vuông góc với AB. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho \(\widehat {CO{\rm{D}}} = 90^\circ .\) Chứng minh AB² = 4AC . BD

Cho tam giác ABC nhọn có\(\widehat A = 70^\circ \) và điểm D thuộc cạnh BC. Gọi E là điểm đối xứng với D qua AB. Gọi F là điểm đối xứng với D qua AC. Đường thẳng EF cách AB, AC theo thứ tự tại M, N.

a) Tính các góc của tam giác AEF.

b) Chứng minh rằng DA là tia phân giác của góc MDN.

c) Tìm vị trí của D trên cạnh BC để tam giác DMN có chu vi nhỏ nhất.

Cho tam giác abc vuông tại A, M là trung điểm của BC, D, E lần lượt là hình chiếu của M trên AB và AC.

a) Tứ giác ADME là hình gì, tại sao?

b) Chứng minh \(DE = \frac{1}{2}BC\)

c) Gọi P là trung điểm của BM, Q là trung điểm của MC, chứng minh tứ giác DPQE là hình bình hành.

Từ đó chứng minh: tâm đối xứng của hình bình hành DPQE nằm trên đoạn AM.

d) Tam giác vuông ABC ban đầu cần thêm điều kiện gì để hình bình hành DPQE là hình chữ nhật?

Cho tam giác ABC điểm M nằm trong tam giác. Gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB. Gọi A’, B’, C’ thứ tự là điểm đối xứng của M qua D, E, F

a) Chứng minh tứ giác AB’A’B là hình bình hành.

b) Gọi O là giao điểm của AA’ và BB’, chứng minh C và C’ đối xứng nhau qua điểm O.

Cho điểm A nằm ngoài đường tròn (O; R). Từ A vẽ các tiếp tuyến AB, AC và cát tuyến ADE đến đường tròn (O). Gọi H là trung điểm của DE.

a) Chứng minh 5 điểm A, B, H, O, C cùng nằm trên một đường tròn.

b) Chứng minh HA là tia phân giác của góc BHC.

Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax, By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax, By lần lượt ở C và D Các đường thẳng AD và BC cắt nhau tại N.Chứng minh AB là tiếp tuyến của đường tròn đường kính CD.