5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 41)

May 13 chiếc áo hết 19,5 m vải, may 12 cái quần hết 12,6 m. Hỏi may bộ quần áo hết bao nhiêu m vải?

Một ô tô cứ đi 100 km thì tiêu thụ hết 12,5 lít xăng.Hỏi ô tô đó đi quãng đường dài 60 km thì tiêu thụ hết bao nhiêu xăng?

Thương của hai số bằng 468. Nếu giữ nguyên số bị chia và số chia gấp lên 18 lần thì được thương mới là bao nhiêu ?

Tổng của tất cả các số nguyên a mà –7 < a ≤ 7 bằng bao nhiêu?

Trong 4 giờ xe máy đi được 121 km, trong 2 giờ ô tô đi được 111km. Hỏi trung bình mỗi giờ ô tô đi được nhiều hơn xe máy bao nhiêu km?

Tìm các chữ số a, b, c, d sao cho tổng abc + dba chia hết cho aa và được thương là aa (abc, dba là các số có 3 chữ số theo thứ tự là a, b, c và d, b, a; aa là số có 2 chữ số đều bằng a).

Tìm hai số biết tổng của hai số đó là 102,1. Nếu số thứ nhất gấp 5 lần và giữ nguyên số thứ hai thì tổng mới bằng 329,3.

Tìm x, biết: 35,8 + x × 4 = 100.

Cho hàm số \(y = {x^4} + m{x^3} - 2{x^2} - 3mx + 1\left( 1 \right)\). Xác định m để (1) có 2 cực tiểu.

Hàm số \(y = 5{x^2} - 6x + 7\) có giá trị nhỏ nhất khi nào?

Tìm x: (x – 12) – 15 = 20 – (17 + x).

Tìm x thuộc Ư(20)và x > 8.

Tìm x, biết: 5.(12 – x) – 20 = 30.

Chứng minh đẳng thức: \(\left( {a + b} \right)\left( {c + d} \right) - \left( {a + d} \right)\left( {b + c} \right) = \left( {a - c} \right)\left( {d - b} \right)\).

Một hồ bơi dạng hình hộp chữ nhật có kích thước trong lòng hồ là: Chiều dài 12m, chiều rộng 5m, chiều sâu 3m.

a. Tính thể tích của hồ bơi.

b. Tính diện tích cần lát gạch bên trong lòng hồ (mặt đáy và 4 mặt xung quanh).

c. Biết gạch hình vuông dùng để lát hồ bơi có cạnh 50cm. Hỏi cần mua ít nhất bao nhiêu viên gạch để lát bên trong hồ bơi.

Tìm x biết: \(x\left( {\frac{1}{{10.11}} + \frac{1}{{11.12}} + \frac{1}{{12.13}} + \frac{1}{{13.14}} + \frac{1}{{14.15}}} \right) = 67,3\).

Trong phép tính 121,23 : 14 và có thương là 8,65, vậy số dư là bao nhiêu?

Giá trị biểu thức 15,5 + 6,25 : 25 là

Tính nhanh: 0,8 × 96 + 1,6 × 2.

Tính nhanh: 3,6 : 0,5 + 1,8 × 8 + 3,6 : 0,25.

Tìm x biết: 2x–(–17)=15.

Số dư của phép chia 37,99:16 nếu lấy đến 2 chữ số ở phần thập phân của thương là bao nhiêu?

Cho a và b là hai số tự nhiên. Biết a chia cho 3 dư 1; b chia cho 3 dư 2. Chứng minh rằng ab chia cho 3 dư 2.

Tính: (131,4 – 80,8) : 2,3 + 21,84 × 2.

Hai số thập phân có tổng là 55,22. Nếu dời dấu phẩy của số bé sang trái một hàng, rồi lấy hiệu giữa số lớn và số bé ta được 37,07. Tìm 2 số đó?

Hai số thập phân có hiệu là 5,37. Nếu dời dấu phẩy của số lớn sang trái 1 hàng rồi cộng với số bé ta được 11,955. Tìm 2 số đó?

Tìm một số có hai chữ số biết nếu viết số 0 vào giữa hai chữ số của số đó ta được số mới gấp 7 lần số phải tìm?

Một can nước (tính cả vỏ can) nặng 12 kg. Sau đó người ta đổ bớt \(\frac{1}{3}\) số nước ra ngoài. Biết rằng can rỗng nặng 600 g. Hỏi sau khi đổ bớt nước ra ngoài, can nước cân nặng bao nhiêu?

Một hình chữ nhật có chiều dài 25,4 m, chiều rộng bằng 4,6 m. Tính chu vi và diện tích hình chữ nhật đó.

Một hình chữ nhật có chiều dài \(\frac{4}{5}\) m và chiều rộng bằng \(\frac{3}{4}\) chiều dài. Tính chu vi và diện tích hình chữ nhật đó.

Mua 12 quyển vở hết 24 000 đồng. Mua 30 quyển vở như thế hết bao nhiêu tiền?

Các cột điện trước đây cách nhau 60m, hiện nay trồng lại cách nhau 45m. Hỏi sau cột đầu tiên không phải trồng lại thì cột gần nhất không phải trồng lại là cột thứ mấy?

Tổng của hai số là 0,6. Thương của hai số cũng bằng 0,6. Tìm hai số đó?

Tìm x ∈ ℚ để biểu thức \(\left| {x + 5} \right| + \left| {x - 7} \right|\) đạt giá trị nhỏ nhất.

Cho tứ giác ABCD có góc \(\widehat B = \widehat D = 90^\circ \).

a. Chứng minh rằng 4 điểm A, B, C, D cùng thuộc một đường tròn, tìm tâm đường tròn đó.

b. So sánh độ dài AC và BD. Tứ giác ABCD cần thêm điều kiện gì thì AC = BD?

Cho 2 tập hợp \(M = \left[ {2m - 1;2m + 5} \right]\) và \(N = \left[ {m + 1;m + 7} \right]\)(với m là tham số thực). Tính tổng tất cả các giá trị của m để hợp của 2 tập hợp M và N là 1 đoạn có độ dài bằng 10.

Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{mx + y = 3m - 1}\\{x + my = m + 1}\end{array}} \right.\). Tìm m để hệ:

a. Có nghiệm duy nhất.

b. Có vô số nghiệm.

c. Vô nghiệm

Xác định các tập hợp sau và biểu diễn chúng trên trục số:

a. [– 3; 7] ∩ (2; 5).

b. (– ∞; 0] ∪ (–1; 2).

c. ℝ \ (– ∞; 3).

Xác định các tập hợp sau và biểu diễn chúng trên trục số.

a. (−∞;1)∩(0;+∞).

b. (4;7]∪(−1;5).

c. (4;7]\(−3;5].

Tìm ba chữ số tận cùng của tích mười hai số nguyên dương đầu tiên.

Cho x,y × 9,9 = xx,yy. Hãy tìm chữ số thích hợp thay cho x và y để được phép tính đúng với x và y khác nhau và khác 0 .

Tìm nghiệm nguyên của phương trình x² + 5y² + 6z² + 2xy – 4xz = 10.

Cho 3 số dương x, y, z thỏa mãn điều kiện: xy + yz +zx = 1. Tính:

\(A = x\sqrt {\frac{{\left( {{y^2} + 1} \right)\left( {{z^2} + 1} \right)}}{{{x^2} + 1}}} + y\sqrt {\frac{{\left( {1 + {z^2}} \right)\left( {1 + {x^2}} \right)}}{{1 + {y^2}}}} + z\sqrt {\frac{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)}}{{1 + {z^2}}}} \).

Tính bằng cách thuận tiện nhất: 0,125 × 6,94 × 80.

Tìm x thuộc ℤ biết: 11 ⁝ (2x + 1).

Hai đội công nhân cùng làm một đoạn đường trong 24 ngày thì xong. Mỗi ngày đội thứ hai làm được khối lượng công việc nhiều gấp đôi đội thứ nhất. Hỏi nếu làm một mình thì mỗi đội làm xong đoạn đường đó trong bao lâu?

Tính nhanh: 245,9 × 0,49 – 245,9×0,58 + 24,59 × 10.

Tính bằng cách thuận tiện nhất: 28 + 62 × a × (a × 1 – a: 1 ) + 28 × 8 + 28.

Thực hiện phép tính: \(\frac{3}{4}.\frac{8}{9}.\frac{{15}}{{16}}.....\frac{{80}}{{81}}.\frac{{99}}{{100}}\).

Chứng minh rằng: \(\overline {ababab} \vdots 3\).

Cho 2 đường tròn (O) và (O') tiếp xúc ngoài ở A. Một cát tuyến kẻ qua A cắt (O) ở B; cắt (O') ở C. Kẻ đường kính BD và CE của (O) và (O'). Chứng minh:

a. D, A, E thẳng hàng.

b. BD song song CE.

Cho 4 số nguyên dương a, b, c, d trong đó b là trung bình cộng của a và c đồng thời \(\frac{1}{c} = \frac{1}{2}\left( {\frac{1}{b} + \frac{1}{d}} \right)\). Chứng minh: \(\frac{a}{b} = \frac{c}{d}\).

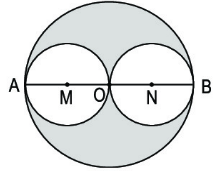
Cho hình tròn tâm O, đường kính AB = 8 cm.

a. Tính chu vi hình tròn tâm O đường kính AB, hình tròn tâm M, đường kính AO và hình tròn tâm N, đường kính OB.

b. So sánh tổng chu vi của hình tròn tâm M và hình tròn tâm N với chu vi hình tròn tâm O.

c. Tính diện tích phần đã tô đậm của hình tròn tâm O.

Cho đường tròn tâm O có bán kính OA = 8cm, dây BC của đường tròn vuông góc với OA tại trung điểm I của OA. Tính BC.

Cho nửa đường tròn tâm O đường kính AB. Ax là tia tiếp tuyến của nửa đường tròn (Ax và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB), từ điểm C trên nửa đường tròn (C ≠ A, B) vẽ tiếp tuyến CM cắt Ax tại M, hạ CH vuông góc với AB tại H, MB cắt (O) tại Q và cắt CH tại N.

a) Chứng minh MA² = MQ.MB.

b) MO cắt AC tại I. Chứng minh tứ giác AIQM nội tiếp.

c) Chứng minh: IN ⊥ CH.

Cho ∆ABC có AB=AC.Tia phân giác góc A cắt BC tại D.

a. Chứng minh ∆ADB= ∆ADC.

b. Chứng minh AD ⊥ BC.

c. Kẻ DH ⊥ AB (H ∈ AB), DK ⊥ AC (K ∈ AC). Chứng minh DH=DK.

Cho ∆ABC vuông tại A, đường cao AH. Gọi HD, HE lần lượt là đường cao của ∆AHB và ∆AHC. Chứng minh rằng:

a) \(\frac{{A{B^2}}}{{A{C^2}}} = \frac{{HB}}{{HC}}\).

b) \(\frac{{A{B^3}}}{{A{C^3}}} = \frac{{BD}}{{EC}}\).