5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 40)

Cho tam giác ABC nhọn (AB < AC), đường cao AH. Gọi M, N lần lượt là hình chiếu của H trên AB, AC. Tính AH, MH biết AM = 8 cm; BM = 2 cm.

Tìm tất cả giá trị thực của tham số m để tập hợp (1;m) chứa đúng hai số nguyên dương.

Cho hàm số y = 2x + 3.

a) Vẽ đồ thị hàm số trên.

b) Gọi A, B là giao điểm của đồ thị với các trục tọa độ. Tính diện tích tam giác OAB (O là gốc tọa độ và đơn vị trên các trục tọa độ là cm).

c) Tính góc tạo bởi đường thẳng y = ax + b và trục Ox.

Xét sự đơn điệu của hàm số \(y = - \frac{1}{x}\).

Cho \(\cos a = - \frac{2}{5}\). Tính các giá trị lượng giác còn lại của góc a biết a ∈ (0; 2π).

Cho nửa đường tròn tâm O có đường kính AB = 2R. Kẻ hai tiếp tuyến Ax, By của nửa đường tròn (O) tại A và B (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D.

a) Chứng minh tam giác COD vuông tại O.

b) Chứng minh AC.BD=R².

c) Kẻ MH vuông góc AB (H ∈ AB). Chứng minh rằng BC đi qua trung điểm của đoạn MH.

Cho tam giác ABC có\(\widehat {BAC} = 60^\circ \), phân giác AD. Chứng minh hệ thức\(\frac{{\sqrt 3 }}{{A{\rm{D}}}} = \frac{1}{{AB}} + \frac{1}{{AC}}\).

Cho tam giác ABC có \(\widehat {ABC} = 30^\circ \), AB=5, BC=8. Tính \(\overrightarrow {BA} .\overrightarrow {BC} \).

Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn (O), nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và E.

a) Chứng minh rằng chu vi tam giác ADE bằng 2AB.

b) \(\widehat {DOE} = \frac{1}{2}\widehat {BOC}\).

Có 4 bao tải gạo, bao thứ hai nặng gấp đôi bao thứ nhất, bao thứ ba nặng hơn bao thứ hai 12,5 kg, bao thứ tư ít hơn bao thứ ba 6,3kg. Biết rằng cả 4 bao có tất cả 53,7kg gạo. Hỏi bao thứ ba có bao nhiêu kg gạo?

Nghiệm của phương trình sin2x+cosx=0 là

Cho biểu thức: \(A = \frac{{x - 3}}{x} - \frac{x}{{x - 3}} + \frac{9}{{{x^2} - 3{\rm{x}}}}\).

a) Rút gọn biểu thức A.

b) Tìm giá trị của x để A =– 3.

Chứng minh rằng với mọi giá trị của m:

a) Phương trình: mx² – (3m + 2)x + 1 = 0 luôn có nghiệm.

b) Phương trình: \(({m^2} + 5){x^2} - \left( {\sqrt 3 m - 2} \right)x + 1 = 0\) luôn vô nghiệm.

Cho hình vẽ dưới đây. Hãy chứng tỏ CD // EF.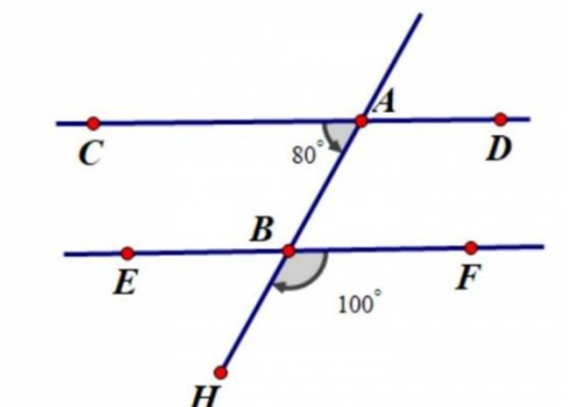

Tom và Jerry chơi trò chơi bốc kẹo. Ban đầu trên bàn có 24 chiếc kẹo. Bắt đầu từ Tom, hai bạn luân phiên nhau bốc kẹo, mỗi lần được bốc từ 1 đến 5 chiếc kẹo. Ai lấy được chiếc kẹo cuối cùng là người thắng cuộc. Biết cả hai đều chơi thông minh, hỏi ai là người thắng cuộc?

Giải phương trình sau:\(\frac{{{\rm{cos4x}} - 6{{\sin }^2}x + 2}}{{2{\mathop{\rm s}\nolimits} {\rm{inx}} - 1}} = 0\).

Giải phương trình sau:\({\sin ^4}x + c{\rm{o}}{{\rm{s}}^4}\left( {x + \frac{\pi }{4}} \right) = \frac{1}{4}\).

Cho biểu thức \(A = \left( {\frac{{\sqrt x + 2}}{{\sqrt x - 2}} - \frac{{\sqrt x - 2}}{{\sqrt x + 2}} + \frac{{4{\rm{x}}}}{{x - 4}}} \right):\frac{{4\left( {\sqrt x + 2} \right)}}{{\sqrt x - 2}}\) với x ≥ 0, x ≠ 4.

a) Rút gọn biểu thức A.

b) So sánh A và \(\sqrt A \).

Trong mặt phẳng Oxy, cho đường thẳng d: 2x – y = 0. Phương trình đường thẳng qua phép đồng dạn có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = – 2 và phép đối xừng trục Oy là đường thẳng nào sau đây?

Tính A = (x – 2)(x⁴ + 2x³ + 4x² + 8x + 16) tại x = 3.

Cho các tập hợp A = (–2; 10), B = (m; m + 2). Tìm m để tập hơp A ∩ B là một khoảng:

Cho đường tròn tâm O có bán kính OA = R, dây BC vuông góc với OA tại trung điểm M của OA.

a) Tứ giác OCAB là hình gì? Vì sao?

b) Kẻ tiếp tuyến với đường tròn tại B, nó cắt đường thẳng OA tại E. Tính độ dài BE theo R.

Cho hình lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Tính thể tích khối tứ diện A’BB’C’.

Cho nửa đường tròn (O; R) đường kính AB. Trên đoạn OB lấy điểm H sao cho HB = 2HO. Đường thẳng vuông góc với AB tại H cắt nửa (O) tại D. Vẽ đường tròn (S) đường kính AO cắt AD tại C.

a) Chứng minh C là trung điểm của AD.

b) Chứng minh 4 điểm C, D, H, O cùng thuộc một đường tròn.

c) CB cắt DO tại E. Chứng minh BC là tiếp tuyến của (S).

d) Tính diện tích tam giác AEB theo R.

Cho tam giác ABC có M, N lần lượt là trung điểm của AC, AB. Gọi E là điểm đối xứng với B qua M; F là điểm đối xứng với C qua N.

a) Chứng minh tứ giác ABCE là hình bình hành.

b) Chứng minh E đối xứng với F qua A.

Cho tam giác ABC có ba góc nhọn (AB<AC) nội tiếp đường tròn (O; R). Vẽ  AH vuông góc với BC. Từ H vẽ HM vuông góc với AB và HN vuông góc với AC (H ∈ BC, M ∈ AB, N ∈ AC). Vẽ đường kính AE cắt MN tại I, tia MN cắt đường tròn (O;R) tại K

a) Chứng minh tứ giác AMHN nội tiếp.

b) Chứng minh AE vuông góc với MN.

c) Chứng minh AH = AK.

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc (ABCD) và SA =2a.

a) Chứng minh (SCD) vuông góc (SAD).

b) Tính d(A,(SCD)).

Chứng minh đẳng thức: \(\frac{{1 + {\mathop{\rm s}\nolimits} {\rm{inx}}}}{{1 - {\mathop{\rm s}\nolimits} {\rm{inx}}}} + \frac{{1 - {\mathop{\rm s}\nolimits} {\rm{inx}}}}{{1 + {\mathop{\rm s}\nolimits} {\rm{inx}}}} = 2\left( {1 + 2{{\tan }^2}x} \right)\).

Tìm x biết: sin²x + sin² 2x + sin² 3x = 2.

Cho biểu thức \[{\rm{A}} = \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{{\sqrt x }}{{\sqrt x - 3}}\] và \(B = \frac{{\sqrt x - 3}}{{\sqrt x - 1}}\) với x ≥ 0, x ≠1, x ≠ 9.

a) Tính giá trị của B khi x = 25.

b) Rút gọn biểu thức M = A.B.

c) Tìm x sao cho \(M < \sqrt M \).

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của SA, SB, SC. Tìm giao điểm Q của SD và (MNP).

Cho biểu thức \(P = \left( {1 - \frac{{\sqrt x }}{{\sqrt x + 1}}} \right):\left( {\frac{{\sqrt x + 2}}{{\sqrt x + 3}} + \frac{{\sqrt x - 3}}{{2 - \sqrt x }} + \frac{{\sqrt x - 2}}{{x + \sqrt x - 6}}} \right)\).

a) Rút gọn P.

b) Tính giá trị của P biết \(x = \frac{{3 - \sqrt 5 }}{2}\).

c) Tìm các giá trị x nguyên để P nhận giá trị nguyên.

d) Tìm x để P < 1.

e) Tìm các giá trị của x để \(P = \sqrt x - 3\).

Cho x × 16 + 4236 = 8860. Khi đó x là bao nhiêu?

Tính nhanh giá trị của đa thức:

a) \[{{\rm{x}}^2} + \frac{1}{2}x + \frac{1}{{16}}\] tại x = 49,75.

b) x² – y² – 2y – 1 tại x = 93 và y = 6.

Tính giá trị biểu thức \(P = \frac{{2\sin {\rm{a}} + 3co{\rm{sa}}}}{{4\sin {\rm{a}} - 5co{\rm{sa}}}}\) biết tana = 3.

Cho ΔABC vuông tại A, \(BC = 3\sqrt 5 \) cm. Hình vuông ADEF có cạnh 2 cm, D ∈ AB, E ∈ BC, F ∈ AC.

a) Tính AB, AC.

b) Tính diện tích, chu vi ΔABC.

Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, AD = 2a; cạnh bên SA = a và vuông góc với đáy. Tính khoảng cách d từ A tới mặt phẳng (SBD).

Giải phương trình \(2{\sin ^2}x + \sqrt 3 \sin 2{\rm{x}} = 3\) được nghiệm là

Tìm x nguyên thỏa mãn \(\frac{{x + 5}}{{x + 2}}\) là số nguyên.

Trên bàn có một số cái bánh, Dương ăn \(\frac{5}{8}\) cái bánh, My ăn \(\frac{7}{{12}}\) cái bánh, Lan ăn \(\frac{9}{5}\) cái bánh. Hỏi trên bàn có ít nhất bao nhiêu cái bánh?

Giải phương trình: \(\frac{1}{{\sin 2{\rm{x}}}} + \frac{1}{{cos2{\rm{x}}}} = \frac{2}{{\sin 4{\rm{x}}}}\).

Cho đường tròn (O; 2cm) và một điểm A chạy trên đường tròn đó. Từ A vẽ tiếp tuyến xy. Trên tia Ax lấy điểm M sao cho \[{\rm{A}}M = 2\sqrt 3 \]cm. Hỏi điểm M di động trên đường nào khi A chạy trên (O).

Cho hai tập hợp A = [m + 1; m + 4] và B = ( – ∞; 5). Tìm tất cả các giá trị của m để A ∩ B = ∅

Cho hình bình hành ABCD tâm O. Gọi M là 1 điểm bất kỳ. Chứng minh

a) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {M{\rm{D}}} = 4\overrightarrow {MO} \)

b) \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {A{\rm{D}}} = 2\overrightarrow {AC} \).