5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 37)

Phân tích đa thức thành nhân tử:

a) x² – xy + 2x – 2y.

b) x² + 10xy – 25 + 25y².

Cho biểu thức $P=\left(\frac{1}{x-\sqrt{x}}+\frac{1}{\sqrt{x}-1}\right):\frac{\sqrt{x}}{x-2\sqrt{x}+1}$.

a) Rút gọn biểu thức P.

b) Tìm các giá trị của x để $P>\frac{1}{2}$.

Cho biểu thức $P=\frac{15\sqrt{x}-11}{x+2\sqrt{x}-3}+\frac{3\sqrt{x}-2}{1-\sqrt{x}}-\frac{2\sqrt{x}+3}{\sqrt{x}+3}$

a) Rút gọn biểu thức P.

b) Tìm giá trị của x sao cho $P<\frac{1}{2}$.

c) Tìm các giá trị nguyên của x sao cho giá trị tương ứng của biểu thức P nguyên.

Tìm số tự nhiên có 3 chữ số biết rằng nếu xóa chữ số 2 ở hàng trăm của số đó thì được số mới bằng $\frac{1}{9}$ số đó.

Tìm số nguyên x, y biết xy – 2x – 3y = 1.

Cho tam giác ABC vuông tại A, đường cao AH. Biết $\frac{AC}{AB}=\sqrt{2}$, HC – HB = 2. Tính:

a) Tỉ số $\frac{HC}{HB}$.

b) AB, BC, CA.

Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số: y = 4sin²x – 4sinx + 3.

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: y = 4sin²x – 4sinx + 1.

Tập nghiệm S của phương trình cos²x – 3cosx = 0 là

Giải phương trình: cos²x + 3cosx = 0.

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, chiều cao bằng $a\sqrt{2}$. Tính khoảng cách từ tâm O của đáy ABCD đến một mặt bên.

Cho hình chóp tứ giác đều S.ABCD, đáy có tâm O và cạnh bằng a, cạnh bên bằng a. Khoảng cách từ O đến (SAD) bằng bao nhiêu?

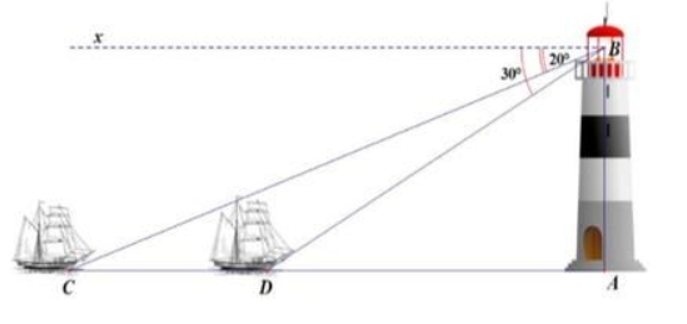
Một người đứng trên tháp quan sát của ngọn hải đăng cao 50 m nhìn về hướng Tây Nam, người đó quan sát hai lần một con thuyền đang hướng về ngọn hải đăng. Lần thứ nhất người đó nhìn thấy thuyền với góc hạ là 20°, lần thứ 2 người đó nhìn thấy thuyền với góc hạ là 30°. Hỏi con thuyền đã đi được bao nhiêu mét giữa hai lần quan sát? (làm tròn đến chữ số thập phân thứ nhất)

Cho biểu thức $P=\frac{\sqrt{x}-2}{\sqrt{x}+1}$. Tìm x để $\sqrt{P}<\frac{1}{2}$.

Tính tổng của các số nguyên x thỏa mãn $-2009<x\le 2008$.

Chứng minh các hệ thức:

a) $1+{\tan }^{2}a=\frac{1}{{\cos }^{2}a}$;

b) $1+{\cot }^{2}a=\frac{1}{{\sin }^{2}a}$.

Cho x, y > 0 thỏa mãn x + y ≥ 6. Tìm giá trị nhỏ nhất của $P=5x+3y+\frac{10}{x}+\frac{8}{y}$.

Cho đường tròn (O) dây cung BC (BC không là đường kính). Điểm A di động trên cung nhỏ BC (A khác B và C, độ dài cạnh AB khác AC). Kẻ đường kính AA' của đường tròn (O), D là chân đường vuông góc kẻ từ A đến BC. Hai điểm E, F lần lượt là chân đường vuông góc kẻ từ B, C đến AA'.

a) Chứng minh rằng 4 điểm A, B, D, E cùng nằm trên 1 đường tròn.

b) Chứng minh BD.AC = AD.A'C.

sin15° bằng bao nhiêu?

Cho $\sin 15°=\frac{\sqrt{6}-\sqrt{2}}{4}$.

a) Tính sin75°, cos105°, tan165°.

b) Tính giá trị của biểu thức: A = sin75°. cos165° + cos105°. sin165°.

Trong khai triển nhị thức (3 + 0,02)⁷. Tìm tổng của ba số hạng đầu tiên.

Cho hình thang ABCD có đáy AB, DC. Gọi M, N lần lượt là trung điểm AD và BC. Chứng minh MN // DC và $MN=\frac{1}{2}\left(AB+DC\right)$.

Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC.

a) Chứng minh hai tam giác ABM và ACM bằng nhau.

b) Chứng minh AM vuông góc với BC.

c) Chứng minh AM là phân giác của góc A.

Cho tam giác ABC vuông cân tại A có $BC=a\sqrt{2}$. Tính $\overrightarrow{CA}.\overrightarrow{CB}$.

Cho tam giác ABC vuông cân tại A, cạnh AB = a. Khi đó $\left|2\overrightarrow{AB}-\overrightarrow{AC}\right|$ bằng

Cho tứ diện đều ABCD, cạnh a. Gọi I, J lần lượt là trung điểm của AC, BC. Gọi K là một điểm trên cạnh BD với KB = 2KD.

a) Xác định thiết diện của tứ diện với mp(IJK). Chứng minh thiết diện là hình thang cân.

b) Tính diện tích thiết diện đó.

Cho tứ diện đều ABCD cạnh a. Gọi I, J lần lượt là trung điểm của AC và BC. Gọi K là điểm trên cạnh BD với KB = 2KD. Thiết diện của tứ diện với mặt phẳng (IJK) là hình gì?

Cho đường tròn (O; R) và điểm A cố định ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên d lấy M. Qua M kẻ tiếp tuyến ME, MF với (O). Nối EF cắt OM tại H, cắt OA tại B.

a) Chứng minh tứ giác ABHM nội tiếp.

b) Chứng minh OA.OB = OH.OM = R².

c) Chứng minh tâm I của đường tròn nội tiếp tam giác MEF thuộc một đường tròn cố định khi M di chuyển trên d.

d) Tìm vị trí của M để diện tích tam giác HBO lớn nhất.

Cho đường tròn (O; R) và điểm A cố định ở ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên d lấy điểm M. Qua M kẻ hai tiếp tuyến ME, MF tới đường tròn (O; R) tiếp điểm lần lượt là E và F. Nối EF cắt OM tại H, cắt OA tại B.

a) Chứng minh OM vuông góc với EF.

b) Cho biết R = 6cm, OM = 10cm. Tính OH.

c) Chứng minh 4 điểm A, B, H, M cùng thuộc một đường tròn.

d) Chứng minh tâm I của đường tròn nội tiếp tam giác MEF thuộc một đường tròn cố định khi M chuyển động trên d.

Cho (O) đường kính AB = 10cm, C là 1 điểm trên đường tròn (O) sao cho AC = 6cm. Vẽ CH vuông góc với AB (H thuộc AB).

a) Tính AH và góc ABC.

b) Tiếp tuyến tại B và C của (O) cắt nhau tại D. Chứng minh rằng OD vuông góc với BC.

c) Tiếp tuyến tại A của (O) cắt BC tại E. Chứng minh CE.CB = AH.AB.

d) Gọi I là trung điểm của CH tia BI cắt AE tại F. Chứng minh FC là tiếp tuyến của (O).

Giả sử A, B, C là ba góc của tam giác ABC, chứng minh rằng: 

$\sin A+\sin B+\sin C=4\cos \frac{A}{2}\cos \frac{B}{2}\cos \frac{C}{2}$

Cho tam giác ABC, chứng minh rằng: $\sin A+\sin B+\sin C\le \frac{3\sqrt{3}}{2}$.      

Có bao nhiêu phân số với mẫu số có 2 chữ số tương đương với $\frac{1}{5}$?

Cho đường tròn tâm O, bán kính R, điểm A cố định thuộc đường tròn. Trên tiếp tuyến với đường tròn tại A lấy K cố định. Một đường thẳng d đi qua K và không đi qua tâm O cắt đường tròn tâm O tại hai điểm B và C (B nằm giữa C và K). Gọi M trung điểm BC

a) Chứng minh 4 điểm A, O, M, K cùng thuộc 1 đường tròn.

b) Vẽ đường kính AN của đường tròn tâm O. Đường thẳng qua A và vuông góc BC cắt MN tại H. Chứng minh tứ giác BHCN là hình bình hành.

c) Chứng minh H là trực tâm của tam giác ABC.

d) Khi đường thẳng d thay đổi và thỏa mãn điều kiện đề bài thì H di động trên đường nào?

Cho đường tròn (O; R) và điểm A là một điểm cố định thuộc đường tròn. Kẻ đường thẳng d tiếp xúc với đường tròn tại A. Trên đường thẳng d lấy điểm M (M khác A), kẻ dây cung AB vuông góc với OM tại H.

a) Chứng minh BM tiếp tuyến của (O) và bốn điểm A; O; M; B cùng thuộc 1 đường tròn.
b) Kẻ đường kính AD của (O), đoạn thẳng DM cắt đường tròn (O) tại điểm thứ 2 là E. Chứng minh MA² = MH.MO = ME.MD , từ đó suy ra $\widehat{EHM}=\widehat{ODM}$.

Diện tích hình bình hành bằng 24 cm². Khoảng cách từ giao điểm hai đường chéo đến các cạnh hình bình hành bằng 2 cm và 3 cm. Tính chu vi của hình bình hành.

Cho hàm số y = (2 – m)x + 3.

a) Tìm m để (d) đi qua điểm A(2; 3).

b) Tìm m để (d) cắt trục hoành tại điểm có hoành độ là –1.

c) Tìm m để (d) cắt trục tung tại điểm có tung độ là 3.

Cho hàm số y = (a – 2)x + 5 có đồ thị là đường thẳng d. Tìm a để đường thẳng d đi qua điểm M(2; 3).

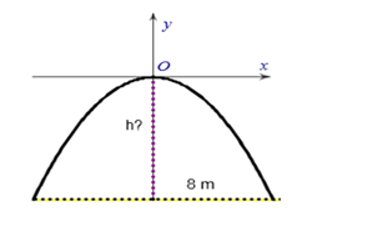
Một chiếc cổng hình parabol dạng $y=-\frac{1}{2}{x}^2$ có chiều rộng d = 8 m. Hãy tính chiều cao h của cổng (Xem hình minh họa bên cạnh).

Một lớp học có 40 học sinh trong đó có 15 học sinh giỏi Toán, 10 học sinh giỏi Văn và 5 học sinh giỏi cả Văn và Toán. Chọn ngẫu nhiên một học sinh. Xác suất của biến cố C: “Học sinh được chọn không giỏi Văn và Toán” là:

Một lớp học có 40 học sinh trong đó có 15 học sinh giỏi Toán, 10 học sinh giỏi Văn và 5 học sinh giỏi cả Văn và Toán. Chọn ngẫu nhiên một học sinh.

Xác suất của biến cố A: “Học sinh được chọn giỏi Toán” là:

Cho hình chóp S.ABCD đáy là hình bình hành. Gọi I, J lần lượt là trung điểm của SB, AB. Điểm M là một điểm bất kì trên nửa đường thẳng Ax chứa C. Biện luận theo vị trí của điểm M trên Ax các dạng của thiết diện của hình chóp cắt bởi mặt phẳng (IJM).

Cho tam giác AEB vuông tại A, từ điểm C trên cạnh BE kẻ đường vuông góc với BE cắt tia đối của tia AB ở F, cắt AE ở D. Tia phân giác của góc E cắt AB, CD lần lượt ở M, P. Tia phân giác của góc F cắt BC, DA lần lượt ở N và Q. Chứng minh:

a) EM vuông góc với FN.

b) Tứ giác MPNQ là hình thoi.

Cho (O), điểm A ở bên ngoài đường tròn. Vẽ các tiếp tuyến AB, AC và cát tuyến ADE. Gọi H là trung điểm của DE.

a) Chứng minh 5 điểm A, B, H, O, C cùng thuộc 1 đường tròn.

b) Chứng minh HA là tia phân giác của góc BHC.

c) Gọi I là giao của BC và DE. Chứng minh AB² = AI.AH.

d) BH cắt (O) ở K. Chứng minh AE // CK.

Cho đường thẳng (d): y = (m² – 3)x – m + 1. Tìm m để (d) cắt (d’): y = –2x tại điểm có hoành độ x = 2.

Mỗi giờ ô tô đi được 43,8km. Hỏi trong 5 giờ ô tô đi được số ki lô mét là bao nhiêu?

Tính giới hạn: $\lim \left[\frac{1}{1.3}+\frac{1}{3.5}+\mathrm{...}+\frac{1}{\left(2n-1\right)\left(2n+1\right)}\right]$.

Một mảnh đất hình thoi có tổng độ dài hai đường chéo là là 76,4m. Tính diện tích mảnh đất đó, biết đường chéo thứ nhất hơn đường chéo thứ 2 là 4,4m.

Rút gọn phân thức $\frac{5x^2-10xy}{2{\left(2y-x\right)}^3}$.

Rút gọn phân thức $\frac{5x^2-10xy}{2{\left(2y-x\right)}^2}$.

Trong một cuộc thi chạy, nếu bạn vượt qua người thứ 2, bạn sẽ đứng thứ mấy?

Để sửa một ngôi nhà cần một số thợ làm việc trong một thời gian quy định. Nếu giảm ba người thì thời gian kéo dài sáu ngày. Nếu tăng thêm hai người thì xong sớm hai ngày. Hỏi theo quy định cần bao nhiêu thợ và làm trong bao nhiêu ngày. Biết rằng khả năng lao động của mọi thợ đều như nhau?

Cho tam giác ABC nhọn nội tiếp đường tròn tâm O, bán kính R. Đường cao BD, CE cắt nhau tại H. Vẽ đường kính AF của đường tròn tâm O. Gọi I là trung điểm của BC.

a) Chứng minh H, I, F thẳng hàng.

b) Chứng minh AH = 2OI.

c) Gọi G là trọng tâm của tam giác ABC. Chứng minh $S_{\Delta AHG}=2S_{\Delta AGO}$.

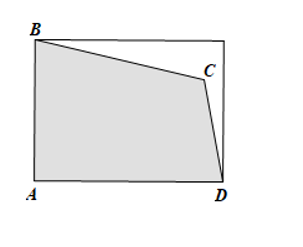
Một mảnh đất hình chữ nhật bị xén đi một góc (hình vẽ), phần còn lại có dạng hình tứ giác ABCD với độ dài các cạnh là AB = 15m, BC = 19m, CD = 10m, DA =  20m. Diện tích mảnh đất ABCD bằng bao nhiêu mét vuông (làm tròn kết quả đến hàng đơn vị).    

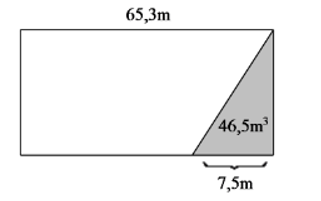
Một miếng đất hình chữ nhật có chiều dài 65,3m. Vì mở rộng đường quốc lộ nên miếng đất bị xén đi một góc có dạng hình tam giác (phần tô đậm của hình vẽ). Tính diện tích phần đất còn lại.