5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 35)

Giải phương trình: cos3x + cosx – cos2x = 0.

Giải phương trình: cos3x.cosx = cos2x.

Giải phương trình: cos3x.cosx = cos2x.

Tính \({\left( {a - b - c} \right)^3}\).

Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{{x^4} + 2{x^3}y + {x^2}{y^2} = 2x + 9}\\{{x^2} + 2xy = 6x + 6}\end{array}} \right.\).

Hình vuông có cạnh bằng 2 thì đường chéo hình vuông đó bằng bao nhiêu?

Chứng minh \(A \cup B = A \cap B\) thì A = B.

Xác định các tập hợp A\( \cup B\) và \(A \cap B\) với: A = {đỏ; cam; vàng; lục; lam}, B = {lục; lam; chàm; tím}.

Cho \(\Delta ABC\) đều cạnh a. Tính độ dài vectơ \(\overrightarrow {AB} - \overrightarrow {AC} \) và \(\overrightarrow {AB} + \overrightarrow {AC} \).

Cho phương trình: \(\cos \left( {2x - \frac{\pi }{3}} \right) - m = 2\). Tìm m để phương trình có nghiệm.

Giải phương trình sinxcosx + 2(sinx + cosx) = 2.

Hai đường thẳng xy và zt cắt nhau tại O sao cho \(\widehat {xOz} = 70^\circ \).

a. Tính số đo các góc tạo thành.

b. Vẽ tia Om là tia phân giác của \(\widehat {zOy}\) và vẽ tia On là tia đối của tia Om.

Tính số đo \(\widehat {xOn}\), từ đó chỉ ra tia Ox không là tia phân giác của \(\widehat {zOn}\).

Một cánh đồng lúa thực nghiệm hình chữ nhật có chiều dài 1200m, chiều rộng bằng \(\frac{3}{5}\) chiều dài. Người ta cấy giống lúa với năng xuất đạt 5 tấn trên 1 ha. Hỏi cả cánh đồng lúa thực nghiệm đó sẽ thu hoạch được bao nhiêu tấn thóc?

Cho biểu thức: \(A = \frac{{2\sqrt x - 9}}{{x - 5\sqrt x + 6}} - \frac{{\sqrt x + 3}}{{\sqrt x - 2}} - \frac{{2\sqrt x + 1}}{{3 - \sqrt x }}\).

a. Rút gọn A.

b. Tìm x để A < 1.

Phân tích đa thức sau thành nhân tử: x\(^2\)– 6x – 7.

Chứng minh phương trình sau có nghiệm: \({x^3} - 2x - 1 = 0\).

Cho ∆ABC có CB = 2, CA = 3 và \(\widehat {ACB} = 90^\circ \). Tính độ dài cạnh AB.

Tìm GTLN của hàm số y = 6sin2x – 8cos2x – 2.

Giải phương trình sau: \({\cos ^2}2x = \frac{1}{4}\).

Giải phương trình: cos2x – 3cosx + 2 = 0.

Giải phương trình: \({\cos ^2}x + 3\cos x + 2 = 0\).

Giải phương trình: cos4x + cos2x + 1 = 0.

Giải phương trình: 1 + cos4x = cos2x.

Giải phương trình tanx = cotx.

Giải phương trình: \(2{\sin ^2}x + \sin x\cos x - {\cos ^2}x = 0\).

Giải phương trình: \(2{\sin ^2}x - \sin x\cos x - {\cos ^2}x = 2\).

Cho một số có ba chữ số biết rằng khi viết thêm chữ số 5 vào bên phải số đó thì số đó tăng thêm 2444 đơn vị. Tìm số đó.

Giải phương trình: \({x^2} - {y^2} + 2x - 4y - 10 = 0\) với x, y nguyên dương.

Giải phương trình: sinx = cos3x.

Tia đối của tia NM là ?

Chứng minh: \(\left( {{n^4} - 14{n^3} + 71{n^2} - 154n + 120} \right)\,\, \vdots \,\,24\).

Giải phương trình: \(2{x^2} - 2x - 3 = 0\).

Phân tích đa thức thành nhân tử: \(4{a^2}{b^2} - {\left( {{a^2} + {b^2} - {c^2}} \right)^2}\).

Cho \(A = 4{a^2}{b^2} - \left( {{a^2} + {b^2} - {c^2}} \right)\). Trong đó a, b, c là độ dài 3 cạnh của 1 tam giác. Chứng minh A > 0.

Với mọi số thực a, b, c. Chứng minh rằng: \({a^2} + 5{b^2} - 4ab + 2a - 6b + 3 > 0\).

Cho a, b, c > 0 và a + b + c = 1. Chứng minh \(\sqrt {4a + 1} + \sqrt {4b + 1} + \sqrt {4c + 1} < 5\).

Cho ∆ABC có \(\frac{5}{{\sin A}} = \frac{4}{{\sin B}} = \frac{3}{{\sin C}}\) và a = 10. Tính chu vi tam giác.

Cho ∆ABC có các góc thỏa mãn \(\frac{{\sin A}}{1} = \frac{{\sin B}}{2} = \frac{{\sin C}}{3}\). Tính số đo các góc của tam giác.

Cho ∆ABC cân tại B, AB = a, đường trung tuyến BM. Gọi I là trung điểm của BC, E là điểm đối xứng với M qua I.

a. Tứ giác MCEB là hình gì?

b. Chứng minh tứ giác ABEM là hình bình hành.

c. Tìm điều kiện của ∆ABC để tứ giác MCEB là hình vuông.

Cho ∆ABC vuông tại A, M là trung điểm của BC, D, E lần lượt là hình chiếu của M trên AB và AC.

a) Tứ giác ADME là hình gì, tại sao?

b) Chứng minh DE = \(\frac{1}{2}\)BC.

c) Gọi P là trung điểm của BM, Q là trung điểm của MC, chứng minh tứ giác DPQE là hình bình hành. Từ đó chứng minh: tâm đối xứng của hình bình hành DPQE nằm trên đoạn AM.

d) Tam giác vuông ABC ban đầu cần thêm điều kiện gì để hình bình hành DPQE là hình chữ nhật?

Gọi M là điểm bất kì trên đoạn thẳng AB. Vẽ về một phía của AB các hình vuông AMCD, BMEF.

a) Chứng minh rằng AE ⊥ BC.

b) Gọi H là giao điểm của AE và BC Chứng minh rằng ba điểm D,H, F thẳng hàng.

c) Chứng minh rằng đường thẳng DF luôn luôn đi qua một điểm cố định khi điểm M chuyển động trên đoạn thẳng AB cố định.

Chứng minh BĐT: \({a^2} + {b^2} + {c^2} \ge ab + bc + ca\).

Giải phương trình: sin2x.cotx = 0.

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−2017; 2017] để hàm số \(y = \left( {{m^2} - 4} \right)x + 2m\) đồng biến trên ℝ.

Cho 10 chữ số 0, 1, 2, 3,..., 9. Có bao nhiêu có tự nhiên lẻ gồm 6 chữ số khác nhau, nhỏ hơn 600000 được xây dựng từ 10 số trên.

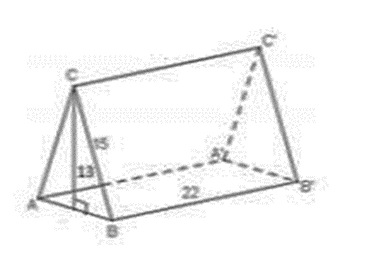
Một cục chặn giấy bằng sắt (hình vẽ) có dạng một lăng trụ đứng có chiều cao 22 cm, đáy là một tam giác cân (∆CAB) có chiều cao là 13 cm, cạnh bên dài 15 cm.

a. Tính độ dài cạnh AB(làm tròn đến phần trăm).

b. Tính diện tích phần sơn phủ cục chặn giấy (làm tròn đến\(c{m^3}\)).

Cho ∆ABC cân tại A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE.

a. Chứng minh rằng BE= CD.

b. Chứng minh rằng \(\widehat {ABE} = \widehat {ACD}\).

 c. Gọi K là giao điểm của BE và CD. ∆KBC là tam giác gì? Vì sao?

Một đoạn dây dẫn được uốn thành hình chữ nhật, có các cạnh a = 16 cm, b = 30 cm, trong đó có dòng điện cường độ I = 6A chạy qua. Xác định cảm ứng từ tại tâm hình chữ nhật ?

Một đội công nhân có 25 người nhận sửa xong một quãng đường trong 9 ngày. Hỏi muốn làm xong quãng đường đó trong 5 ngày thì cần thêm bao nhiêu người ?(mức làm của mỗi người như nhau).

Phân tích đa thức sau thành nhân tử: \({x^2} - 4{y^2} - x - 2y\).

Phân tích đa thức sau thành nhân tử: \({x^3} + 2{x^2} - 2{y^2} + {y^3}\).

Chứng minh: \({\sin ^4}x + {\cos ^4}x = 1 - 2{\sin ^2}x{\cos ^2}x\).

Tìm hệ số \({x^2}\) trong khai triển \({\left( {1 - 2x} \right)^8}\).

Trung bình cộng của 2 số là 138. Biết số thứ nhất là số lẻ nhỏ nhất có 3 chữ số. Tìm số thứ 2.

Trên khoảng \(\left( {\frac{\pi }{2};2\pi } \right)\), phương trình \(\cos \left( {\frac{\pi }{6} - 2\pi } \right) = \sin x\) có bao nhiêu nghiệm ?

Tìm tất cả các giá trị của tham số m để phương trình \(\left( {m + 1} \right)\sin x + 2 - m = 0\) có nghiệm ?

Tìm tọa độ giao điểm của đường thẳng (d) : x – 5y + 6 = 0 và trục hoành.

Giải BPT: \({x^2} - 8x + 16 < 0\).

Hãy tính dãy số sau đây: 1 + 2 + 3 +....+ 99 ?

Cho đường thẳng d₁ cắt Ox tại (–4; 0), cắt Oy tại (0, 2). Tìm ảnh của đường thẳng d₁ qua phép tịnh tiến theo vectơ \(\overrightarrow u = \left( {0;3} \right)\).

Tìm m để hàm số \(y = \frac{{{x^2} - 2mx + 2}}{{x - m}}\) đạt cực tiểu tại x = 2.

Giải phương trình: (1+sin²x)cosx + (1+ cos²x)sinx = 1 +sin2x

Chứng minh rằng: \(\frac{{1 + \cot x}}{{1 - \cot x}} = \frac{{\tan x + 1}}{{\tan x - 1}}\).

Cho \(\cos x = \frac{2}{{\sqrt 5 }},0 < x < \frac{\pi }{2}\). Tính các giá trị lượng giác của góc x.

Tìm tập giá trị của hàm số y = 2cosx.

Tìm GTLN và GTNN của hàm số y = 2cosx + \(\sqrt 2 \).

Cho ∆ABC nhọn, đường cao AK.

a. Giải ∆ACK biết \(\widehat C = 30^\circ \), AK = 3 cm.

b. Chứng minh \(AK = \frac{{BC}}{{\cot B + \cot C}}\).

c. Biết BC = 5 cm, \(\widehat B = 68^\circ ,\widehat C = 30^\circ \). Tính diện tích ∆ABC.

Cho ∆ABC với các cạnh AB = c, BC = a, AC = b, G là trọng tâm. Chứng minh \(G{A^2} + G{B^2} + G{C^2} = \frac{1}{3}\left( {{a^2} + {b^2} + {c^2}} \right)\).

Cho ∆ABC vuông tại A, đường cao AH. Vẽ đường tròn tâm A, bán kính AH, kẻ các tiếp tuyến BD, CE với đường tròn tâm A (D, E là các tiếp điểm khác H). Chứng minh rằng:

a. 3 điểm D, A, E thẳng hàng.

b. DE tiếp xúc với đường tròn có đường kính BC.

Đồ thị hàm số y = cos\(\left( {x - \frac{\pi }{2}} \right)\) được suy từ đồ thị (C) của hàm số y = cosx bằng cách nào ?

Cho tam giác nhọn ABC. Vẽ đường tròn (O) có đường kính BC, nó cắt cạnh AB, AC theo thứ tự ở D và E.

a. Chứng minh rằng CD ⊥ AB, BE ⊥ AC.

b. Gọi K là giao điểm của BE, CD. Chứng minh AK ⊥ BC.

Tìm nghiệm âm lớn nhất của phương trình \(\cot x = \tan \left( {\frac{x}{2} - \frac{\pi }{2}} \right)\).

Số nghiệm của phương trình sin2x – cos2x = 3sinx + cosx – 2 thuộc \(\left( {0;\frac{\pi }{2}} \right)\).

Cho tana = 2. Tính giá trị của biểu thức \(C = \frac{{\sin a}}{{{{\sin }^3}a + 2{{\cos }^3}a}}\).

Cho \(\left( {x + \sqrt {{x^2} + 1} } \right)\left( {y + \sqrt {{y^2} + 1} } \right) = 1\). Tính x + y ?

Cho 2 số thực x, y thỏa mãn \(\left( {x + \sqrt {{x^2} + 1} } \right)\left( {y + \sqrt {{y^2} + 1} } \right) = 1\). Tìm GTNN của biểu thức \(M = 10{x^4} + 8{y^4} - 15xy + 6{x^2} + 5{y^2} + 2017\).

Cho nửa khoảng \(A = \left[ {3;6} \right)\) và đoạn \(B = \left[ {m;m + 2} \right].\) Tìm tất cả các số thực m để \(A \cap B = \emptyset \).

Cho 2 khoảng A = \(\left( {m;m + 1} \right)\) và \(B = \left( {3;5} \right)\). Tìm tất cả các số thực m để \(A \cap B\) là 1 khoảng.

Cho hình bình hành ABCD. E, F lần lượt là trung điểm của AB và CD.

a. Tứ giác DEBF là hình gì? Vì sao?

b. Chứng minh 3 đường thẳng AC, BD, EF đồng quy.

c. Gọi giao điểm của AC với DE và BF theo thứ tự là M, N. Chứng minh tứ giác EMFN là hình bình hành.

Tìm tất cả các giá trị x ∈ ℕ thỏa mãn \(6\left( {{P_x} - {P_{x - 1}}} \right) = {P_{x + 1}}\).

Xác định các hằng số a, b sao cho \({x^4} + ax + b\) chia hết cho \({x^2} - 4\).

Cho đường tròn (O; R) đường kính AB. Kẻ tiếp tuyến Ax, lấy P trên Ax (AP > R). Từ P kẻ tiếp tuyến PM với (O).

a, Chứng minh bốn điểm A, P, M, O cùng thuộc một đường tròn.

b, Chứng minh BM // OP.

c, Đường thẳng vuông góc với AB tại O cắt tia BM tại N. Chứng minh tứ giác OBNP là hình bình hành.

d, Giả sử AN cắt OP tại K; PM cắt ON tại I; PN cắt OM tại J. Chứng minh I, J, K thẳng hàng.

Gọi M; N lần lượt là trung điểm các cạnh AD; BC của tứ giác ABCD. Đẳng thức nào sau đây sai?

Cho hình bình hành ABCD. Đẳng thức nào sau đây đúng?

Cho ABCD là hình bình hành. Chứng minh \(\overrightarrow {MB} - \overrightarrow {MA} = \overrightarrow {MC} - \overrightarrow {MD} \).

Cho hình bình hành ABCD và 1 điểm M tùy ý. Chứng minh rằng

\(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \).

Tìm tất cả các giá trị của tham số m để hàm số

y = \(\frac{1}{3}{x^3} + \left( {m - 1} \right){x^2} + \left( {2m - 3} \right)x - \frac{2}{3}\) đồng biến trên \(\left( {1; + \infty } \right)\).

Cho ∆ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, AC, BC. Hỏi \(\overrightarrow {MP} + \overrightarrow {NP} \) bằng vectơ nào?

Cho ∆ABC. Khẳng định nào sau đây là đúng ?

Cho hình thang vuông ABCD có \(\widehat B = \widehat C = 90^\circ \) và \(AB = BC = \frac{1}{2}CD = 2cm\). Tính độ dài đường chéo và cạnh bên của hình thang.

Cho ∆ABC nhọn nội tiếp đường tròn (O, R). Biết AB = \(R\sqrt 3 \) , AC = \(R\sqrt 2 \) . Tính các góc tam giác đó.

Cho ∆ABC vuông tại A có AB = 12cm, AC = 16cm, vẽ đường cao AH.

a, Chứng minh: ∆HBA ∆ABC.

b, Tính BC.AH.

c, Trong ∆ABC, kẻ phân giác AD (D ∈BC). Trong ∆ADB kẻ phân giác DE (E ∈ AB). Trong ∆ADC kẻ phân giác DF(F ∈ AC). Chứng minh: \(\frac{{EA}}{{EB}}.\frac{{DB}}{{DC}}.\frac{{FC}}{{FA}} = 1\) .

Giải phương trình nghiệm nguyên: \(2{x^2} + {y^2} - 2xy - 2x + y = 4\).

Tính \(\sqrt {7 - 2\sqrt 6 } \).

So sánh các góc của ∆ABC biết rằng AB = BC = 5 cm, AC = 3 cm.

∆ABC có AB = 2 cm, AC = 1 cm, \(\widehat A = 60^\circ \). Tính độ dài cạnh BC.

Cho \(P = \left( {1 - \frac{{\sqrt x }}{{\sqrt x + 1}}} \right):\left( {\frac{{\sqrt x + 3}}{{\sqrt x - 2}} + \frac{{\sqrt x + 2}}{{3 - \sqrt x }} + \frac{{\sqrt x + 2}}{{x - 5\sqrt x + 6}}} \right)\) với x ≥ 0; x ≠ 4; x ≠ 9.

a. Rút gọn P.

b. Tìm x ∈ ℤ để P ∈ ℤ.

Tính tổng B = 2 + \({2^3} + {2^5} + {2^7} + ... + {2^{2009}}\).

Tính \(\sqrt {4 - \sqrt 7 } - \sqrt {4 + \sqrt 7 } \).

Tìm x, biết \(2{x^2} + 5x - 3 = 0\).

Tìm mẫu chung và rút gọn biểu thức \(y = \frac{{5 + 2\sqrt 5 }}{{\sqrt 5 }} - \frac{1}{{\sqrt 5 - 2}}\).

Tính \(A = \left( {\sqrt 5 - 2} \right)\left( {\sqrt 5 + 2} \right)\).

Cho ∆ABC vuông tại A có đường cao AH. Kẻ HE, HF vuông góc với AB, AC. Chứng minh rằng: \(\frac{{EB}}{{FC}} = \frac{{A{B^3}}}{{A{C^3}}}\).

Cho ∆ABC nhọn, đường cao AH. Kẻ HD ⊥ AB, HE ⊥ AC.

a.Chứng minh AD.AB = AE.AC.

b. Chứng minh \(\frac{{AD}}{{BD}} = \frac{{A{H^2}}}{{B{H^2}}}\).

Cho ∆MNP. Gọi D, E, F lần lượt là trung điểm của MN, NP, PM.

a. Chứng minh tứ giác MDEF là hình bình hành.

b. ∆MNP có điều kiện gì thì tứ giác MDEF là hình chữ nhật.

Giải phương trình \(\cos 3x = \cos \frac{\pi }{{15}}\).

Cho ∆ABC nhọn, 2 đường trung tuyến BM và CN cắt nhau tại I. Gọi E và F là trung điểm của IB và IC.

a. Chứng minh tứ giác MNEF là hình bình hành.

b. BC cắt NE và MF tại H và K. Chứng minh \(CM.HK = \frac{{BC}}{2}\).

Cho ∆ABC vuông tại A (AB < AC), đường cao AH. Trên cạnh BC lấy điểm M sao cho BA = BM.

a) Chứng minh AM là tia phân giác của \(\widehat {HAC}\).

b) Gọi K là hình chiếu vuông góc của M trên AC. Chứng minh AM là trung trực của HK.

c) Gọi I là hình chiếu vuông góc của C trên tia AM. Chứng minh AH, KM, CI đồng quy.

d) Chứng minh AB + AC < AH + BC.

Giải phương trình: \({x^2}\) – 5x + 6 = 0.

Cho ∆ABC có AB = 2, AC = 3, \(\widehat A = 60^\circ \). Tính độ dài phân giác \(\widehat A\).

Cho các điểm A(1; –2), B(–2; 3), C(0; 4). Tính diện tích ∆ABC.

Nghiệm bội lẻ là gì ?

Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm.

a) Tính khoảng cách từ tâm O đến dây AB.

b) Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD đi qua I và vuông góc với AB. Chứng minh rằng CD = AB.

Nhận dạng ∆ABC trong trường hợp sau: \(\frac{a}{{\cos A}} = \frac{b}{{\cos B}}\).

Phân tích đa thức sau thành nhân tử: \({x^4}\left( {y - z} \right) + {y^4}\left( {z - x} \right) + {z^4}\left( {x - y} \right)\).

Mệnh đề nào sau đây đúng ?