5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 34)

Cho hình chữ nhật ABCD tâm O, AB = 12a, AD = 5a. Tính \(\left| {\overrightarrow {AD} - \overrightarrow {AO} } \right|\).

Cho hình chữ nhật ABCD tâm O có: AD = a, AB = 2a. Tính \(\overrightarrow {AB} \,.\,\overrightarrow {AO} \).

Cho tam giác ABC với A = (2; 3), B = (–1; 4), C = (1; 1). Tìm các tọa độ của đỉnh D của:

a) Hình bình hành ABCD;

b) Hình bình hành ACBD.

Cho tam giác ABC có AB = AC và D là trung điểm của BC. Gọi E là trung điểm của AC, trên tia đối của tia EB lấy điểm M sao cho EM = EB.

a) Chứng minh ∆ABD = ∆ACD;

b) Chứng minh rằng AM = 2.BD;

c) Tính số đo \(\widehat {MAD}\).

Cho \(\cos \alpha = \frac{4}{5}\) với 0 < α < \(\frac{\pi }{2}\). Tính sinα.

Tìm A ∪ B ∪ C, A ∩ B ∩ C với:

a) A = [1 ; 4], B = (2; 6), C = (1; 2);

b) A = [ 0; 4], B = (1; 5), C = (–3; 1];

c) A = ( –5; 1], B = [3; +∞), C = ( –∞; – 2).

Rút gọn và tính giá trị của các biểu thức sau:

a) A = (3x + 5)(2x – 1) – (1 – 4x)(3x + 2) tại \(\left| x \right| = 2\);

b) B = (2x + y)(2x – y) + xy(x – y) – xy(x + y) tại x = 0; y = –1.

Một thửa ruộng hình chữ nhật có chiều dài 60 m, chiều dài bằng \(\frac{3}{2}\) chiều rộng. Trên thửa ruộng đó người ta trồng lúa cứ 100 m² thu hoạch được 50 kg. Hỏi trên cả thửa ruộng thu hoạch được bao nhiêu tạ thóc?

Một trường trung học phổ thông có 4 học sinh giỏi khối 12, có 5 học sinh giỏi khối 11, có 6 học sinh giỏi khối 10. Hỏi có bao nhiêu cách sắp xếp 15 học sinh trên thành một hàng ngang để đón đoàn đại biểu, nếu các học sinh ở cùng một khối thì xếp gần nhau.

Số các số tự nhiên có 5 chữ số khác nhau và chia hết cho 10 là:

Tìm một số biết rằng gấp số đó lên 2,5 lần rồi trừ đi 1,6 thì được 5,4

Chứng minh: \(\overrightarrow {AB} - \overrightarrow {CD} = \overrightarrow {AC} - \overrightarrow {BD} \)

Tìm giá trị lớn nhất (hoặc nhỏ nhất) của các biểu thức sau: A =  x² − 6x + 11

Viết biểu thức x³ – 6x² + 12x – 8 dưới dạng lập phương của một hiệu:

Xác định parabol y = ax² + bx + 2, biết rằng parabol đó: Có đỉnh là I(2; – 2)

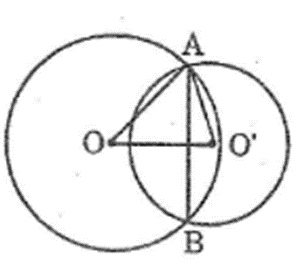
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B như hình bên. Biết OA = 15 cm, O’A = 13 cm, AB = 24 cm. Tính độ dài OO’.

Trong không gian hệ tọa độ Oxyz cho mặt phẳng (P): x – y + 2z – 2 = 0 và 2 điểm A (2; 3; 0); B (2; – 1; 2). Tìm điểm M thuộc mặt phẳng (P) sao cho \(\left| {MA - MB} \right|\) lớn nhất.

Trong mặt phẳng Oxy, cho tam giác ABC biết A (–2; –3), B (1; 1). Tìm điểm M trên trục Oy sao cho \(\left| {MA - MB} \right|\) lớn nhất.

Giải phương trình \(\sqrt {x + 1} + 1 = 4{x^2} + \sqrt {3x} \)

Cho đường tròn (O) và tiếp tuyến AB (B là tiếp điểm). Lấy điểm C thuộc đường tròn (O) sao cho AB = AC. Chứng minh C là tiếp tuyến của đường tròn (O).

Từ một điểm A nằm ngoài đường tròn (O; R) kẻ tiếp tuyến AB với (O) (B là tiếp điểm). Đường thẳng đi qua B vuông góc với OA tại H và cắt đường tròn (O) tại C. Vẽ đường kính BD. Đường thẳng AO cắt đường tròn (O) tại hai điểm M và N (M nằm giữa A và N). Chứng minh:

a) CD // OA.

b) AC là tiếp tuyến của đường tròn (O).

c) Cho biết R = 15 cm, BC = 24 cm. Tính AB, OA.

Tìm m để 3 đường thẳng y = −5(x + 1), y = mx + 3, y = 3x + m phân biệt và đồng quy

Trong trường hợp sau, tìm các giá trị của m sao cho 3 đường thẳng sau phân biệt và đồng quy

y = 2x; y = −x + 3; y = mx + 5

Cho hình chữ nhật ABCD có AB = 12 cm, BC = 5 cm. Tính bán kính đường tròn đi qua bốn đỉnh A, B, C, D.

Tính bán kính đường tròn ngoại tiếp hình chữ nhật

Cho tam giác ABC, AB = AC. Tia phân giác của góc A cắt BC tại M.

a) Chứng minh: ∆AMB = ∆AMC.

b) Chứng minh M là trung điểm của cạnh BC.

c) K là một điểm bất kì trên đoạn thẳng AM, đường thẳng CK cắt cạnh AB tại I. Vẽ IH vuông góc với BC tại H. Chứng minh \(\widehat {BAC} = 2\widehat {BIH}\).

Cho ∆ABC, có AB = AC. Tia phân giác của góc A cắt BC tại M. Chứng minh M là trung điểm của cạnh BC.

Chứng minh rằng: Nếu \(\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = 2\) và a + b + c = abc thì \(\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}} = 2\).

Tìm điều kiện để phép chia là phép chia hết:

a) xⁿyⁿ⁺¹ : x²y⁵;

b) (13x⁴y³ – 5x³y³ + 6x²y²) : 5xⁿyⁿ.

Cho hàm số \(y = \frac{1}{2}{x^2}\).

a) Vẽ đồ thị (P) của hàm số.

b) Tìm trên (P) những điểm cách đều hai trục tọa độ (không trùng với O).

c) Tìm trên (P) những điểm có tung độ bằng \(\frac{9}{2}\).

Cho hàm số y = 2x + 3 và \(y = \frac{{ - 1}}{2}x - 2\).

a) Vẽ đồ thị hàm số trên cùng 1 mặt phẳng tọa độ.

b) Tìm tọa độ của điểm C của 2 đồ thị trên.

c) Tính diện tích tam giác ABC biết A, B lần lượt là giao điểm của 2 đường thẳng trên trục tung.

Cho hai hàm số: y = 2x – 3 và \(y = \frac{{ - 1}}{2}x + 2\) có đồ thị lần lượt là các đường thẳng (d₁) và (d₂).

a) Vẽ trên cùng một hệ trục tọa độ các đường thẳng (d₁) và (d₂).

b) Tìm tọa độ giao điểm hai đường thẳng (d₁) và (d₂) bằng phép toán.

c) Tính góc tạo bởi đường thẳng (d₁) và trục Ox.

Vẽ đồ thị hàm số y = x² − 3x + 2

Vẽ đường parabol sau: y = −2x² + 2x + 3

Xác định a, b, c biết parabol y = ax² + bx + c đi qua điểm A (8; 0) và có đỉnh là I (6; −12).

Cho hai hàm số y = −x + 3 và y = 3x − 1 có đồ thị lần lượt là hai đường thẳng d₁ và d₂.

a) Vẽ d₁ và d₂ trên cùng một hệ trục tọa độ.

b) Tính góc tạo bởi d₁, d₂ và trục Ox (làm tròn đến độ).

d) Tính khoảng cách từ O đến d₁, d₂.

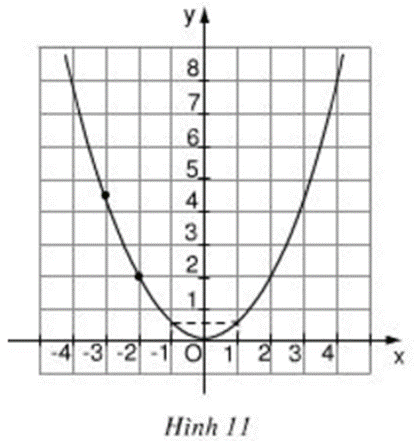
Biết rằng đường cong trong hình 11 là một parapol y = ax².

Tìm các điểm thuộc parapol có tung độ y = 8.

Tìm tập xác định của hàm số \(y = \frac{3}{{\sin x}}\):

Cho nửa đường tròn tâm O bán kính R đường kính AB. Gọi Ax, By là các tia tiếp tuyến của nửa đường tròn và thuộc cùng 1 nửa mặt phẳng có chứa nửa đường tròn qua M thuộc nửa đường tròn vẽ tiếp tuyến với nửa đường với nửa đường tròn cắt Ax, By lần lượt tại C, D.

a) Chứng minh rằng CD = AC + BD, \(\widehat {COD} = 90^\circ \)

b) AC.BD = R²

c) Chứng minh AB là tiếp tuyến của đường tròn, đường kính CD

d) AD cắt BC tại N, MN cắt AB tại K. Chứng minh rằng: MN // AC

Cho nửa đường tròn tâm O với bán kính R, đường kính AB. Trên nửa mặt phẳng bờ là đường thẳng AB chứa nửa đường tròn, kẻ tiếp tuyến Ax tại A của nửa đường tròn. Xét điểm M thay đổi trên Ax, không trùng với A. Gọi E là điểm đối xứng với A qua OM.

a) Chứng minh rằng ME là một tiếp tuyến của nửa đường tròn (O)

b) Đoạn OM cắt nửa đường tròn (O) tại I. Chứng minh rằng I là tâm đường tròn nội tiếp của tam giác AME

c) Gọi N là trung điểm EB. Tia ME cắt ON tại P. Hãy xác định vị trí của điểm M trên tia Ax để diện tích tam giác OMP đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó theo R.

c) Gọi C là giao điểm của BE và tia Ax, OC cắt AE tại Q. Kẻ đường thẳng qua Q và song song với Ax, cắt OM tại D. Chứng minh rằng A, D, P thẳng hàng.

Cho parabol (P): \(y = \frac{1}{2}{x^2}\) và đường thẳng (d): \(y = mx - \frac{1}{2}{m^2} + m + 1\). Tìm các giá trị của m để (P) và (d) cắt nhau tại 2 điểm phân biệt có hoành độ x₁, x₂ sao cho |x₁ − x₂| = 2

Cho parabol (P): \(y = \frac{1}{2}{x^2}\) và đường thẳng (d): y = mx + 2.

a) Chứng minh rằng với mọi giá trị của m đường thẳng (d) luôn cắt parabol (P) tại 2 điểm phân biệt.

b) Gọi x₁, x₂ lần lượt là hoành độ các giao điểm của đường thẳng (d) và parabol (P). Tìm giá trị của m để \[\frac{{{x_1}}}{{{x_2}}} + \frac{{{x_2}}}{{{x_1}}} = - 3\]

Cho tam giác ABC. Tập hợp các điểm thỏa mãn \(\left| {\overrightarrow {MB} - \overrightarrow {MC} } \right| = \left| {\overrightarrow {BM} - \overrightarrow {BA} } \right|\)là

Cho ∆ABC cân tại A. H là trung điểm của BC. D là hình chiếu của H trên AC, M là trung điểm của HD. Chứng minh AM vuông góc BD.

Cho tam giác ABC cân tại A, M trung điểm BC, H là hình chiếu của M trên AC, E là trung điểm MH . Chứng minh AE vuông góc với BH

Cho tam giác ABC cân tại A. Trên tia đối của tía AC lấy điểm D. Trên tia đối của tia AB lấy điểm E sao cho AD = AE. Chứng minh DECB là hình thang cân.

Cho tam giác ABC cân tại A. Trên tia đối của tía AC lấy điểm D. Trên tia đối của tia AB lấy điểm E sao cho AD = AE. Chứng minh:

a) DE // BC

b) BE = CD

c) ∆BED = ∆CDE

Cho tam giác ABC có AM là trung tuyến, I là trung điểm AM

a) Chứng minh: \(2\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \)

b) Với O bất kỳ, chứng minh: \(2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 4\overrightarrow {OI} \)

Cho tam giác ABC có trung tuyến AM, gọi I là trung điểm AM. Đẳng thức nào sau đây đúng?

Cho tam giác ABC có AB < AC. AH là đường cao. Gọi M, N, K lần lượt là trung điểm của AB, AC, BC.

a) Chứng minh: MNKH là hình thang cân

b) Trên AH và AK lần lượt lấy điểm E và D sao cho H là trung điểm của AE và K là trung điểm của AD. Chứng minh tứ giác BCDE là hình thang cân

Cho tam giác ABC nhọn (AB < AC). Gọi M, N, K lần lượt là trung điểm của AB, AC, BC. Đường cao AH

a) Chứng minh tứ giác MNKH là hình thang cân

b) Gọi E là điểm đối xứng của M qua N. Tứ giác AMCE là hình gì?

c) Tam giác ABC cần có thêm điều kiện gì thì tứ giác AECM là hình chữ nhật?

Cho △ABC cân tại B có đường cao BE. Trên tia đối của tia EB lấy điểm D sao cho ED = EB. Chứng minh: tứ giác ABCD là hình thoi.

Cho tam giác ABC cân tại B có đường cao BE. Trên tia đối của tia EB lấy điểm D sao cho ED = EB. Chứng minh:

a) Tứ giác ABCD là hình bình hành.

b) Tứ giác ABCD là hình thoi.

Cho đường thẳng (d) có phương trình y = (3m – 2)x + m – 2 (với m là tham số)
a) Tìm giá trị của m biết đường thẳng (d) đi qua điểm A(1; 2). Vẽ đồ thị hàm số với m tìm được

b) Đường thẳng (d) cắt Ox tại A, Oy tại B. Tìm m để diện tích ∆OAB bằng \(\frac{1}{2}\).

Cho đồ thị (d): y = (3m − 2)x + m − 2 với m là tham số

a) Tìm điểm cố định mà d luôn đi qua mọi giá trị của m

b) Tìm m để khoảng cách từ gốc tọa độ đến d lớn nhất

Cho đường tròn (O; R) và một điểm A ở ngoài đường tròn. Vẽ các tiếp tuyến AB, AC. Chứng minh rằng \(\widehat {BAC} = 60^\circ \) khi và chỉ khi OA = 2R

Chứng minh đẳng thức:

\(\frac{{{x^2} + 3xy}}{{{x^2} - 9{y^2}}} + \frac{{2{x^2} - 5xy - 3{y^2}}}{{6xy - {x^2} - 9{y^2}}} = \frac{{{x^2} + xz + xy + yz}}{{3yz - {x^2} - xz + 3xy}}\)

Tính nhanh \(\frac{{{x^2} - 6xy + 9{y^2}}}{{3y - x}}\).

Gieo một con súc sắc cân đối đồng chất hai lần. Tính xác suất của biến cố:

a) Tổng số chấm hai mặt xuất hiện bằng 8.

b) Tích số chấm hai mặt xuất hiện là số lẻ.

Gieo một con xúc xắc cân đối đồng chất 2 lần, tính xác suất để biến cố có tích 2 lần số chấm khi gieo xúc xắc là một số chẵn.

Giải bất phương trình sau: 3x² – 4x + 4 > 0.

Giải bất phương trình sau: – 3x² + x + 4 ≥ 0.

Cho hàm số y = f(x) = ax².

a) Xác định a biết rằng khi x = 2 thì y = – 2.

b) Vẽ đồ thị (P) của hàm số với a tìm được.

Cho hàm số y = f(x) = ax² – 2.

a) Hãy xác định a biết f(3) =16;

b) Tính f(2), f(– 2), f(0), f(1), f(– 1).

Cho tam giác ∆ABC chứng minh rằng:

a) \(\sin \left( {\frac{{\widehat A + \widehat B}}{2}} \right) = \cos \frac{{\widehat C}}{2}\);

b) \(\tan \left( {2\widehat A + \widehat B + \widehat C} \right) = \tan \widehat A\);

c) \(\sin \left( {\frac{{\widehat A + \widehat B + 3\widehat C}}{2}} \right) = \cos \widehat C\).

Chứng minh rằng:

a) \(\sin \alpha + \cos \alpha = \sqrt 2 \cos \left( {\alpha - \frac{\pi }{4}} \right) = \sqrt 2 \sin \left( {\alpha + \frac{\pi }{4}} \right)\);

b) \(\sin \alpha - \cos \alpha = \sqrt 2 \sin \left( {\alpha - \frac{\pi }{4}} \right) = - \sqrt 2 \cos \left( {\alpha + \frac{\pi }{4}} \right)\).

Cho tam giác ABC vuông tại C (AC < BC), đường cao CK và đường phân giác trong BD (K Î AB, D Î AC). Qua D kẻ đường thẳng vuông góc với AC cắt CK, AB lần lượt tại H và I.

a) Chứng minh CDKI là tứ giác nội tiếp.

b) Chứng minh AD.AC = DH.AB

c) Gọi F là trung điểm AD. Đường tròn tâm I bán kính ID cắt BC tại M (M khác B) và cắt AM tại N (N khác M). Chứng minh B, N, F thẳng hàng.

Cho tam giác ABC vuông tại C (AC < BC), đường cao CHK và đường phân giác trong BD (H Î AB, D Î AC). Qua D kẻ đường thẳng vuông góc với AC cắt CH, AB lần lượt tại E và F.

a) Chứng minh bốn điểm C, D, H, F cùng thuộc một đường tròn.

b) Chứng minh AD.AC = DE.AB

Tìm x, biết: x + 456,95 × 8 = 5248.