5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 31)

Cho hình chóp S.ABCD, đáy là hình thang có đáy lớn là AB. Gọi M, N lần lượt là trung điểm của SA, SB.

a) Chứng minh MN // CD.

b) Tìm giao điểm P của SC và (AND).

c) Gọi I là giao điểm của AN và DP. Chứng minh SI // AB // CD.

Cho hình chóp đỉnh S có đáy là hình thang ABCD với AB là đáy lớn. Gọi M, N theo thứ tự là trung điểm của các cạnh SB và SC.

a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).

b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN).

c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN).

Kết quả điều tra ở một lớp học cho thấy: Có 20 học sinh thích bóng đá, 17 học sinh thích bơi, 36 học sinh thích bóng chuyền, 14 học sinh thích đá bóng và bơi, 13 học sinh thích bơi và bóng chuyền, 15 học sinh thích bóng đá và bóng chuyền, 10 học sinh thích cả ba môn, 12 học sinh không thích môn nào. Tính xem lớp học đó có bao nhiêu học sinh?

Xác định hàm số bậc nhất y = ax + b (a ≠ 0) biết rằng đồ thị của hàm số này song song với đường thẳng y = 2x + 3 và cắt trục hoành tại điểm có hoành độ là – 2.

Chứng minh các hệ thức

a) \(1 + {\tan ^2}a = \frac{1}{{{\rm{co}}{{\rm{s}}^2}a}}\);

b) \(1 + {\cot ^2}a = \frac{1}{{{\rm{si}}{{\rm{n}}^2}a}}\);

c) \(\frac{{\cos a}}{{1 - \sin a}} = \frac{{1 + \sin a}}{{\cos a}}\).

Cho biểu thức \(A = \frac{{x + 2}}{{x + 3}} - \frac{5}{{{x^2} + x - 6}} + \frac{1}{{2 - x}}\).

a) Tìm điều kiện để A có nghĩa (xác định).

b) Rút gọn A.

c) Tìm x để \(A = \frac{{ - 3}}{4}\).

d) Tìm x để biểu thức A nguyên.

e) Tính giá trị của A khi x² – 9 = 0.

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, \(\widehat {ABC} = {\rm{ }}60^\circ ,\;\) cạnh bên \(SB = a\sqrt 2 \) và SA vuông góc với ABCD. Tính góc giữa SB và (SAC).

Cho tam giác ABC có AM là trung tuyến, I là trung điểm AM.

a) Chứng minh:\(2\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \).

b) Với O bất kỳ , chứng minh: \(2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 4\overrightarrow {OI} \).

Giải phương trình: \[\sqrt[3]{{{{\left( {2 - x} \right)}^2}}} + \sqrt[3]{{{{\left( {7 + x} \right)}^2}}} - \sqrt[3]{{\left( {7 + x} \right)\left( {2 - x} \right)}} = 3\].

Cho x; y là 2 số không âm thỏa mãn x + y = 1. Chứng minh: \(\frac{x}{{y + 1}} + \frac{y}{{x + 1}} \le 1\).

Rút gọn \(3{\rm{x}} - \sqrt {{x^2} - 2{\rm{x}} + 1} \).

Số tự nhiên thích hợp để điền vào dãy số sau: 3, 17, 59, 185, 563, ... là số nào?

Phân tích các đa thức sau thành nhân tử:

a) 4x² – 4xy + y²;

b) 9x³ – 9x²y – 4x + 4y;

c) x³ + 2 + 3(x³ – 2).

Từ điểm A ở bên ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC đến đường tròn (O) (B, C là 2 tiếp điểm). Kẻ cát tuyến ADE với đường tròn (O) (D nằm giữa A và E). a) Chứng minh: bốn điểm A, B, O, C cùng thuộc một đường tròn. b) Chứng minh: OA⊥ BC tại H và OD² = OH. OA. Từ đó suy ra tam giác OHD đồng dạng với tam giác ODA. c) Chứng minh CB trùng với tia phân giác của góc DHE. d) Từ D kẻ đường thẳng song song với BE, đường thẳng này cắt AB, BC lần lượt tại M và N. Chứng minh: D là trung điểm của MN.

Cho tam giác ABC nhọn, BD vuông góc với AC, D thuộc AC, CE vuông góc với AB, E thuộc AB, BD cắt CE tại I. Chứng minh góc BIC bù góc A.

Cho tam giác ABC với AB = AC. Lấy I là trung điểm BC. Trên tia BC lấy điểm N, trên tia CB lấy điểm M sao cho CN = BM. Chứng minh:

a) \(\widehat {ABI} = \widehat {ACI}\)và AI là tia phân giác của góc BAC.

b) AM = AN.

c) AI vuông góc với BC.

Cho tam giác ABC với AB = AC. Lấy I là trung điểm BC. Trên tia BC lấy điểm N, trên tia CB lấy điểm M sao cho CN = BM. Chứng minh:

a) \(\widehat {ABI} = \widehat {ACI}\)và AI là tia phân giác của góc BAC.

b) AM = AN.

c) AI vuông góc với BC.

Cho tam giác ABC có 3 góc nhọn và AB < AC. Các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC. Trên tia đối của MH lấy điểm K sao cho HM = MK.a) Chứng minh: Tứ giác BHCK là hình bình hành. b) Chứng minh BK vuông góc AB và CK vuông góc AC.c) Gọi I là điểm đối xứng với H qua BC. Chứng minh: Tứ giác BIKC là hình thang cân. d) BK cắt HI tại G. Tam giác ABC phải có thêm điều kiện gì để tứ giác GHCK là hình thang cân.

Trung Bình cộng số vở của 2 bạn Hiền và Hương là 56 quyển. Số vở của Hiền ít hơn Trung bình cộng số vở của 2 bạn là 14 quyển vở. Vậy bạn Hương có nhiều hơn bạn Hiền bao nhiêu quyển vở?

Cho hình vuông ABCD. Trên cạnh các AD, DC lần lượt lấy các điểm E, F sao cho AE = DF. Gọi M, N lần lượt là trung điểm của EF, BF.

a) Chứng minh các tam giác ADF và BAE bằng nhau.

b) Chứng minh MN vuông góc AF.

Cho tam giác ABC. Tìm điểm M thỏa mãn\(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \).

Mẹ đi chợ về mua 10 lít nước mắm, trong đó có 4 lít nước mắm loại một, còn lại là nước mắm loại hai. Tỉ số phần trăm giữa nước mắm loại một và nước mắm loại hai là:

Một người bỏ ra 250 000 đồng (tiền vốn) để mua rau. Sau khi bán hết số rau này thì thu được 300 000 đồng. Hỏi người đó được lãi bao nhiêu phần trăm?

Cho biết \(\frac{{b{\rm{z}} - cy}}{a} = \frac{{c{\rm{x}} - az}}{b} = \frac{{ay - b{\rm{x}}}}{c}\). Chứng minh x : y : z = a : b : c.

Cho hình vuông ABCD. Trên tia đối của tia BA lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho AE = CF.

a) Chứng minh tam giác EDF vuông cân.

b) Gọi I là trung điểm của EF. Chứng minh BI = DI.

c) Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh O, C, I thẳng hàng.

Cho tam giác ABC. Vẽ điểm D thỏa mãn \(\overrightarrow {A{\rm{D}}} = \overrightarrow {BC} \). Tứ giác ABCD là hình gì?

Cho hình thang ABCD (AB // CD, AB < CD), hai tia phân giác của góc B và góc C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC cắt AB, CD lần lượt tại E và F. a) Chứng minh tam giác BEI cân tại E và tam giác IFC cân tại F. b) Chứng minh EF=BE+CF.

Giải phương trình lượng giác \(\sqrt 3 \sin x + cosx = 1\).

Phương trình \(\sqrt 3 \sin x - cosx = 1\) tương đương với phương trình nào sau đây?

Cho hai khoảng A = (m; m + 1) và B = (3; 5)

Tìm m để A ∪ B là một khoảng. Hãy xác định khoảng đó.

Cho đường tròn (O; 13) và một điểm M cách O là 5. Có bao nhiêu dây có độ dài là một số tự nhiên đi qua M ?

Giải phương trình sinx + cosx = 1.

Cho đường tròn tâm O bán kính R = 2,5 cm và dây AB di động, sao cho AB = 4 cm. Hỏi trung điểm H của AB di động trên đường nào?

Tìm GTNN của A = x⁴ – 2x³ + 3x² + 4x + 5.

Cho hình vuông ABCD tâm O, gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Phép dời hình biến DAMO thành DCPO là

Phương trình sinx = a luôn có nghiệm khi nào?

Một ô tô chạy 100km hết 13 lít xăng. Hỏi cần bao nhiêu xăng khi ô tô chạy quãng đường 300 000 m?

Di chuyển 1 que diêm để phép tính 2 + 3 – 8 = 4 có kết quả đúng: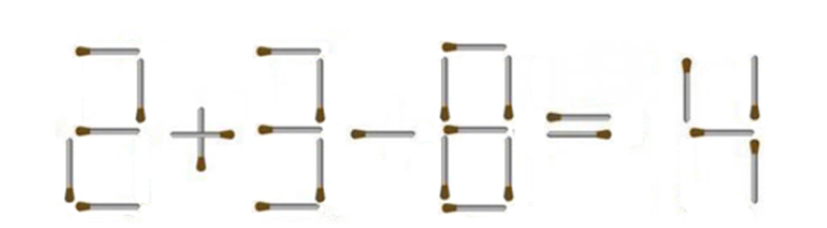

Chứng minh rằng trong mọi tam giác ABC ta đều có:

a) a = b cosC + c cosB;

b) sinA = sinBcosC + sinCcosB;

c) ha = 2RsinBsinC.

Cho A = 5 + 70 + x với x thuộc ℕ. Tìm x để:

a) A chia hết cho 5;

b) A không chia hết cho 5.

Cho H, K là các giao điểm  của đường tròn (O₁), (O₂). Đường thẳng O₁H cắt (O₁) tại A , (O₂) tại B . O₂H cắt (O₁)  tại C và (O₁) tại D. Chứng minh rằng ba đường thẳng  BC, BD, HK đồng quy tại 1 điểm.

Cho tam giác ABC cân tại A \(\left( {\widehat A < 90^\circ } \right)\), đường cao AH. Kẻ HK ⊥ AC (K ∈ AC).

a) Tính HC, HK, \(\widehat C\) nếu AH = 20 cm, AC = 25 cm.

b) Qua B kẻ đường thẳng song song với AH, đường thẳng này cắt AC tại điểm E. Kẻ BD ⊥ AC (D ∈ AC). Chứng minh \(B{H^2} = \frac{{C{\rm{D}}.CE}}{4}\).

c) Gọi O là giao điểm của BD và AH. Chứng minh \(\frac{{BO}}{{DO}} = \frac{{A{\rm{E}}}}{{A{\rm{D}}}}\).

d) Kẻ KF ⊥ BC (F ∈ BC). Chứng minh CF = AC. sin³E.

Cho tam giác ABC có các đường trung tuyến xuất phát từ B và C vuông góc với nhau. Chứng minh \[cosA \ge \frac{4}{5}\].

Cho tam giác ABC vuông tại A, đường cao AH. Qua H kẻ các đường thẳng song song với AB và AC lần lượt cắt AC tại E, AB tại D.

a) Chứng minh rằng: Tứ giác ADHE là hình chữ nhật.

b) Gọi M, N lần lượt là trung điểm của BH và CH. Biết AB = 6 cm; AC = 8 cm. Tính BC, DM, DM + EN?

c) Chứng minh rằng: Tứ giác DMNE là hình thang.

Cho tana = 2. Tính giá trị của biểu thức \(A = \frac{{4\sin a + 3\cos a}}{{5\sin a - 2\cos a}}\).

Cho tanα = – 2. Tính giá trị biểu thức \(A = \frac{{3c{\rm{os}}\alpha + 4\sin \alpha }}{{{\rm{cos}}\alpha + \sin \alpha }}\) .