5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 30)

Cho tam giác ABC có\(\widehat B = \widehat C\) . Tia phân giác của góc A cắt BC tại D.Chứng minh rằng:

a) Tam giác ADB bằng tam giác ADC

b) AB = AC.

Giải phương trình

a) sin5x + sin8x + sin3x= 0.                 

b) \[4co{s^3}x + \;3\sqrt 2 sin2x{\rm{ }} = {\rm{ }}8cosx.\]

Cho 5 điểm A, B, C, D, E. Chứng minh rằng: \(\overrightarrow {AC} + \overrightarrow {DE} - \overrightarrow {DC} - \overrightarrow {CE} + \overrightarrow {CB} = \overrightarrow {AB} .\)

Cho bảng biến thiên hàm số y = f(x) như sau:

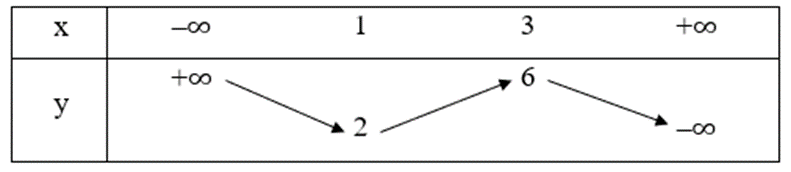
So sánh f(– 2021) và f(– 1); \(f\left( {\sqrt 3 } \right)\) và f(2).

Cho hàm số y = f(x) = – 3x.

a) Vẽ đồ thị hàm số y = – 3x.

b) So sánh f(–2) và f(5).

Tìm m để hàm số y = \(\sqrt {{x^2} + 4{\rm{x}} + m} \)có tập xác định là ℝ.

Cho DABC đều cạnh a. Gọi I là trung điểm BC.

a) Tính \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|\).

b) Tính \(\left| {\overrightarrow {BA} - \overrightarrow {BI} } \right|\).

Tìm giá trị thực của tham số m khác 0 để hàm số y = mx² – 2mx – 3m – 2 có giá trị nhỏ nhất bằng – 10 trên ℝ.

Cho tam giác ABC. Dựng phía ngoài tam giác các tam giác đều ABC', BCA', CAB'. Gọi M, N, P lần lượt là trung điểm của CA’, AB’, AC’. Chứng minh rằng:

a) MN = PC.

b) Gọi O là giao điểm của MN và PC. Chứng minh \(\widehat {MOC} = 60^\circ \).

Tìm đa thức M biết (x³ – 5x² + x – 5) = (x – 5).M

Rút gọn biểu thức sau

a) \(\sqrt {5 - 2\sqrt 6 } + \sqrt 2 \);

b) \(\sqrt {8 - 2\sqrt {15} } - \sqrt 5 \);

c) \(\sqrt {7 - 4\sqrt 3 } + 2\);

e) \(\sqrt {35 - 12\sqrt 6 } \);

g) \(\sqrt {7 - 3\sqrt 5 } \);

f) \(\sqrt {11 - 6\sqrt 2 } \).

Cho a, b, c > 0. Chứng minh \(\frac{{ab}}{c} + \frac{{bc}}{a} + \frac{{ca}}{b} \ge a + b + c\).

Cho tam giác ABC có a = 8, b = 10, \(\widehat C = 60^\circ \). Độ dài cạnh c là

Cho các điểm A(1; – 2), B(– 2;3) và C(0;4). Diện tích tam giác ABC bằng bao nhiêu?

Cho tập hợp A = (– ∞; 2023), B = [4 – 3m; + ∞). Tìm m để C_RB ⊂ A

Cho tứ giác ABCD. Gọi M, N, P lần lượt là trung điểm của AD, BC và AC. Biết MP = PN. Chọn câu đúng.

Trong lớp 10C có 45 học sinh trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Sử, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên.

Cho số phức z thỏa mãn \(\left| z \right|\) + z = 3 + 4i. Mô đun của z bằng?

Đồ thị hàm số y = ax³ + bx² + cx + d có hai điểm cực trị là A(1; – 7) và B (2; – 8). Tính y(– 1)

Tính hợp lí

1/ (– 37) + 14 + 26 + 37;

2/ (– 24) + 6 + 10 + 24;

3/ 15 + 23 + (– 25) + ( – 23);

4/ 60 + 33 + (– 50) + (– 33);

5/ (– 16) + ( – 209) + ( – 14) + 209;

6/ (– 12) + ( – 13) + 36 + (– 11);

7/ 300 – (– 200) – (– 120) + 18;

8/ – (– 299) + (– 219) – 401 + 12;

9/ 555 – (– 333) – 100 – 80;

10/ 34 + 35 + 36 + 37 – 14 – 15 – 16 – 17;

11/ 1+ (– 2) + 3 + (– 4) + ..... + 19 + (– 20);

12/ 1 – 2 + 3 – 4 + ... + 99 – 100.

Tìm điểm thuộc đồ thị y = – x + 2 có hoành độ gấp 3 lần tung độ.

Cho a và b là hai số dương khác nhau thỏa mãn \(a - b = \sqrt {1 - {b^2}} - \sqrt {1 - {a^2}} \).

Chứng minh a² + b² = 1.

Cho A(–1;2); B(2;0); C(3;4).

a) Tính tọa độ trung điểm I của AC.

b) Tính tọa độ trọng tâm G của tam giác ABC.

c) Tính tọa độ D: ABCD theo thứ tự là hình bình hành.

d) Tìm tọa độ E sao cho: \(3\overrightarrow {E{\rm{A}}} + 2\overrightarrow {EB} - \overrightarrow {EC} = \overrightarrow 0 \).

Cho đường tròn (O; R) và điểm A bên ngoài đường tròn. Từ A vẽ tiếp tuyến AB (B là tiếp điểm) và cát tuyến AMN đến (O). Trong các kết luận sau kết luận nào đúng:

Cho tam giác ABC có AB = AC, gọi D là trung điểm của BC. Chứng minh

a) Tam giác ADB bằng tam giác ADC.

b) AD là tia phân giác của góc BAC.

c) AD vuông góc BC.

Cho tam giác ABC có trọng tâm G, hai điểm M, N thỏa mãn \(\overrightarrow {MA} = 2\overrightarrow {MB} ;\)\(3\overrightarrow {NA} + 2\overrightarrow {NC} = \overrightarrow 0 \).

a) Xác định 2 điểm M,N.

b) Tính \(\overrightarrow {MN} \) theo 2 vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} \).

c) Tính \(\overrightarrow {MG} \)theo 2 vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} \). Suy ra 3 điểm M,N,G thẳng hàng.

Cho tam giác đều cạnh a, trọng tâm G . Tính\(\left| {\overrightarrow {GB} + \overrightarrow {GC} } \right|\).

Cho x, y >0; x + y ≤1. Tìm GTNN của \(M = xy + \frac{9}{{xy}}\).

Trên trục x'Ox cho 4 điểm A, B, C, D tùy ý. Để chứng minh \(\overline {AB} .\overline {C{\rm{D}}} + \overline {AC} .\overline {DB} + \overline {A{\rm{D}}} .\overline {BC} = 0\), một học sinh giải như sau:

Bước 1: Gọi a, b, c, d lần lượt là tọa đọ của điểm A, B, C, D trên trục x’Ox. Ta có

\(\overline {AB} .\overline {C{\rm{D}}} \) = (b – a)(d – c) = bd – ad – bc + ac                (1)

Bước 2: Tương tự \(\overline {AC} .\overline {{\rm{DB}}} \) = cb – ab – cd + ad            (2)

Bước 3: Tương tự \(\overline {AD} .\overline {BC} \) = dc – ac – ba + ab              (3)

Bước 4: Cộng (1), (2), (3) theo từng vế và rút gọn ta suy ra:

\(\overline {AB} .\overline {C{\rm{D}}} + \overline {AC} .\overline {DB} + \overline {A{\rm{D}}} .\overline {BC} = 0\)

Học sinh giải sai từ bước nào?

Tìm x biết

a) (x² – x + 7) ⋮ (x – 1);

b) (x² – 9x + 7) ⋮ (x – 9).

Xác định hàm số bậc nhất y = ax + b biết đồ thị hàm số của nó song song với đường thẳng y = 2x – 3 và cắt trục tung tại điểm có tung độ là 5.

Có 10 người, để làm xong một công việc thì phải mất 8 ngày. Nếu muốn làm xong công việc đó trong 5 ngày thì cần phải có bao nhiêu người, biết năng suất lao động của mỗi người là như nhau?

Cho 2 đường thẳng \[\left( {{d_1}} \right):y = \frac{1}{2}x + 2\] và (d₂): y = − x + 2. Gọi A, B lần lượt là giao điểm của (d₁) và (d₂) với trục Ox, C là giao điểm của (d₁) và (d₂). Tính chu vi và diện tích tam giác ABC.

Cho biểu thức \(P = \left( {\frac{{2 + x}}{{2 - x}} - \frac{{4{{\rm{x}}^2}}}{{{x^2} - 4}} - \frac{{2 - x}}{{2 + x}}} \right):\frac{{{x^2} - 3{\rm{x}}}}{{2{{\rm{x}}^2} - {x^3}}}\).a) Rút gọn P.b) Tìm giá trị nguyên của x để P chia hết cho 4.

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là các điểm nằm trên các cạnh BC, SC, SD, AD sao cho MN // BS, NP // CD, MQ // CD. Hỏi PQ song song với mặt phẳng nào sau đây?

Cho hình chóp S.ABCD, đáy là hình bình hành ABCD. Gọi M, N lần lượt là trung điểm SA, CD. Chứng minh MN // (SBC). 

Cho hình vuông ABCD cạnh a. Tính \(\left| {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {A{\rm{D}}} } \right|\).

Cho tam giác ABC, có bao nhiêu điểm M thỏa mãn \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = 3\)?

Cho tam giác đều ABC cạnh a, gọi G là trọng tâm. Khi đó giá trị \(\left| {\overrightarrow {AB} - \overrightarrow {GC} } \right|\) là:

Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB, cắt tiếp tuyến tại A của đường tròn ở điểm C. Chứng minh rằng CB là tiếp tuyến của đường tròn.

Cho hàm số bậc nhất y = (m – 2)x + m + 1 (m là tham số)

a) Với giá trị nào của m thì hàm số y là hàm số đồng biến?

b) Tìm giá trị của m để đồ thị hàm số đi qua điểm M(2; 6).

c) Đồ thị hàm số cắt trục hoành tại A, cắt trục tung tại B (A và B không trùng với gốc tọa độ O). Gọi H là chân đường cao hạ từ O của tam giác OAB. Xác định giá trị của m, biết \(OH = \sqrt 2 \).

Cho A =(– ∞; m],B= [3–2m; + ∞). Tìm m để

a) A giao B bằng rỗng, A giao B khác rỗng, A hợp B bằng ℝ.

b) A giaoB là 1 tập hợp có 1 phần tử.

Cho A = (m; m + 1) ; B = (3; 5)

a) Tìm m để A hợp B là một khoảng. Xác định các khoảng đó.

b) A ∩ B ≠ ∅.

c) A ∩ B = ∅.

Cho tam giác ABC. Xác định I sao cho \(3\overrightarrow {IA} - 2\overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \).

Trong mặt phẳng Oxy cho A(4;3), B(–1;2),C(3; –2),D(–2;m). Tìm tọa độ điểm I thỏa mãn \(\overrightarrow {IA} + 2\overrightarrow {IB} - \overrightarrow {IC} = \overrightarrow 0 \).