5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 29)

Cho hàm số f(x) có đạo hàm f’(x) = x(x − 1)(x + 4)³ , ∀ x ∈ R. Số điểm cực tiểu của hàm số đã cho là

Cho hàm số f(x) có đạo hàm f’(x) = x(x − 1)² , ∀ x ∈ R. Số điểm cực tiểu của hàm số đã cho là

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SD = \(\frac{3}{2}a\). Hình chiếu vuông góc của S lên mặt đáy (ABCD) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp S.ABCD và khoảng cách từ A đến mặt phẳng (SBD).

Cho hình vuông ABCD tâm O, trên đoạn BC lấy điểm E bất kì, trên tia đối của tia CD lấy điểm F sao cho CE = CF.

a) Chứng minh DE = BF.

b) Tia DE cắt BF tại H. Chứng minh \(\widehat {DHF}\) = 90°

c) Gọi I là trung điểm của EF, K là giao điểm của FE và BD. Chứng minh tứ giác AOIK là hình bình hành.

d) Chứng minh A, H, K thẳng hàng.

Cho hình vuông ABCD, gọi O là tâm của hình vuông. Một đường thẳng qua O cắt AD tại P, cắt BC tại Q.

a) Chứng minh AP = CQ

b) Kẻ Px vuông góc AC tại  E (E thuộc AC). Kẻ Qy vuông góc BD tại F (F thuộc BD), Px và Qy cắt nhau tại M. Chứng minh OEMF là hình chữ nhật.

c) Chứng minh M thuộc cạnh AB

d) Lấy K thuộc BC sao cho CK=DP. Chứng minh \(\widehat {MOK} = 90^\circ \).

Cho hình vuông ABCD . Gọi M, N lần lượt là trung điểm BC, CD. Chứng minh AN⊥DM.

Cho nửa đường tròn (O) đường kính AD. Trên nửa đường tròn lấy hai điểm B và C, biết AB = BC = \(2\sqrt 5 \) cm, CD = 6 cm. Tìm bán kính đường tròn.

Cho tam giác ABC có AB = 2, BC = 4, CA = 3.

a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} \), rồi suy ra cosA

b) Gọi G là trọng tâm của △ABC. Tính \(\overrightarrow {AG} .\overrightarrow {BC} \)

c) Tính giá trị biểu thức S = \(\overrightarrow {GA} .\overrightarrow {GB} + \overrightarrow {GB} .\overrightarrow {GC} + \overrightarrow {GC} .\overrightarrow {GA} \)

d) Gọi AD là phân giác trong của góc BAC (D ∈ BC). Tính \(\overrightarrow {A{\rm{D}}} \) theo \(\overrightarrow {AB} ;\overrightarrow {AC} \)suy ra AD.

Gọi G là trọng tâm tam giác ABC và I, J thỏa mãn \(\overrightarrow {IA} = 2\overrightarrow {IB} ,3\overrightarrow {J{\rm{A}}} + 2\overrightarrow {JC} = \overrightarrow 0 \)

a) Phân tích \(\overrightarrow {{\rm{IJ}}} \) theo \(\overrightarrow {AB} ,\overrightarrow {AC} \)

b) Chứng minh rằng IJ qua G.

Cho tam giác ABC. Tìm tập hợp các điểm M trong mỗi trường hợp sau:

a) \(\overrightarrow {MA} = \overrightarrow {MB} \).

b) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \).

c) \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA} + \overrightarrow {MC} } \right|\).

Cho tam giác ABC. Tìm tập hợp các điểm M thỏa mãn \(\left| {\overrightarrow {MA} + \overrightarrow {MC} } \right| = \left| {\overrightarrow {MA} - \overrightarrow {MB} } \right|\).

Cho tam giác ABC. Tìm tập hợp các điểm M sao cho \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = \left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|\)

Cho tam giác ABC và ABD vuông có chung cạnh huyền AB ( C, D cùng thuộc 1 nua mp có bờ là AB).

a) Chứng minh A, B , C, D cùng thuộc 1 đường tròn và gọi đường tròn đó có tâm O

b) Chứng minh CD < AB.

c) Giả sử 2 đoạn thẳng CD cắt AB tại M. Chứng minh OM= \(\frac{{MA + MB}}{2}\).

Cho tam giác ABC. Gọi I là trung điểm của BC; D và E là hai điểm sao cho \(\overrightarrow {B{\rm{D}}} = \overrightarrow {DE} = \overrightarrow {EC} \)

a) Chứng minh: \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {A{\rm{D}}} + \overrightarrow {A{\rm{E}}} \)

b) Tính véctơ: \(\overrightarrow {AS} = \overrightarrow {AB} + \overrightarrow {A{\rm{D}}} + \overrightarrow {AC} + \overrightarrow {A{\rm{E}}} \) theo \(\overrightarrow {AI} \)

c) Suy ra ba điểm A, I, S thẳng hàng.

Cho tứ giác ABCD có AB = AD; CB = CD (ta gọi tứ ABCD trong trường hợp này là tứ giác có hình ảnh cánh diều)

a) Chứng minh AC là đường trung trực của BD

b) Tính góc B và góc D(biết\(\widehat A = 100^\circ ,\widehat C = 60^\circ \)).

Cho tam giác ABC và tam giác A’B’C’ có trọng tâm lần lượt là G và G’. Chứng minh rằng \[\overrightarrow {{\rm{AA'}}} + \overrightarrow {BB'} + \overrightarrow {CC'} = 3\overrightarrow {GG'} \]. Từ đó suy ra điều kiện cần và đủ để hai tam giác có cùng trọng tâm.

Cho hàm số f(x) có đạo hàm f’(x) = x(x – 1)(x + 2)³ ; ∀ x ∈ R. Số điểm cực trị của hàm số đã cho là:

Một thiết bị gồm có 3 bộ phận. Trong khoảng thời gian T, việc các bộ phận đó bị hỏng là độc lập với nhau và với các xác suất tương ứng là: 0,1; 0,2; 0,3. Cả thiết bị sẽ bị hỏng nếu có ít nhất một bộ phận hư hỏng. Tìm xác suất thiết bị hoạt động tốt trong thời gian T đó.

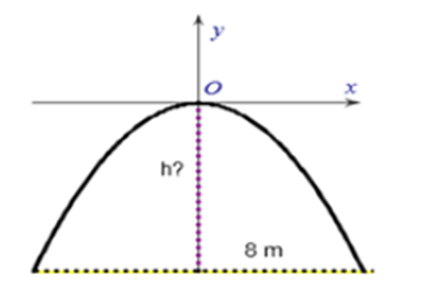
Một chiếc cổng hình parabol dạng y = \( - \frac{1}{2}{x^2}\)có chiều rộng d = 8m. Hãy tính chiều cao h của cổng (Xem hình minh họa bên cạnh)

Một ôtô đi trên quãng đường AB với v = 54 km/h. Nếu giảm vận tốc đi 9 km/h thì ôtô đến B trễ hơn dự định 45 phút. Tính quãng đường AB và thời gian dự tính để đi quãng đường đó.

Để tính diện tích tam giác cân, người Ai Cập cổ lấy nửa đáy nhân với cạnh bên. Nếu 1 tam giác cân có cạnh đáy bằng 4m, cạnh bên 10m thì sai số trong cách tính trên so với cách tính đúng là bao nhiêu phần trăm?

Trong cuộc thi “ Rung chuông vàng”, đội Thủ Đức có 20 bạn lọt vào vòng chung kết, trong đó có 5 bạn nữ và 15 bạn nam. Để sắp xếp vị trí chơi, ban tổ chức chia các bạn thành 4 nhóm A, B, C, D, mỗi nhóm có 5 bạn. Việc chia nhóm được thực hiện bằng cách bốc thăm ngẫu nhiên. Tính xác suất để 5 bạn nữ thuộc cùng một nhóm gần nhất với:

Trong khai triển (1 + ax)ⁿ ta có số hạng đầu là 1, số hạng thứ hai là 24x, số hạng thứ ba là 252x² . Hãy tìm a và n.

Tìm m để các hàm số sau có tập xác định là R (hay luôn xác định trên R):

a) y = f(x) = \(\frac{{3x + 1}}{{{x^2} + 2(m - 1)x + {m^2} + 3m + 5}}\)

b) y = f(x) = \(\sqrt {{x^2} + 2\left( {m - 1} \right)x + {m^2} + m - 6} \)

c) y = f(x) = \(\frac{{3x + 5}}{{{x^2} - 2(m + 3)x + m + 9}}\)

Cho tứ giác ABCD. Tìm điểm O sao cho \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {O{\rm{D}}} = \overrightarrow 0 \)

Cho đoạn thẳng AB có trung điểm I. M là điểm tùy ý không nằm trên đường thẳng AB. Trên MI kéo dài, lấy một điểm N sao cho IN = MI.

a) Chứng minh: \(\overrightarrow {BN} - \overrightarrow {BA} = \overrightarrow {MB} \)

b) Tìm các điểm D, C sao cho \(\overrightarrow {NA} + \overrightarrow {NI} = \overrightarrow {N{\rm{D}}} ;\overrightarrow {NM} - \overrightarrow {BN} = \overrightarrow {NC} \).

Tìm x và y biết \(\frac{{x + 4}}{{7 + y}} = \frac{4}{7}\) và x + y = 22

Tìm x và y biết \(\frac{x}{{19}} = \frac{y}{{21}}\) và 2x – y = 34

Hàm số y =\(\frac{{{x^2} - 2{\rm{x}}}}{{x - 1}}\) đồng biến trên khoảng

Tỉ lệ phế phẩm của một nhà máy là 5%. Tìm xác xuất để trong 12 sản phẩm do nhà máy đó sản xuất ra có

a) 2 phế phẩm

b) không quá 2 phế phẩm.

Xác định đường thẳng đi qua A(4 ; 3), cắt trục tung tại điểm có tung độ là 1 số nguyên dương, cắt trục hoành tại 1 điểm có hoành độ là 1 số nguyên tố.

Tìm x, y biết x : y : z = 3 : 8 : 5 và 3x + y –  2z = 14.

Điền số thích hợp vào chỗ trống: 271 km 25m = ....m.

Tìm tập xác định của hàm số sau:

a) y=3x² – 2x +1

b) y= \(\frac{{3\left| x \right| + 2}}{{x - 2}}\)

c) y=\(\sqrt {x - 2} + \sqrt {3 - x} \)

d) y = \(\frac{{\frac{{2{\rm{x}} - 1}}{{\sqrt {4 - 3{\rm{x}}} }}}}{x}\)

e) y = \(\frac{{\sqrt {x + 3} }}{{2 - x}}\)

f) y = \(\frac{{2{\rm{x}} + 1}}{{{x^2} - 3{\rm{x}} + 2}}\)

g) y = \(\frac{{x - 1}}{{{x^2} - 1}} - 3x\)

Cho (O;R) đường kính AD, dây AB , qua B kẻ dây BC vuông góc AD tại H . Tính bán kính R của đường tròn biết AB = 10 cm, BC = 12 cm.

Cho tam giác ABC bất kì, gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. H, H' lần lượt là trực tâm của tam giá ABC, MNP. Điểm K đối xứng H qua H'. Khẳng định nào sau đây đúng?

Phân số cần những điều kiện gì để trở thành 1 số nguyên?

Hàm số nào trong các hàm sau đây không phải là hàm số bậc hai?

Một số nếu giảm xuống 3 lần rồi bớt đi 14,6 thì được kết quả là 30,4. Tìm số đó.

Giải phương trình: \({\left( {\sin \frac{x}{2} + cos\frac{x}{2}} \right)^2} + \sqrt 3 \cos x = 2\)

Cho tam giác ABC. Các điểm M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Chứng minh rằng với điểm O bất kì, ta có \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} \).

Tìm x, y, z biết \(\frac{{x - 1}}{2} = \frac{{y + 3}}{4} = \frac{{z - 5}}{6}\) và 5z – 3x – 4y = 50.

Cho 5 điểm A, B, C, D, E. Chứng minh rằng:

a) \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {E{\rm{A}}} = \overrightarrow {CB} + \overrightarrow {E{\rm{D}}} \).

b) \(\overrightarrow {AC} + \overrightarrow {CD} - \overrightarrow {EC} = \overrightarrow {A{\rm{E}}} - \overrightarrow {DB} + \overrightarrow {CB} \).

Cho 6 điểm A, B, C, D, E, F. Chứng minh rằng:

\(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EF} = \overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} \)