5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 2)

Hình thang với hai cạnh bên bằng nhau, góc tù bằng 120^o thì có phải là hình thang cân không ?

Hình thang có 2 cạnh bên bằng nhau có phải là hình thang cân không? Vì sao?

Cho hàm số y = x² và y = mx + 4, với m là tham số.

a) Khi m = 3, tìm tọa độ các giao điểm của hai đồ thị hàm số trên.

b) Chứng minh rằng với mọi giá trị m, đồ thị của hai hàm số đã cho luôn cắt nhau tại hai điểm phân biệt A₁(x₁,y₁); A₂ (x₁ ,y₂). Tìm tất cả các giá trị của m sao cho (y₁)² + (y₂)² = 7².

Cho hàm số bậc nhất y = mx - 4. Tìm m trong các trường hợp sau

a) Đồ thị cắt đường thẳng y = 2x - 1 tại điểm hoành độ bằng 2.

b) Đồ thị cắt đường y = -3x + 2 tạiđiểm có tung độ bằng 5.

Hai góc tương ứng là gì?

Cho tam giác ABC, lấy D là trung điểm của AC. Từ A vẽ đường thẳng song song với BC, cắt BD tại E. Tại cạnh BC lấy điểm M sao cho DM cắt AE tại N. Chứng minh rằng:

a) \[\widehat {AED} = \widehat {CBD}\]
b) \[\widehat {DNE} = \widehat {DMB}\]
c) \[\widehat {BAD} = \widehat {DCE}\].

Có bao nhiêu phân số thập phân có tử số là 3, lớn hơn \(\frac{1}{{34}}\) và nhỏ hơn \(\frac{1}{8}\).

Tìm x: \[9{\left( {x + 1} \right)^2} - \left( {3x - 2} \right)\left( {3x + 2} \right) = 10\]

Tú và Hiếu có 40 viên bi, sau khi Hiếu cho Tú 2 viên thì số bi của Hiếu bằng \(\frac{2}{3}\) số bi của Tú. Hỏi ban đầu Tú có bao nhiêu viên.

Xác định số đo góc nhỏ nhất của một tứ giác lồi, biết rằng số đo 4 góc lập thành một cấp số cộng và góc lớn nhất bằng 5 lần góc nhỏ nhất.

Xác định 4 góc của một tứ giác lồi, biết rằng đo 4 góc lập thành 1 cấp số cộng và góc lớn nhất bằng 5 lần góc nhỏ nhất ?

Hiện nay bố 32 tuổi, con 5 tuổi . Hỏi mấy năm nữa thì tuổi bố gấp 4 lần tuổi con?

Tìm số thực a biết: \[{x^4} - 6{x^3} + 12{x^2} - 14x + 3a\] chia x – 2 dư 3

Trong mặt phẳng Oxy cho đường thẳng 2x - y + 1 = 0. Để phép tịnh tiến theo vecto \(\overrightarrow v \)biến đường thẳng d thành chính nó thì \(\overrightarrow v \) phải là vecto nào trong các vecto sau?

36dm =.......m

Một tổ công nhân có 12 người. Cần chọn 3 người, một người làm tổ trưởng, một tổ phó và một thành viên. Hỏi có bao nhiêu cách chọn?

Cho lục giác ABCDEF. Có bao nhiêu vectơ khác vectơ – không có điểm đầu và điểm cuối là đỉnh của lục giác.

Cho tam giác ABC có trọng tâm G. Khi đó:

Cho tam giác ABC có trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm của các cạnh BC, CA, AB. Phép vị tự tâm G biến tam giác ABC thành tam giác A’B’C’ có tỉ số vị tự bằng bao nhiêu?

Tổng tất các nghiệm thuộc đoạn \[\left[ {0,10\pi } \right]\]của phương trình \[{\sin ^2}2x + \;3.\sin \;2x\; + \;2\; = \;0\]

Tính tổng T các nghiệm của phương trình sin2x – cosx = 0 trên \[\left[ {0;2\pi } \right].\]

Thực hiện các phép tính:

a. \[{3.5^2} - 16:{2^2}\]

b. \[{2^3}.17--{2^3}.14\]

c. \[15.141 + 59.15\]

d. \[17.85 + 15.17--120\]

e. \[20--\left[ {30--{{\left( {5--1} \right)}^2}} \right]\]

Từ một điểm A nằm bên ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC với đường tròn. Đường thẳng vuông góc với OB tại O cắt tia AC tại N. Đường thẳng vuông góc với OC tại O cắt AB tại M.

1. Xác định hình tính của tứ giác AMON.

2. Điểm A phải cách O một khoảng là bao nhiêu để MN là tiếp tuyến của (O)?

Cho hình bình hành ABCD có AB = 2AD. Gọi E, F thứ tự là trung điểm của AB và CD

a) Các tứ giác AEFD, AECF là hình gì? Vì sao?

b) Gọi M là giao điểm của AF và DE, gọi N là giao điểm của BF và CE. Chứng minh rằng tứ giác EMFN là hình chữ nhật.

Tam giác ABC có hai đường trung tuyến BM, CN vuông góc với nhau và có BC = 3, góc \[\widehat {BAC} = {30^0}\]. Tính diện tích tam giác ABC.

Chứng minh rằng: nếu 1 tam giác có 2 đường trung tuyến vuông góc với nhau thì tổng các bình phương của 2 đường trung tuyến này bằng bình phương của đường trung tuyến thứ ba.

Tam giác ABC có hai trung tuyến AM và BN vuông góc với nhau. Hãy tính diện tích tam giác đó theo AM và BN

Tìm ảnh của đường tròn (C) qua phép quay tâm O, góc quay -90° biết: (C): (x + 4)² + (y - 1)² = 16

Tìm ảnh của đg tròn (C) : \({(x - 1)^2} + {(y + 2)^2} = 9\)qua phép quay Q( I; 90°) với I(3; 4)

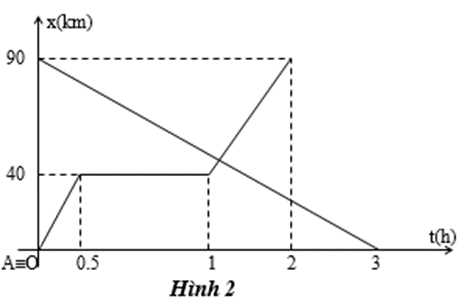
Cho đồ thị chuyển động của hai xe được mô tả trên hình vẽ.

a. Hãy nêu đặc điểm chuyển động của hai xe.

b. Tình thời điểm hai xe gặp nhau, lúc đó mỗi xe đi được quãng đường là bao nhiêu ?(Hình 2)

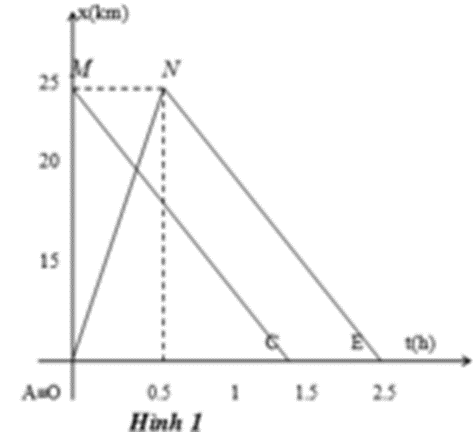
Cho đồ thị chuyển động của hai xe được mô tả như hình vẽ. (Hình 1). Hãy nêu đặc điểm chuyển động của mỗi xe và viết phương trình chuyển động

Cho a, b, c > 0 và a + b + c = 1. tìm GTLN của \[\frac{a}{{a + 1}} + \frac{b}{{b + 1}} + \frac{c}{{c + 1}}\]

Tính giá trị nhỏ nhất của \(A = \frac{1}{a} + \frac{1}{b} + \frac{1}{c}\)với a, b, c > 0 và \(a + b + c = 3abc\)

Xét các mệnh đề sau

(I): Véc tơ – không là véc tơ có độ dài bằng 0.

(II): Véc tơ – không là véc tơ có nhiều phương.

Tính tổng các số lẻ liên tiếp từ 1 đến 99

Tổng các số tự nhiên từ 1 đến 99 là:

Tổng các ước tự nhiên của số 75 là?

Số ước tự nhiên của 75 là bao nhiêu?

Cho a, b N. Chứng tỏ rằng nếu 5a + 3b và 13a + 8b cùng chia hết cho 2012 thì a và b cũng chia hết cho 2012

Số nào sau đây: 13, 15, 17, 19 là hợp số?

Cho tam giác ABC vuông tại A có AB = 3cm; AC = 4cm, đường cao AH.
a) Tính BC,AH;
b) Vẽ (A:AH), vẽ HI vuông góc với AC, HI cắt (A) tại M. Chứng minh: CM là tiếp tuyến của (A);
c) Vẽ đường kính MG của (A). Chứng minh BG là tiếp tuyến của (A)

Có bao nhiêu số tự nhiên lẻ có 4 chữ số khác nhau?

Có bao nhiêu số tự nhiên có bốn chữ số đôi một khác nhau?

Tìm số hạng thứ 7 trong khai triển \({(x + 2)^{10}}\)

Tìm số hạng thứ năm trong khai triển \[{\left( {x\; + \;\frac{2}{x}} \right)^{10}}\] mà trong khai triển đó số mũ của x giảm dần.

Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh lớp 12A, 3 học sinh lớp 12B và 5 học sinh lớp 12C thành một hàng ngang. Xác suất để trong 10 học sinh trên không có 2 học sinh cùng lớp đứng cạnh nhau bằng

Một nhóm gồm 10 học sinh trong đó có 4 nữ và 6 nam. Hỏi có bao nhiêu cách xếp 10 học sinh trên thành 1 hàng dọc sao cho 4 học sinh nữ phải đứng liền nhau?

Có 6 học sinh nam và 2 học sinh nữ được xếp thành một hàng ngang. Hỏi có bao nhiêu cách xếp sao cho hai học sinh nữ không đứng cạnh nhau?

Một cái bể bơm có thể bơm đầy 1 cái bể trong 6 giờ . máy thứ hai bơm đầy bể mất \(\frac{2}{3}\) số giờ đó , máy thứ ba bơm đầy bể mất \(\frac{1}{2}\) số giờ mà máy thứ hai bơm đầy bể. Hỏi nếu mở đồng loạt cả ba máy cùng 1 múc thì bao lâu bể đầy.

Hai máy bơm cùng làm việc thì sau 12 giờ bơm nước đầy bể, nếu máy bơm thứ nhất làm 3 giờ và máy bơm thứ hai làm 18 giờ thì hai máy cũng bơm nước đầy bể. hỏi nếu làm một mình thì mỗi máy bơm đầy bể trong bao lâu?

Cho đường thẳng d \[y = \left( {2m + 1} \right).x - 2\]và m khác \(\frac{1}{2}\)giả sử d cắt ox tại a cắt oy tại b. Tìm m để diện tích tam giác OABbằng \(\frac{1}{2}\)

Cho \({2^n} + 1\) là số nguyên tố (n > 2)

Chứng minh \({2^n} - 1\) là hợp số

Cho \({2^n} - 1\) là số nguyên tố. Chứng minh n cũng là số nguyên tố.

Số 0 và số 1 có phải số chính phương không?

Tứ giác ABCD có \[\widehat A:\widehat B:\widehat C:\widehat D\]tỉ lệ với 3 : 4 : 5 : 6
a) Tính các góc của tứ giác
b) Tứ giác ABCD là hình gì ? Vì sao?

Cho tứ giác ABCD biết số đo của các góc \[\widehat A;\;\widehat B;\widehat C;\widehat D\] tỉ lệ thuận với 4 : 3 : 5 : 6. Khi đó số đo các góc\[\widehat A;\;\widehat B;\widehat C;\widehat D\]  lần lượt là:

Anh Long đi taxi từ nhà đến ga tàu hết 35.000 đồng, biết rằng đoạn đường từ nhà anh long đến ga là 2,5 km. Hỏi trung bình đi mỗi km bằng taxi anh Long phải trả bao nhiêu tiền ?

Cho hình bình hành ABCD. Chứng minh rằng với mọi điểm M, ta có:\[\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \]

Chứng minh với mọi x thuộc N, \({x^2} + 1\)không chia hết cho 3.

Tổng 2 số lẻ là 884. Tìm 2 số, biết rằng giữa chúng có 7 số chẵn liên tiếp nữa?

Tìm hai số lẻ biết tổng của chúng là 50 và giữa chúng có ba số lẻ khác.

Cho nửa đường tròn (O) đường kính AB = 2R. Vẽ đường thẳng d là tiếp tuyến của (O) tại B. Trên cung AB lấy điểm M tùy ý tia AM cắt d tại N. Gọi C là trung điểm của AM tia CO cắt d tại D.

a ) CMR OBNC nội tiếp.

b ) CMR NO vuông góc với AD.

c ) CMR CA . CN = CO . CD

d ) Xác định vị trí điểm M để (2AM + AN ) đạt GTNN.

Cho đường tròn tâm O bán kính R và một đường thẳng d cố định không giao nhau. Hạ OH vuông góc với d. M là một điểm tùy ý trên d (M không trùng với H). Từ M kẻ hai tiếp tuyến MP và MQ với đường tròn (O; R) (P, Q là các tiếp điểm và tia MQ nằm giữa hai tia MH và MO). Dây cung PQ cắt OH và OM lần lượt tại I và K.

1) Chứng minh rằng tứ giác OMHQ nội tiếp.

2) Chứng minh rằng \[\widehat {OMH} = \widehat {OIP}\]

3) Chứng minh rằng khi M di chuyển trên đường thẳng d thì điểm I luôn cố định.

4) Biết \[OH = R\sqrt 2 \], tính IP . IQ.

Một vật hình hộp chữ nhật có kích thước 30 . 20 . 10 (cm)

Ta thả ''nằm'' vật vào bình trụ đựng nước

a) Thể tích phần chòm của vật là bao nhiêu? Chiều cao phần vật chìm trong nước là mấy ?

b) Nếu ta đổ dầu vào cho vật ngập hoàn toàn thì thể tích vật ngập trong nước có thay đổi không ?

c) Lượng dầu đổ vào tối thiểu là mấy biết diện tích đáy bình trụ là 20dm^{2 .} cho biết trọng lượng riêng nước, dầu, vật lần lượt là 10000N/m³; 8000N/m³; 9000N/m³ ?

Một hình hộp chữ nhật có chiều dài 20 cm, chiều rộng 15 cm, chiều cao 10 cm. Bạn Bình dán giấy màu đỏ vào các mặt xung quanh và giấy màu vàng vào hai mặt bên cái hộp đó chỉ dán mặt ngoài. Hỏi diện tích tích giấy màu nào lớn hơn và lớn hơn bao nhiêu cm²?

Tìm số nguyên tố p sao cho p + 8 và p + 16  đều là các số nguyên tố.

Cho tam giác ABC có M là trung điểm của BC, I là trung điểm của AM. Khẳng định nào sau đây đúng?

Cho tam giác ABC có M là trung điểm của BC, I là trung điểm của AM. Khẳng định nào sau đây đúng ?

Chứng minh đẳng thức sau :

\[\frac{{1 + si{n^2}x}}{{1 - si{n^2}x}} = 1 + 2ta{n^2}x\]

Cho hình bình hành ABCD có tâm O. M là một điểm bất kì trong mặt phảng.CMR:

a) \[\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{ OD}}} {\rm{ + }}\overrightarrow {{\rm{OC}}} = \overrightarrow {AC} \]

b) \[\overrightarrow {{\rm{BA}}} {\rm{ + }}\overrightarrow {{\rm{BC}}} {\rm{ + }}\overrightarrow {{\rm{OB}}} = \overrightarrow {OD} \]

c) \[\overrightarrow {{\rm{BA}}} {\rm{ + }}\overrightarrow {{\rm{BC}}} {\rm{ + }}\overrightarrow {{\rm{ OB}}} = \overrightarrow {MO} - \overrightarrow {MB} \]

Biết chu vi của một hình chữ nhật gấp 6 lần chiều rộng. Hỏi chiều dài gấp mấy lần chiều rộng?

Cho hình thang cân abcd (ab // cd) có 2 đường chéo vuông góc. Biết đường cao AH = a. Hãy tính tổng 2 đáy theo a

Chứng minh các đẳng thức sau:

a) (a - b) + (c - d) - (a + c) = - (b + d)

b) (a - b) - (c - d) + (b + c) = a + d

Cho tứ giác ABCD chứng minh

a) AB < BC + CD + AD

b) AC + BD < AB + BC + CD + AD

Tìm GTNN của biểu thức sau: 5x² - 6x + 9

Hàm số \[{\rm{y = 5}}{{\rm{x}}^{\rm{2}}}{\rm{ - 4x + 6}}\] có giá trị nhỏ nhất khi:

Cho hbh ABCD. Gọi M và N là trung điểm của AB và CD. AN và CM cắt BD tại E và F.

Chứng minh \[\overrightarrow {DE} \, = \overrightarrow {EF} \;\, = \overrightarrow {FB} \]

Cho hình bình hành ABCD. Gọi M là trung điểm cạnh BC. Hãy biểu thị \[\overrightarrow {{\rm{AM}}} \] theo \[\overrightarrow {{\rm{AB}}} \] và \[\overrightarrow {{\rm{AD}}} {\rm{.}}\]

Cho \[\Delta ABC\]vuông tại A. Gọi M là trung điểm của BC. Từ M hạ MP vuông góc với AB, \[{\rm{P }} \in {\rm{ AB}}\], \(MQ \bot AC\left( {Q \in AC} \right)\) R đối xứng M qua P

a, AQMP là hình gì ? Vì sao?

b, AMBR là hình gì ? Vì sao?

c, Điều kiện để tâm giác ANG để AQM P là hình vuông

Cho \[\Delta ABC\]đều, đường cao AH. Lấy M nằm giữa B, C. Kẻ \[{\rm{MP }} \bot {\rm{ AB}}\]tại P ; \[{\rm{MQ }} \bot {\rm{AC}}\] tại Q. Gọi O là trung điểm AM. Chứng minh OHPQ là hình thoi. Tìm vị trí của M trên BC để PQ ngắn nhất.

Cho các số thực dương x, y, z thỏa x² + y² + z² = 3xyz. Chứng minh:

\[\frac{{{{\rm{x}}^{\rm{2}}}}}{{{{\rm{x}}^{\rm{4}}}{\rm{ + yz}}}}{\rm{ + }}\frac{{{{\rm{y}}^{\rm{2}}}}}{{{{\rm{y}}^{\rm{4}}}{\rm{ + xz}}}}{\rm{ + }}\frac{{{{\rm{z}}^{\rm{2}}}}}{{{{\rm{z}}^{\rm{4}}}{\rm{ + xy}}}} \le \frac{{\rm{3}}}{{\rm{2}}}\]

Cho các số thực dương x, y, z thỏa mãn \[{{\rm{x}}^{\rm{2}}}{\rm{ + }}{{\rm{y}}^{\rm{2}}}{\rm{ + }}{{\rm{z}}^{\rm{2}}}{\rm{ = 3xyz}}{\rm{.}}\]

Tìm giá trị lớn nhất của biểu thức: \[{\rm{P = }}\frac{{{{\rm{x}}^{\rm{2}}}}}{{{{\rm{x}}^{\rm{4}}}{\rm{ + yz}}}}{\rm{ + }}\frac{{{{\rm{y}}^{\rm{2}}}}}{{{{\rm{y}}^{\rm{4}}}{\rm{ + xz}}}}{\rm{ + }}\frac{{{{\rm{z}}^{\rm{2}}}}}{{{{\rm{z}}^{\rm{4}}}{\rm{ + xy}}}}{\rm{.}}\]

Khi nhân một số với 39, một học sinh đã đặt nhầm các tích riêng thẳng cột nên tìm ra kết quả là 259,2. Tìm tích đúng.

Một cửa hàng nhập về 50 chiếc túi xách với giá góc 150 000 đồng/cái. Cửa hàng đã bán 30 chiếc với giá mỗi chiếc lãi 30% so với giá gốc, 20 chiếc còn lại bán lỗ 5% so với giá gốc. Hỏi sau khi bán hết 50 chiếc túi xách cửa hàng đó lãi hay lỗ bao nhiêu tiền?

Rút gọn BT:

\[{\rm{A = si}}{{\rm{n}}^{\rm{2}}}{\rm{2}}{{\rm{1}}^{\rm{o}}}{\rm{ + co}}{{\rm{s}}^{\rm{2}}}{\rm{2}}{{\rm{1}}^{\rm{o}}}{\rm{ + tan1}}{{\rm{8}}^{\rm{o}}}{\rm{ - cot7}}{{\rm{2}}^{\rm{o}}}\]

Rút gọn:

a) \[{\rm{si}}{{\rm{n}}^{\rm{2}}}\left( {{\rm{54}}} \right){\rm{ + }}\frac{{{\rm{5cot}}\left( {{\rm{72}}} \right)}}{{{\rm{4tan}}\left( {\rm{8}} \right)}}{\rm{ + si}}{{\rm{n}}^{\rm{2}}}\left( {{\rm{36}}} \right){\rm{ + sin}}\left( {{\rm{30}}} \right)\]

b) \[{\rm{ta}}{{\rm{n}}^{\rm{2}}}{\rm{\alpha }}\left( {{\rm{2co}}{{\rm{s}}^{\rm{2}}}{\rm{\alpha   + si}}{{\rm{n}}^{\rm{2}}}{\rm{\alpha   - 1}}} \right)\]

Tìm tất cả các giá trị của x để P < 1.

Có\[{\rm{P = }}\frac{{\rm{x}}}{{\sqrt {\rm{x}} {\rm{ - 1}}}}\]. Tìm giá trị nguyên của x để \[{\rm{P\;}} \le {\rm{ 4}}\]

Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau: \[y = \frac{1}{2}x\](d₁) và \[{\rm{y = }}\frac{1}{2}{\rm{x + 3}}\](d₂). Xác định b để đường thẳng (d₃) y = 2x + b cắt (d₂) tại điểm có tung độ và hoành độ đối nhau.

Xác định phương trình parabol (P) \({\rm{y = a}}{{\rm{x}}^{\rm{2}}}\)để (P) tiếp xúc với đường thẳng (d) y = - 4x + 4

Tìm tham số m để đường thẳng d:\[{\rm{y = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{x + m}}\] tiếp xúc với parabol (P): \[{\rm{y = }}\frac{{{{\rm{x}}^{\rm{2}}}}}{{\rm{2}}}\]

Vẽ đồ thị hàm số y = 2x.
Đồ thị hàm số không đi qua điểm nào trong các điểm sau:

Điểm thuộc đồ thị hàm số y = −2x là :

Chứng minh các đẳng thức sau với \[{\rm{n\;}} \in {{\rm{N}}^{\rm{*}}}\]\[{{\rm{A}}_{\rm{n}}}{\rm{\; = \;}}\frac{{\rm{1}}}{{{\rm{1}}{\rm{.2}}{\rm{.3}}}}{\rm{\; + \;}}\frac{{\rm{1}}}{{{\rm{2}}{\rm{.3}}{\rm{.4}}}}{\rm{\; + \;}}...{\rm{\; + \; }}\frac{{\rm{1}}}{{{\rm{n}}\left( {{\rm{n + 1}}} \right)\left( {{\rm{n + 2}}} \right)}}{\rm{\; = \;}}\frac{{{\rm{n}}\left( {{\rm{n + 3}}} \right)}}{{{\rm{4}}\left( {{\rm{n + 1}}} \right)\left( {{\rm{n + 2}}} \right)}}\]

Tính tổng :

\[{{\rm{S}}_{\rm{n}}}{\rm{ = }}\frac{{\rm{1}}}{{{\rm{1}}{\rm{.2}}{\rm{.3}}}}{\rm{ + }}\frac{{\rm{1}}}{{{\rm{2}}{\rm{.3}}{\rm{.4}}}}{\rm{ + }}\frac{{\rm{1}}}{{{\rm{3}}{\rm{.4}}{\rm{.5}}}}{\rm{ + }}...{\rm{ + }}\frac{{\rm{1}}}{{{\rm{n}}\left( {{\rm{n + 1}}} \right)\left( {{\rm{n + 2}}} \right)}}\]

Chứng mình rằng: \[{{\rm{(a + b)}}^{\rm{2}}}{\rm{ - (a - b}}{{\rm{)}}^{\rm{2}}}{\rm{ = 4ab}}\]

Chứng minh các bất đẳng thức sau 3n − 1 > n(n + 2) với \[{\rm{n }} \ge {\rm{ 4}}\]

Chứng minh rằng với mọi số tự nhiên \[{\rm{n\;}} \ge {\rm{2}}\], ta có bất đẳng thức: 3ⁿ > 3n + 1

Cho tam giác MNP, gọi K là điểm thuộc đoạn thẳng NP sao cho \[{\rm{NK = }}\frac{1}{4}{\rm{NP}}\]và I là trung điểm của đoạn thẳng MK. Mệnh đề nào dưới đây đúng?