5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 18)

Cho hai đường thẳng \(\left( {{D_1}} \right):y = \frac{1}{2}x + 2\) và \(\left( {{D_2}} \right):y = - x + 2\)

Gọi A và B theo thứ tự giao điểm của (D₁) và (D₂) với các trục hoành, C là giao điểm của hai đường thẳng đó (đơn vị trên các trục tọa độ là centimet).

Khẳng định nào sau đây sai?

Chứng minh: \(S = 1 + \frac{1}{2} + \frac{1}{3} + \cdot \cdot \cdot + \frac{1}{{63}} + \frac{1}{{64}} > 4\).

Tìm m để hàm số \(y = \frac{{\sqrt {x - 2m + 3} }}{{x - m}} + \frac{{3x - 1}}{{\sqrt { - x + m + 5} }}\) xác định trên khoảng (0; 1)?

Tìm tất cả các giá trị thực của tham số m để hàm số

\(y = \sqrt {x - m + 1} + \frac{{2x}}{{\sqrt { - x + 2m} }}\) xác định trên khoảng (−1; 3).

Tìm x biết x³ − 3x + 2 = 0.

Cho hình bình hành ABCD, gọi O là giao điểm của AC và BD. Các khẳng định sau đúng hay sai?

a) \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right|;\)

b) \(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {CB} ;\)

c) \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD} .\)

Cho hình bình hành ABCD. Gọi O là giao điểm 2 đường chéo AC và BD. Qua O vẽ đường thẳng a cắt AD, BC lần lượt tại E, F. Qua O vẽ đường thẳng b cắt AB và CD lần lượt tại K, H. Chứng minh tứ giác EKFH là hình bình hành.

Cho hai tập hợp \(E = \left( {2;\;5} \right]\) và \(F = \left[ {2m - 3;\;2m + 2} \right]\). Tìm tất cả các giá trị của tham số m để E hợp F là một đoạn có độ dài bằng 5.

Tìm m để đa thức: A(x) = x³ − 3x² + 5x +m chia hết cho đa thức B(x) = x − 2

Tính độ dài MN trên hình vẽ.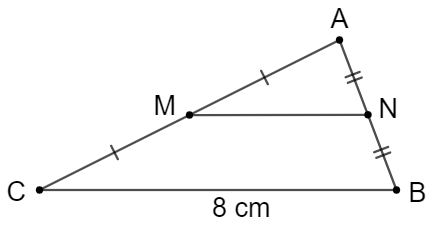

Cho hình bình hành ABCD. Gọi O là giao điểm 2 đường chéo AC và BD. Đường thẳng qua O không song song với AD cắt AB tại M và CD tại N.

a) Chứng minh M đối xứng với N qua O.

b) Chứng tỏ rằng tứ giác AMCN là hình bình hành.

Cho hình bình hành ABCD. Gọi O là giao điểm 2 đường chéo AC và BD. Qua O vẽ đường thẳng a cắt AD, BC lần lượt tại E, F. Qua O vẽ đường thẳng b cắt AB và CD lần lượt tại K, H. Chứng minh tứ giác EKFH là hình bình hành.

Tìm tập hợp X sao cho \(\left\{ {a;\;b} \right\} \subset X \subset \left\{ {a;\;b;\;c;\;d} \right\}\).

a) Xác định các tập hợp X sao cho:\(\left\{ {a;\;b} \right\} \subset X \subset \left\{ {a;\;b;\;c;\;d;\;e} \right\}\).

b) Cho A = {1; 2}, B = {1; 2; 3; 4; 5}. Xác định các tập hợp X sao cho \(A \cup X = B\).

a) Tìm m để đường thẳng y = (m+2)x+m song song với đường thẳng y = 3x – 2.
b) Hãy vẽ đồ thị của hàm số \(y = - \frac{1}{4}{x^2}\).

Tìm m, n để đường thẳng y = mx + n song song với đường thẳng y = 3x + 2 và cắt trục hoành tại điểm có hoành độ là 2.

Kiểm tra rằng cặp số (x; y) = (2; −1) vừa là nghiệm của phương trình thứ nhất, vừa là nghiệm của phương trình thứ hai.

Cho phương tình 3x − 2y = 6. (1)

a) Viết công thức nghiệm tổng quát của phương trình (1);

b) Tìm nghiệm nguyên của phương trình (1).

1 tấn bằng bao nhiêu tạ? \[\frac{1}{5}\] tấn bằng bao nhiêu kg?

Cho tam giác ABC, trọng tâm G. Vẽ đường thẳng d đi qua G cắt các đoạn thẳng AB, AC. Goi A', B', C' thứ tự là hình chiếu của A, B, C trên d. Tìm liên hệ giữa các độ dài AA', BB', CC'.

Cho tam giác ABC, trọng tâm G.

a) Vẽ đường thẳng d qua G, cắt các đoạn thẳng AB, AC. Gọi A', B', C' là hình chiếu của A, B, C trên d. Tìm liên hệ giữa các độ dài AA', BB', CC'

b) Nếu đường thẳng d nằm ngoài tam giác ABC và G' là hình chiếu của G trên d thì các độ dài AA', BB', CC', GG' có liên hệ gì?

Một tổ công nhân có 8 người dự định làm xong 1 sân bóng chuyền trong 6 ngày nhưng sau đó người ta quyết định là xong sân bóng sớm hơn 2 ngày. Hỏi như vậy phải bổ sung thêm bao nhiêu công nhân?

Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB và SC. Tìm giao tuyến của (SMN) và (SBD).

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB, SC.
a) Tìm giao tuyến của hai mặt phẳng (ABN) và (SCD).
b) Chứng minh đường thẳng BN song song với mặt phẳng (SDM).
c) Xác định các điểm I, J lần lượt là giao điểm của đường thẳng AN và đường thẳng MN với mặt phẳng (SBD).
d) Tính tỉ số \(\frac{{IB}}{{IJ}}\).

Cho tam giác ABC có A(−5; 6), B(−4; −1), C(4; 3). Tìm tọa độ trung điểm I của AC. Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.

Cho tứ giác ABCD có \(\widehat B = \widehat D = 90^\circ \).

a) CMR: 4 điểm A, B, C, D cùng thuộc một đường tròn, tìm tâm đường tròn đó.

b) So sánh độ dài AC và BD. Tứ giác ABCD cần thêm điều kiện gì thì AC = BD

Tìm hiệu của số lớn nhất có ba chữ số và số bé nhất có ba chữ số khác nhau

Tìm hiệu của số lớn nhất có ba chữ số khác nhau và số bé nhất có ba chữ số khác nhau

Từ các chữ số 1, 2, 3, 4, 5 lập được bao nhiêu số tự nhiên gồm 3 chữ số phân biệt.

Từ các chữ số 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên gồm 2 chữ số khác nhau?

Cho hai biểu thức

\(A = \frac{{2\sqrt x - 1}}{{\sqrt x - 1}}\) và \(B = \frac{{\sqrt x }}{{\sqrt x - 1}} + \frac{3}{{\sqrt x + 1}} - \frac{{6\sqrt x - 4}}{{x - 1}}\), với x ≥ 0; x ≠ 1.

a) Tính A khi x = 25

b) Rút gọn biểu thức B

c) Đặt P = A.B. Tìm giá trị nguyên của x để P < 1

Cho \(A = \frac{{\sqrt x + 2}}{{\sqrt x }}\) và \(B = \frac{{\sqrt x }}{{\sqrt x - 2}}\)

Đặt P = A.B. Tìm các giá trị của x để \(\left| P \right| = P\)

Tính 155,7 : 45

Đặt tính rồi tính 155,9 : 45

Cho nửa đường tròn (O), đường kính AB; Ax là tiếp tuyến của nửa đường tròn. Trên nửa đường tròn lấy điểm D (D khác A,B). Tiếp tuyến tại D của (O) cắt Ax ở S.

a) Chứng minh SO//BD.

b) BD cắt AS ở C. Chứng minh SA=SC.

c) Kẻ DH vuông góc với AB; DH cắt BS tại E. Chứng minh E là trung điểm của DH.

Cho nửa đường tròn tâm O đường kính AB. Ax là tia tiếp tuyến của nửa đường tròn (Ax và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB), từ điểm C trên nửa đường tròn (C khác A, B) vẽ tiếp tuyến CM cắt Ax tại M, hạ CH vuông góc với AB, MB cắt (O) tại Q và cắt CH tại N.

a) Chứng minh MA² = MQ.MB
b) MO cắt AC tại I. Chứng minh tứ giác AIQM nội tiếp.
c) Chứng minh: IN ^CH.

Cho tam giác ABC cân ở A. Gọi I là giao điểm các đường phân giác.

a) Xác định vị trí tương đối của đường thẳng AC với đường tròn (O) ngoại tiếp ∆BIC

b) Gọi H là trung điểm của BC. Kẻ đường kính IK của đường tròn (O).

Chứng minh: \(\frac{{AI}}{{AK}} = \frac{{HI}}{{HK}}\).

Cho đường tròn (O; R) có đường kính AB. Vẽ các tiếp tuyến Ax, By của đường tròn (O), trên đường tròn (O) lấy một điểm E bất kì (E khác A, B). Tiếp tuyến tại E của đường tròn (O) cắt Ax, By lần lượt tại C, D.

a) CM: CD = AC + BD.

b) Vẽ EF vuông góc AB tại F, BE cắt AC tại K. CM: AF.BC = KE.EB.

c) EF cắt CB tại I. CM tam giác AFC đồng dạng với tam giác BFD, suy ra FE là tia phân giác của góc CFD.

d) EA cắt CF tại M. EB cắt DF tại N. CM: M, I, N thẳng hàng.

Cho đường tròn (O), đường kính AB, vẽ các tiếp tuyến Ax, By. Từ M trên đường tròn (M khác A,B) vẽ tiếp tuyến thứ ba nó cắt Ax ở C cắt By ở D. Gọi Nlà giao điểm của BC và AD.

a) CMR: \(\frac{{CN}}{{AC}} = \frac{{NB}}{{BD}}\).

b) CM: MN ^ AB.

c) CMR: \(\widehat {COD} = 90^\circ \).

Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB tới đường tròn (O) với A, B là các tiếp điểm.

a) Chứng minh bốn điểm A, B, M, O cùng thuộc một đường tròn.

b) Kẻ đường kính AC của đường tròn (O). Chứng minh OM // CB.

c) Vẽ BK vuông góc với AC tại K. Chứng minh: CK.OM = OB.CB.

d) Tiếp tuyến tại C của đường tròn (O) cắt AB tại D. Chứng minh OD ^CM.

Cho đường tròn tâm O và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB với đường tròn(A, B là các tiếp điểm). Đường thẳng d thay đổi đi qua M cắt đường tròn tại 2 điểm phân biệt C và D(C nằm giữa M và D)

a) Chứng minh tứ giác AMBO nội tiếp

b) Chứng minhMA²=MC.MD

c) Chứng minh đường tròn ngoại tiếp tam giác OCD luôn đi qua điểm cố định khác O

2(x − 1)=7+(−3)

Tìm x, biết:

a) \(\left| {x - 1,7} \right| = 2,3\).

b) \(\left| {x + \frac{3}{4}} \right| - \frac{1}{3} = 0\).

Trên đường tròn (O;R) vẽ dây cung BC cố định. Một điểm A di chuyển trên cung lớn BC. Hai đường cao AE và BF của tam giác ABC cắt nhau tại H.
a) Chứng minh tứ giác ABEF nội tiếp.
b) Chứng minh tam giác ABC đồng dạng tam giác EFC.
c) Đường thẳng AE cắt đường tròn (O) tại I. Chứng minh H và I đối xứng nhau qua BC.
d) Gọi K là hình chiếu của O trên BC. Chứng minh tỉ số \[\frac{{AH}}{{OK}}\]không đổi và H chạy trên một cung tròn cố định khi A chuyển động trên cung lớn BC.

Cho đường tròn tâm O và BC là dây cung không đi qua tâm. Trên tia đối của tia BC lấy điểm M sao cho M không trùng với B. Đường thẳng đi qua M cắt đường tròn (O) đã cho tại N và P (N nằm giữa M và P) sao cho O nằm trong PMC. Gọi A là điểm chính giữa của cung nhỏ NP. Các dây AB và AC lần lượt cắt NP tại D và E.

a) Chứng minh tứ giác BDEC nội tiếp.
b) Chứng minh MB.MC = MN.MP.

Giải hệ phương trình: \(\left\{ \begin{array}{l}6{x^2} - 3xy + x = 1 - y\\{x^2} + {y^2} = 1\end{array} \right.\)

Vẽ đồ thị hàm số\(y = - \frac{2}{3}x\)

a) Tìm trên đồ thị điểm A có tung độ bằng −2;

b) Tìm trên đồ thị điểm B có hoành độ bằng 4;

c) Tìm trên đồ thị điểm C có tung độ bằng 3 lần hoành độ;

d) Tìm trên đồ thị điểm D có tung độ và hoành độ đối nhau.

Cho đường thẳng (d): y = x − 2. Điểm A nằm trên (d) có hoành độ và tung độ đối nhau sẽ có tọa độ là (a; b).

Khi đó, a.b = …

Cho \[P = \frac{{\sqrt x }}{{\sqrt x + 2}}\]. Hãy so sánh P và \(\sqrt P \)

Cho \[P = \frac{{\sqrt x }}{{\sqrt x - 1}}\], với x > 1. Hãy so sánh P và \(\sqrt P \)

Tổng của hai số là 19,1. Nếu giảm số hạng thứ nhất đi 4 lần và giữ nguyên số hạng thứ hai thì được tổng mới là 7,4. Tìm hai số đó.

Có ba chiếc hộp A,B,C mỗi chiếc hộp chứa ba chiếc thẻ được đánh số 1,2, 3. Từ mỗi hộp rút ngẫu nhiên một chiếc thẻ. Gọi P là xác suất để tổng số ghi trên ba tấm thẻ là 6. Khi đó P bằng:

Chọn ngẫu nhiên ba số đôi một khác nhau từ tập hợp {1; 2; 3; ...; 100} gồm 100 số nguyên dương đầu tiên. Tính xác suất để 3 số được chọn là độ dài 3 cạnh của một tam giác.

Cho xÎ ℕ. Hãy chứng minh x² + 1 không chia hết cho 4.

Trong các mệnh đề sau, mệnh đề nào sai?

Cho tam giác ABC vuông tại A có đường cao AH.

Chứng minh rằng: \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\).

Cho 4 điểm O, A, B, C sao cho \(\overrightarrow {OA} + 2\overrightarrow {OB} - 3\overrightarrow {OC} = \overrightarrow 0 \).

Chứng minh: A, B, C thẳng hàng.

Một liên đội thiếu niên khi xếp hàng 2, hàng 3, hàng 4, hàng 5 đều thừa 1 người. Tính số đội viên của liên đội biết rằng số đội viên khoảng từ 100 đến 150?

Cho hàm số \(y = \frac{{2x - 1}}{{x - 1}}\;\left( C \right)\). Tìm m để (C) cắt d: y = x + m tại hai điểm phân biệt a,b sao cho tam giác OAB vuông tại A hoặc B.

Cho hàm số có đồ thị (C)\(y = \frac{{2x + 1}}{{x - 1}}\)và đường thẳng  d:y = x + m. Đường thẳng d cắt đồ thị (C) tại hai điểm A và B. Với C(−2; 5), giá trị của tham số m để tam giác ABC đều là bao nhiêu?

Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại C, AB = 2a, AC = a và SA vuông góc với mặt phẳng (ABC). Biết góc giữa hai mặt phẳng (SAB) và (SBC) bằng 60°. Tính thể tích của khối chóp S.ABC.

Cho hình chóp S.ABC có đường cao SA = 2a, tam giác ABC vuông ở C có AB = 2a, \(\widehat {CAB} = 30^\circ \). Gọi H là hình chiếu vuông của A trên SC. Tính theo a thể tích của khối chóp H.ABC. Tính cosin của góc giữa hai mặt phẳng (SAB), (SBC).

Phân tích đa thức thành nhân tử:

a) 7x²y − 14xy²+21x

b) 2x(x − y)+3y(y − x)

c) 6x(x − 3)+2x − 6

d) 4x(x − y)²+3x − 3y

Tính: (14xy² + 21x²y − 7x³) : 7x

Đọc tên góc, đỉnh, và các cạnh của góc trong các hình vẽ sau: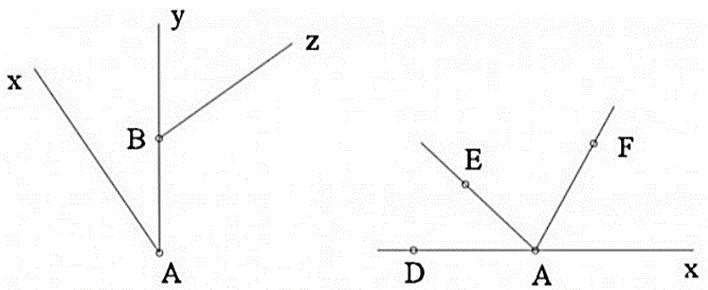

Đọc tên góc, đỉnh và các cạnh của góc trong Hình 85 và Hình 86.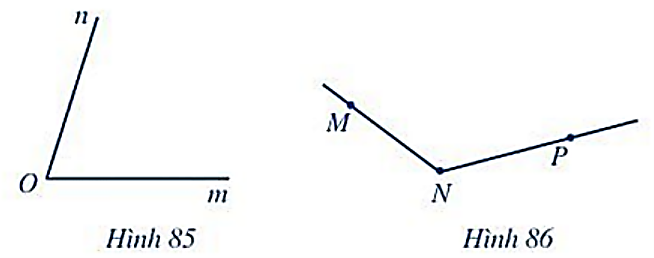

Phân tích thành nhân tử: x³ + y³ + z³ − 3xyz.

Cho hàm số y=(m − 1)x+3 có đồ thị là đường thẳng(d)
a) Vẽ đường thẳng(d) khi m=2
b) Tìm m để đường thẳng song song với đường thẳng y=2x+1
c) Tính khoảng cách là gốc tọa độ đến đường thẳng được vẽ ở ý(a)

Cho hàm số y=(m − 1)x−3 có đồ thị là (d) (m ≠ 1)
a) Vẽ đồ thị hàm số khi m = −2.
b) Tìm m để đồ thị hàm số cắt đường thẳng y = 2x + 5 tại điểm cỏ hoành độ bằng 4
c) Tìm m để đường thẳng (d) tạo với 2 trục tọa độ một tam giác có diện tích bằng 3

Số hạng nào chứa x với số mũ tự nhiên trong khai triển sau:

a) \({\left( {\sqrt[4]{x} + x} \right)^{10}}\)

b) \({\left( {x + \frac{1}{{\sqrt[3]{x}}}} \right)^{13}}\)

Giá trị nào của m để điểm I(−1;6) là điểm cực đại của đồ thị hàm số y = x³ − 3mx² − 9x + 1(Cm).

Biết M(1; −6) là điểm cực đại của đồ thị hàm số y=2x³+bx²+cx+1.Tìm tọa độ điểm cực tiểu của đồ thị hàm số đó.

Giải hệ phương trình:

\[\left\{ \begin{array}{l}x + y + xy = 11\\{x^2} + {y^2} + 3\left( {x + y} \right) = 28\end{array} \right.\]

Giải hệ phương trình:

\[\left\{ \begin{array}{l}xy + x + y = 11\\{x^2}y + x{y^2} = 30\end{array} \right.\]

Tìm 3 số hạng liên tiếp của một cấp số cộng, biết tổng của chúng là 27 và tổng các bình phương của chúng là 293.

Tìm cấp số cộng có 3 số hạng liên tiếp, biết tổng số của chúng là 15 và tổng bình phương các số hạng là 83.

Nêu tính chất đối xứng của hình vuông, hình chữ nhật, hình thoi, hình bình hành.

Hãy chỉ rõ tâm đối xứng của hình vuông, các trục đối xứng của hình vuông.