5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 17)

Cho biểu thức \(A = \frac{{\sqrt x - 1}}{{\sqrt x + 1}}\) và \(B = \frac{{\sqrt x + 6}}{{\sqrt x - 1}}\).

Đặt P = A.B. Tìm x hữu tỉ để P có giá trị nguyên nhỏ nhất.

Từ các chữ số 0; 1; 2; 3; 4; 5; 6; 8; 9, có thể lập được bao nhiêu số tự nhiên có 5 chữ số và lớn hơn 65000?

Xét tính bị chặn của dãy số (u_n) với \({u_n} = \frac{{2n + 1}}{{n + 1}}\).

Xét tính tăng hay giảm và bị chặn của dãy số: \({u_n} = \frac{{2n - 1}}{{n + 3}},\,n \in {\mathbb{N}^*}\).

Cho biểu thức \(A = \left( {\frac{{\sqrt x + 1}}{{\sqrt {xy} + 1}} + \frac{{\sqrt {xy} + \sqrt x }}{{1 - \sqrt {xy} }} + 1} \right):\left( {1 - \frac{{\sqrt {xy} + \sqrt x }}{{\sqrt {xy} - 1}} - \frac{{\sqrt x + 1}}{{\sqrt {xy} + 1}}} \right)\).

a) Rút gọn A.

b) Cho \(\frac{1}{{\sqrt x }} + \frac{1}{{\sqrt y }} = 6\). Tìm giá trị lớn nhất của A.

Cho hình bình hành ABCD, có AB = 2a, AD = a, \(\widehat {ABC} = 120^\circ \); quay hình bình hành xung quanh cạnh AD. Thể tích khối tròn xoay tạo thành là

Hình chóp S.ABCD có đáy là hình thoi, AB = 2a, \(\widehat {BAD} = 120^\circ \). Hình chiếu vuông góc của S lên (ABCD) là I, với I là giao điểm của hai đường chéo AC và BD, biết \(SI = \frac{a}{2}\). Tính thể tích khối chóp S. ABCD.

Cho tam giác ABC có 3 góc nhọn, AB < AC, đường cao AD, BE, CF cắt nhau tại H.

a) Chứng minh .

b) EF cắt CB tại M. Chứng minh MB.MC = ME.MF.

c) Biết S_ABC = 24, BD = 3 và CD = 5. Tính S_BHC.

Cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H.

a) Chứng minh và S_AEF = cos²A.S_ABC.

b) Gọi M là trung điểm của BC. Đường thẳng vuông góc với HM tại H cắt AB, AC lần lượt tại P và Q. Chứng minh PH = QH.

c) Chứng minh \(\cot A + \cot B + \cot C \ge \sqrt 3 \).

Chứng minh sin2a = 2sina.cosa.

Chứng minh hệ thức sau: \(\frac{{{{\left( {\sin a + \cos a} \right)}^2} - {{\left( {\sin a - \cos a} \right)}^2}}}{{\sin a.\cos a}} = 4\).

Một tổ chuyên môn tiếng Anh của trường đại học X gồm 7 thầy giáo và 5 cô giáo, trong đó thầy Xuân và cô Hạ là vợ chồng. Tổ chọn ngẫu nhiên 5 người để lập hội đồng chấm thi vấn đáp tiếng Anh B1 khung châu Âu. Xác suất sao cho hội đồng có 3 thầy, 2 cô và nhất thiết phải có thầy Xuân hoặc cô Hạ nhưng không có cả hai là

Một tổ chuyên môn gồm 7 thầy giáo và 5 cô giáo, trong đó thầy An và cô Bình là vợ chồng. Chọn ngẫu nhiên 5 người để lập hội đồng chấm thi vấn đáp. Có bao nhiêu cách lập sao cho hội đồng có 3 thầy, 2 cô và nhất thiết phải có thầy An hoặc cô Bình nhưng không có cả hai.

Cho A, B, C thẳng hàng và điểm M không thuộc đường thẳng đó. Gọi A’, B’, C’ lần lượt là điểm đối xứng của A, B, C qua M. Chứng minh A’, B’, C’ thẳng hàng.

Cho nửa đường tròn đường kính AB, C là một điểm thuộc nửa đường tròn, vẽ dây BD là phân giác của \[\widehat {ABC}\], BD cắt AC tại E, AD cắt BC tại G. H là điểm đối xứng với E qua D. Tứ giác AHGE là hình gì? Chứng minh AH là tiếp tuyến đường tròn.

Cho nửa đường tròn đường kính AB, C là một điểm thuộc nửa đường tròn. Vẽ dây BD là phân giác của \[\widehat {ABC}\], BD cắt AC tại E, AD cắt BC tại G. H là điểm đối xứng với E qua D. Chọn câu đúng:

Cho \(A = \frac{7}{{\sqrt x + 8}}\) và \(B = \frac{{\sqrt x + 8}}{{\sqrt x + 3}}\). Tìm x để P = A.B có giá trị là số nguyên.

Cho \(A = \frac{{{x^2} - 9}}{{3\left( {x + 5} \right)}}\) và \(B = \frac{3}{{x + 3}}\). Cho P = A.B. Tìm giá trị nguyên của x để P có giá trị nguyên.

Cho tam giác ABC có M là trung điểm của BC. Tính \(\overrightarrow {AB} \) theo \(\overrightarrow {AM} \) và \(\overrightarrow {BC} \).

Cho tứ diện ABCD. Trên cạnh AD, BC theo thứ tự lấy các điểm M, N sao cho \(\frac{{MA}}{{AD}} = \frac{{NC}}{{CB}} = \frac{1}{3}\). Gọi (P) là mặt phẳng chứa đường thẳng MN và song song với CD. Khi đó thiết diện của tứ diện ABCD cắt bởi mặt phẳng (P) là

Cho đoạn thẳng AB có trung điểm I. M là điểm tùy ý không nằm trên đường thẳng AB. Trên MI kéo dài, lấy một điểm N sao cho IN = MI.

a) Chứng minh \[\overrightarrow {BN} - \overrightarrow {BA} = \overrightarrow {MB} \].

b) Tìm các điểm D, C sao cho \(\overrightarrow {NA} + \overrightarrow {NI} = \overrightarrow {ND} ;\,\,\overrightarrow {NM} - \overrightarrow {BN} = \overrightarrow {NC} \).

Cô Hoàn mua 5 kg gạo tẻ và 5 kg gạo nếp. Giá 1 kg gạo tẻ là 9300 đồng, 1 kg gạo nếp là 11200 đồng. Hỏi cô Hoàn phải trả hết bao nhiêu tiền?

Với những giá trị nào của m thì đồ thị của các hàm số y = 12x + (5 – m) và y = 3x + (3 + m) cắt nhau tại một điểm trên trục tung?

Cho hàm số y = (m + 2)x + 2m² + 1. Tìm m để 2 đường thẳng (d): y = (m + 2)x + 2m² + 1 và (d’): y = 3x + 3 cắt nhau tại 1 điểm trên trục tung.

Một trang trại cần thuê xe vận chuyển 450 con lợn và 35 tấn cám. Nơi cho thuê xe chỉ có 12 xe lớn và 10 xe nhỏ. Một chiếc xe lớn có thể chở 50 con lợn và 5 tấn cám. Một chiếc xe nhỏ có thể chở 30 con lợn và 1 tấn cám. Tiền thuê một xe lớn là 4 triệu đồng, một xe nhỏ là 2 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí thuê xe là thấp nhất?

Rút gọn các phân thức sau:

a) \(\frac{{9 - 12x + 4{x^2}}}{{2x - 3}}\);

b) \(\frac{{{{\left( {2x + 3} \right)}^2} + 2\left( {4{x^2} - 9} \right) + {{\left( {2x - 3} \right)}^2}}}{{{{\left( {2x - 3} \right)}^2} - 2\left( {4{x^2} - 9} \right) + {{\left( {2x + 3} \right)}^2}}}\);

c) \(\frac{{{{\left( {2x + 3} \right)}^3} - {{\left( {2x - 3} \right)}^3}}}{{{{\left( {3x + 4} \right)}^2} + 3{x^2} - 24x - 7}}\);

d) \(\frac{{\left( {x + 1} \right)\left( {x + 2} \right)\left( {x + 3} \right)\left( {x + 4} \right) + 1}}{{{x^2} + 5x + 5}}\);

e) \(\frac{{{x^4} + 4}}{{x\left( {{x^2} + 2} \right) - 2{x^2} - {{\left( {x - 2} \right)}^2} - 1}}\).

Cho \(M = 2x - 3 - \sqrt {4{x^2} - 12x + 9} \).

a) Rút gọn M.

b) Tính M khi \(x = \frac{5}{2};\,x = \frac{{ - 1}}{5}\).

Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; –1) và B(3; 2). Tìm M thuộc trục tung sao cho MA² + MB² nhỏ nhất.

Từ một điểm A nằm bên ngoài đường tròn (O; R), vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Đường thẳng vuông góc với OB tại O cắt tia AC tại N. Đường thẳng vuông góc với OC tại O cắt AB tại M.

1) Xác định hình tính của tứ giác AMON.

2) Điểm A phải cách O một khoảng là bao nhiêu để MN là tiếp tuyến của (O)?

3) Tính diện tích tứ giác AMON.

Cho hình chóp S.ABCD, ABCD là hình bình hành, M là trung điểm của SA.

a) Xác định giao điểm của SB và (MCD).

b) Tìm thiết diện của hình chóp S.ABCD khi cắt bởi (MCD).

Tìm tất cả các giá trị thực của tham số m để phương trình x² – 5x + 7 + 2m = 0 có nghiệm thuộc đoạn [1; 5].

Tập xác định của hàm số \(y = \frac{{\cot x}}{{\sin x - 1}}\) là

Tìm tập xác định của hàm số:

a) y = cot(1 – x);

b) \(y = x + \frac{1}{{\left( {\sin x + 1} \right)\cot x}}\).

Tính A = sin²2° + sin²4° + sin²6° + … + sin²84° + sin²86° + sin²88°.

Tính giá trị biểu thức A = sin²1° + sin²2° + … + sin²88° + sin²89° + sin²90°.

Vẽ đồ thị hai hàm số trên cùng hệ trục tọa độ y = x² và y = 2x + 3.

a) Vẽ đồ thị hàm số y = –x² (P) và hàm số y = –2x – 3 (D) trên cùng hệ tọa độ.

b) Tìm tọa độ giao điểm của (P) và (D).

c) Gọi giao điểm (P) và (D) là A. Tính độ dài từ A đến B(5; –7).

Trong hình 97, biết diện tích miền gạch sọc là 86 cm². Tính diện tích hình tròn.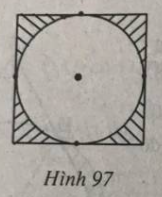

Chứng minh:

a) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C);

b) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).

Chứng minh:

a) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C);

b) (A \ B) \ C ⊂ A \ C.

Cho hình vuông ABCD cạnh a. Tính \(\left| {\overrightarrow {AD} + 3\overrightarrow {AB} } \right|\) theo a.

Tam giác ABC có AB = 3, AC = 6, \(\widehat {BAC} = 60^\circ \). Tính độ dài đường cao HA của tam giác.

Cho tam giác ABC có AB = 4, AC = 6, \(\widehat {BAC} = 60^\circ \). Tính (làm tròn kết quả đến hàng đơn vị):

a) Độ dài cạnh BC và độ lớn góc B;

b) Bán kính đường tròn ngoại tiếp R;

c) Diện tích của tam giác ABC;

d) Độ dài đường cao xuất phát từ A;

e) \(\overrightarrow {AB} .\overrightarrow {AC} ,\,\,\overrightarrow {AM} .\overrightarrow {AC} \), với M là trung điểm của BC.

Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của DA, BC. Tính góc giữa hai đường thẳng AB và CD biết AB = CD = 2a; \(MN = a\sqrt 3 \).

Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AD, BC.

a) Chứng minh \(\overrightarrow {MN} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {DC} } \right)\).

b) Xác định điểm O sao cho \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \vec 0\).

Tính \(\sqrt {6 - 2\sqrt 5 } \).

Chứng minh:

a) \(\overrightarrow {MN} + \overrightarrow {QE} + \overrightarrow {PQ} + \overrightarrow {NP} = \overrightarrow {ME} \);

b) \(\overrightarrow {AB} + \overrightarrow {MN} + \overrightarrow {BC} + \overrightarrow {CA} + \overrightarrow {PQ} + \overrightarrow {NM} = \overrightarrow {PQ} \);

c) \(\overrightarrow {FK} + \overrightarrow {MQ} - \overrightarrow {FP} - \overrightarrow {MP} + \overrightarrow {QK} = 2\overrightarrow {PK} \);

d) \(\overrightarrow {AD} + \overrightarrow {MP} + \overrightarrow {EK} - \overrightarrow {EP} - \overrightarrow {MD} = \overrightarrow {AK} \).

Cho bốn điểm M, N, P, Q. Chứng minh:

a) \(\overrightarrow {PQ} + \overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {MQ} \);

b) \(\overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {QP} + \overrightarrow {MQ} \);

c) \(\overrightarrow {MN} + \overrightarrow {PQ} = \overrightarrow {MQ} + \overrightarrow {PN} \).

Phân tích nhân tử x³ – y³.

Khai triển hằng đẳng thức: x³ + y³.

Cho tứ diện ABCD với \(AC = \frac{3}{2}AD,\,\,\widehat {CAB} = \widehat {DAB} = 60^\circ ,\,\,CD = AD\). Gọi φ là góc giữa hai đường thẳng AB và CD. Chọn khẳng định đúng về góc φ.

Cho hàm số bậc nhất y = (2m – 3)x + 5m – 1 (m là tham số, \[m \ne \frac{3}{2}\]).

a) Tìm m để hàm số nghịch biến trên ℝ.

b) Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ là –6.

c) Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ là –6.

Tìm tất cả các giá trị nguyên của tham số m ∈ [–3; 5] để hàm số y = (2m – 3)x + 5m – 1 nghịch biến trên ℝ.

Tìm tất cả các giá trị thực của tham số m để hàm số y = (m – 1)x⁴ – 2(m – 3)x² + 1 không có cực đại?

Tìm tất cả các giá trị thực của tham số m để hàm số \(y = \left( {m + 1} \right){x^4} - m{x^2} + \frac{3}{2}\) chỉ có cực tiểu mà không có cực đại.

Cho tam giác cân ABC có CA = CB và góc ABC nhọn. Các đường cao CD, BE, AF cắt nhau ở H.

a) Chứng minh 4 điểm C, F, H, E nằm trên đường tròn (O). Xác định tâm O của đường tròn.

b) Chứng minh (O) tiếp xúc với đường tròn ngoại tiếp tam giác ABC.

c) Chứng minh DF là tiếp tuyến của đường tròn (O).

d) Chứng minh FB là phân giác của góc DFE.

Cho hai hàm số y = –2x² (P) và y = 3x + m – 1 (d). Tìm m để (d) cắt (P) tại hai điểm nằm bên trái trục tung.

Tìm m để giao điểm của d: y = 12x + 5 – m; d’: y = 3x + m + 3 nằm bên trái trục tung.

Cho 4 điểm A, B, C, D bất kì. Gọi E, F lần lượt là trung điểm AB, CD, O là trung điểm EF. Chứng minh \(4\overrightarrow {AO} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \).

Cho 4 điểm A, B, C, D bất kì. Gọi E, F lần lượt là trung điểm AB, CD. O là trung điểm EF. Chứng minh rằng \(\overrightarrow {AD} + \overrightarrow {BC} = 2\overrightarrow {EF} \).

a) Tìm x, biết: x(x + 3) – x² + 9 = 0.

b) Thực hiện phép chia: A = 2x² + 3x – 2 cho B = 2x – 1.

Tìm x, biết: 2x(x – 3) + x² – 9 = 0.

Cho tam giác ABC vuông cân đỉnh A. Qua A kẻ đường thẳng d cắt BC. Vẽ BM, CN cùng vuông góc với d. Chứng minh ∆BAM = ∆ACN.

Cho tam giác ABC vuông tại A có AB = AC. Qua A vẽ đường thẳng d (B, C nằm cùng phía đối với d). Kẻ BM và CN vuông góc với d. Chứng minh rằng:

a) ∆BAM = ∆ACN;

b) MN = BM + CN.

Cho tam giác đều ABC cạnh a, điểm M là trung điểm BC. Dựng các vectơ sau và tính độ dài của chúng.

a) \(\frac{1}{2}\overrightarrow {CB} + \overrightarrow {MA} \);

b) \(\overrightarrow {BA} - \frac{1}{2}\overrightarrow {BC} \);

c) \(\frac{1}{2}\overrightarrow {AB} + 2\overrightarrow {AC} \);

d) \(\frac{3}{4}\overrightarrow {MA} - 2,5\overrightarrow {MB} \).

Cho tam giác đều ABC cạnh a, điểm M là trung điểm BC. Tính

a) \(\left| {\frac{1}{2}\overrightarrow {CB} + \overrightarrow {MA} } \right|\);

b) \(\left| {\overrightarrow {BA} + \frac{1}{2}\overrightarrow {BC} } \right|\);

c) \(\left| {\frac{3}{4}\overrightarrow {MA} - \frac{5}{2}\overrightarrow {MB} } \right|\);

d) \(\left| {\frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} } \right|\).

Khai triển \({\left( {\sqrt 5 - \sqrt[4]{7}} \right)^{124}}\). Có bao nhiêu số hạng hữu tỉ trong khai triển trên?

Cho đường tròn (O; R), đường kính MN. Qua M và N vẽ lần lượt hai tiếp tuyến (d) và (d’) với đường tròn (O). Một đường thẳng qua O cắt đường thẳng (d) ở A và cắt đường thẳng (d’) ở P. Từ O vẽ một tia vuông góc với AP và cắt đường thẳng (d’) ở B.

a) Chứng minh OA = OP.

b) Hạ OH vuông góc với AB. Chứng minh OH = R và AB là tiếp tuyến của đường tròn (O).

c) Chứng minh AM.BN = R².

d) Tìm vị trí của điểm A để diện tích tứ giác ABNM nhỏ nhất.

Cho đường tròn (O; R) và dây MN. Các tiếp tuyến của (O) tại M, N cắt nhau ở A. Qua M, kẻ đường thẳng song song với AN, cắt (O) tại điểm thứ hai là P. Q là giao điểm của AP và (O), K là giao điểm của MQ và AN. Chứng minh

a) AK² = KQ.KM.

b) K là trung điểm của AN.

Biểu thức \(\sqrt {\frac{1}{a}} \) có nghĩa khi nào?

Tam giác ABC có AB = AC, tia phân giác của \(\widehat A\) cắt BC tại D.

a) Chứng minh rằng AD vuông góc với BC.

b) Lấy điểm E thuộc cạnh AB, điểm F thuộc cạnh AC sao cho BE = CF. Chứng minh rằng DA là tia phân giác của \(\widehat {EDF}\).

Cho tam giác ABC có AB = AC. Tia phân giác \(\widehat A\) cắt BC tại D.

a) Chứng minh DB = DC.

b) Chứng minh AD vuông góc BC.

Cho tam giác ABC vuông tại A, kẻ đường cao AH. Từ H kẻ HD vuông AC, HE vuông AB. Gọi M, N lần lượt là trung điểm của các đoạn thẳng HB, HC. Chứng minh tứ giác DEMN là hình thang vuông.

Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HD vuông góc với AB và HE vuông góc với AC (D trên AB, E trên AC). Gọi O là giao điểm của AH và DE.

a) Chứng minh AH = DE.

b) Gọi P và Q lần lượt là trung điểm của BH và HC. Chứng minh tứ giác DEQP là hình thang vuông.

c) Chứng minh O là trực tâm của tam giác ABQ.

d) Chứng minh S_ABC = 2S_DEQP.

Giải phương trình \(x - 2\sqrt {x - 3} = 3\).