5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 16)
65 câu hỏi
Cho hàm số y = (2 – m)x + m + 1 (với m là tham số và m ≠ 2) có đồ thị là đường thẳng d.
a) Khi m = 0, hãy vẽ d trên trục tọa độ Oxy.
b) Tìm m để d cắt đường thẳng y = 2x – 5 tại điểm có hoành độ bằng 2.
c) Tìm m để d cùng với các trục tọa độ Ox, Oy tạo thành một tam giác có diện tích bẳng 2.
Cho hai đường thẳng (d1): y = 2x + 5 và (d2): y = (m + 1)x + m – 1
Tìm m để hai đường thẳng cắt nhau tại điểm của tung độ bằng 1.
Qua H(0; 4) vẽ đường thẳng song song với trục Ox cắt các đường thẳng y = –2x; y = x lần lượt tại Avà B. Tìm tọa độ A, B
Qua điểm K(0; 2) vẽ đường thẳng (d) song song với trục Ox. Đường thẳng (d) cắt các đường thẳng (1): y = – 2x và (2): y = 0,5x lần lượt tại A và B. Tìm tọa độ của các điểm A, B.
Tính tổng N=1+11+111+1111+....+11...1 (có n chữ số 1)
Tính tổng sau:
A = 1 + 11 + 111 + 1111 + ... + 11...1 (10 chữ số 1)
Cho tam giác ABC vuông tại A đường cao AH, I là trung điểm của AB. Lấy K đối xứng với B qua H. Qua A dựng đường thẳng song song với BC cắt HI tại D a) AKHD là hình gì? b) Chứng minh tứ giác AHBD là hình chữ nhật c) Tam giác ABC phải có thêm điều kiện gì để AHBD là hình vuông d) M là điểm đối xứng với A qua H. Chứng minhAK vuông góc với CM.
Cho tam giác ABC vuông tại A, đường cao AH. Gọi I là trung điểm của AH. Đường vuông góc với BC tại C cắt đường thẳng BI tại D. Chứng minh DA = DC
Lập bảng biến thiên và vẽ đồ thị hàm số y = – x2 – 4x + 1
Vẽ đồ thị các hàm số sau:
a) y = 2x2 + 4x – 1;
b) y = – x2 + 2x + 3;
c) y = – 3x2 + 6x;
d) y = 2x2 – 5.
Cho tam giác ABC. Gọi O là một điểm thuộc miền trong tam giác. Gọi M,N,P,Q lần lượt là trung điểm của OB, OC, AC, AB.
a) Chứng minh rằng MNPQ là hình bình hành.
b) Xác định vị trí O để MNPQ là hình chữ nhật.
Cho đường tròn (O; R) đường kính AB và tiếp tuyến Ax. Từ điểmC thuộc Ax kẻ tiếp tuyến thứ hai CD với đường tròn (O) (D là tiếp điểm).Gọi giao
điểm của CO và AD là I.
a) Chứng minh: CO ⊥ AD.
b) Gọi giao điểm của CB và đường tròn (O) là E (E ≠B). Chứng minh CE.CB =CI.CO.
c) Chứng minh: Trực tâm H của tam giác CAD di động trên đường cố định khi
điểm C di chuyển trên Ax.
Cho đường tròn (O; R), đường kính AB. Kẻ tiếp tuyến Ax với đường tròn tại A. Lấy điểm M thuộc tia Ax, kẻ tiếp tuyến MC với đường tròn (O) tại C (C khác A). Tiếp tuyến của đường tròn tại B cắt AC tại D và cắt MC tại F. Nối OM cắt AC tại E
a) Chứng minh tứ giác OBDE nội tiếp.
b) Chứng minh AC. AD = 4R2.
c) Chứng minh AB là tiếp tuyến của đường tròn ngoại tiếp ΔMOF.
Khoảng cách BC trong hình vẽ dưới đây bằng bao nhiêu mét, biết M và N lần lượt là trung điểm của AB và AC, MN = 5x – 18 (mét); BC = 4x + 1\(\frac{1}{2}\)98 (mét)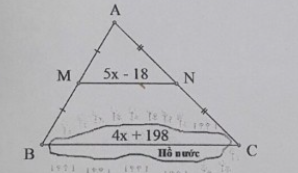
Chứng minh 1 . 2 + 2 . 5 + 3 . 8 + .... + n(3n – 1) = n2 (n+1) với mọi n thuộc N*.
Tính tổng :Sn = 1 . 2 + 2 . 5 + 3 . 8 + ....... + n(3n – 1).
Tìm số tự nhiên n sao cho: n2 + 3n + 6 chia hết n + 3
Tìm m để phương trình : x2 – 2mx + m – 1 = 0 có 2 nghiệm thỏa mãn x1 < 1 < x2.
Cho phương trình: (m + 1)x2 – 2(m – 1)x + m – 2 = 0. Xác định m để phương trình có nghiệm x1, x2 thỏa mãn \(\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} = \frac{7}{4}\).
Cho đường tròn (O; 2 cm) và điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA, MB kẻ từ M đến (O) vuông với nhau tại M.
a) Tứ giác MBOA là hình gì? Vì sao?
b) Gọi C là điểm bất kì trên cung nhỏ AB. Qua C kẻ tiếp tuyến với đường tròn cắt MA, MB theo thứ tự ở D và E. Tính chu vi tam giác MDE.
Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ hai tiếp tuyến MA, MB với (O) (A, B là các tiếp điểm). Qua M kẻ cát tuyến MCD với đường tròn (O) sao cho điểm C nằm giữa hai điểm M và D.
a) Chứng minh tứ giác MAOB nội tiếp.
b) Gọi H là giao điểm của MO và AB. Chứng minh MC . MD = MA2. Từ đó suy ra MC . MD = MH . MO.
c) Lấy K là trung điểm của CD. Gọi E là giao điểm của BA và OK. Chứng minh EC là tiếp tuyến của (O).
Giải các phương trình thuần nhất đối với sinx và cosx sau
a) sin2 x + sin 2x + 3cos2 x = 3
b) 3sin2 2x – 5sin 2x cos 2x – 8cos2 2x = 0
c) cos2 x – 3sin 2x cos 2x + 1 = 0
Cho tam giác ABC cân tại A, góc A bé hơn 90°. Kẻ AB vuông góc AC. Trên AB lấy E sao cho AE bằng AD. Chứng minh rằng:
a) DE song song BC.
b) CE vuông góc AB.
Cho tam giác ABC có \(\widehat A\)> 90°, kẻ AD vuông góc với AB, AD = AB (tia AD nằm giữa hai tia AB và AC), kẻ AE vuông góc với AC, AE = AC (tia AE nằm giữa hai tia AB, AC). Kẻ AH vuông góc với BC, AH kéo dài cắt DE tại M.
a) Chứng minh hai tam giác ABE; ADC bằng nhau và BE vuông góc với DC.
b) Từ D kẻ DP vuông góc với AM, từ E kẻ EQ vuông góc với AM. Chứng minh
DP = AH.
c) Chứng minh M là trung điểm của đoạn thẳng DE
d) Giả sử EQ = 3 cm; AQ = 4 cm. Từ Q hạ QI vuông góc với AE. Tính độ dài đoạn
thẳng AI; IE.
Cho tam giác ABC đều cạnh 2a. Khi đó độ dài vestơ \(\overrightarrow {AB} + \overrightarrow {AC} \) bằng
2a;
2a\(\sqrt 3 \);
4a;
a\(\sqrt 3 \).
Tính: 1 + 2 + 3 + ... + 99 + 100.
Giải phương trình : cos4 x + sin4 x = cos2x.
Chứng minh đẳng thức
a) cos4 x – sin4 x = cos2x.
b) cos4 x + sin4 x = \(\frac{3}{4} + \frac{1}{4}\)cos 4x.
c) \(\frac{{1 - c{\rm{os2x}}}}{{{\mathop{\rm s}\nolimits} {\rm{inx}}}}\)= tanx.
a) Hàm số \(y = \frac{{x + 1}}{{x - 2m + 1}}\) xác định trên [0; 1) khi m = ?
b) Hàm số \(y = \frac{{{x^2} - 3{\rm{x}}}}{{x - 2m - 1}}\) xác định trên [3; + ∞) khi m = ?
Tìm m để các phương trình sau có nghiệm duy nhất, vô nghiệm, vô số nghiệm
a) mx – 5 = 2x + m2 – 1
b) mx – 5 = 3x + m2 + 4
Cho biểu thức \({\rm{P = }}\frac{1}{{\sqrt x - 1}} - \frac{1}{{\sqrt x + 1}} - 1\) với x ≥ 0, x ≠ 1
a) Rút gọn P
b) Tìm tất cả các số nguyên x để P là một số nguyên.
Một chiếc cổng hình Parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ ở hai bên như hình vẽ. Biết chiều cao cổng Parabol là 4 m còn kích thước cửa ở giữa là 3m ×4m . Hãy tính khoảng cách giữa 2 điểm A và B.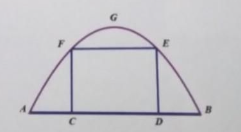
Một chiếc cổng hình Parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ ở hai bên như hình vẽ. Biết chiều cao cổng Parabol là 4 m còn kích thước cửa ở giữa là 3m ×6m . Hãy tính khoảng cách giữa 2 điểm A và B.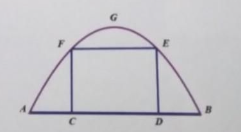
13 m
14 m
12 m
10 m.
Tính tổng: 2 + 4 + 6 + 8 + ... + 100
Biện luận m để (1 + m)x2 – 2mx + 2m = 0 có nghiệm.
Cho phương trình (1 + m)x2 – 2mx + 2m = 0. Tìm m để phương trình:
a) Có nghiệm;
b) Vô nghiệm;
c) Có 2 nghiệm;
d) Có 2 nghiệm phân biệt.
Cho hàm số: \(y = \frac{{mx}}{{\left( {2{m^2} + 1} \right){x^2} - 4mx + 2}}\).
Tìm mệnh đề đúng trong các mệnh đề sau:
Tồn tại giá trị của m để biểu thức không có nghĩa;
Hàm số luôn xác định với mọi m;
Số nguyên nhỏ nhất để hàm số xác định là m = 1;
Tất cả các mệnh đề trên đều sai.
Cho dãy số: 1, 2, 4, 7, 11, 16.... Số thứ 101 là số?
Cho dãy số: 1, 2, 4, 7, 11, 16. Hỏi số quy luật của dãy số trên?
Cho a, b, c > 0. Chứng minh rằng:
\(\frac{1}{{{a^2} + bc}} + \frac{1}{{{b^2} + ac}} + \frac{1}{{{c^2} + ab}} \le \frac{{a + b + c}}{{2{\rm{a}}bc}}\)
Cho tam giác ABC vuông tại A có AC = 6 cm , \(\widehat {ACB} = 30^\circ \) . Vẽ đường tròn (O) đường kính AC cắt BC tại D, dây DE vuông góc với AC tại H
a) Tính BC
b) Chứng minh tam giác CDE đều
c) Qua B vẽ đường thẳng tiếp xúc với (O) tại M. Chứng minh tam giác BDM đồng dạng với tam giác BMC
d) Gọi K là hình chiếu vuông góc của H trên EC và I là trung điểm của HK. Chứng minh DK vuông CI
Cho hình vuông ABCD cạnh a, tâm O. Khi đó \(\left| {\overrightarrow {{\rm{OA}}} - \overrightarrow {{\rm{BO}}} } \right|\) bằng :
a
\(\sqrt 2 \)a
\(\frac{a}{2}\)
2a.
Cho tam giác ABC cân ở A và H là trung điểm BC.Gọi I là hình chiếu vuông góc của H lên AC và O là trung điểm của HI. Chứng minh
a) \(\widehat {AHO} = \widehat {BCI}\)
b) AH . IC = HI . HC = HO . BC
c) Tam giác AHO đồng dạng tam giác BCI
d) AO vuông góc BI.
Cho tam giác ABC đều cạnh 2a, d là đường thẳng qua A và song song BC, khi M di động trên d thì giá trị nhỏ nhất của \(\left| {\overrightarrow {MA} + 2\overrightarrow {MB} - \overrightarrow {MC} } \right|\) là:
a\(\sqrt 3 \)
2a\(\sqrt 3 \)
\(\frac{{2{\rm{a}}\sqrt 3 }}{3}\)
\(\frac{{{\rm{a}}\sqrt 3 }}{3}\).
Cho hình bình hành ABCD. Gọi M và N lần lượt là trung điểm của AB và DC. AN và CM lần lượt cắt BD tại E và F. Chứng minh \(\overrightarrow {DE} = \overrightarrow {{\rm{EF}}} = \overrightarrow {FB} \)
Một hộp chứa 5 bi xanh, 7 bi đỏ và 8 bi vàng. Lấy ngẫu nhiên 8 viên bi từ hộp. Tính xác suất để 8 viên bi được lấy ra có đủ cả 3 màu.
\(\frac{{4539}}{{4975}}\)
\(\frac{{4529}}{{4845}}\)
\(\frac{{4539}}{{4845}}\)
\(\frac{{4539}}{{4945}}\)
Từ các chữ số 0; 1; 2; 3; 4; 5; 6 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số khác nhau và phải có mặt chữ số 5?
Từ các chữ số 1; 2; 3; 4; 5; 6; 7; 8; 9. Hỏi lập được bao nhiêu số tự nhiên có 6 chữ số sao cho số tạo thành nhất định phải có mặt chữ số 1, các chữ số khác chỉ xuất hiện nhiều nhất 1 lần và không có số nào có 2 chữ số 1 đứng cạnh nhau?
Cho a, b, c > 0 và a + b + c ≤\(\frac{3}{2}\).
Tìm giá trị nhỏ nhất của P = a + b + c + \(\frac{1}{a} + \frac{1}{b} + \frac{1}{c}\).
Cho a, b, c thỏa mãn a + b + c = \(\frac{3}{2}\).
Chứng minh rằng: a2 + b2 + c2 ≥ \(\frac{3}{4}\).
Cho tập hợp K = {5;6;7;8}. Viết các tập hợp con của K sao cho các phần tử của nó có ít nhất 1 số chẵn, 1 số lẻ.
Tính chiều cao của một cột tháp, biết rằng lúc mặt trời ở độ cao 50° (nghĩa là tia sáng của mặt trời tạo với phương nằm ngang của mặt đất một góc bằng 50°) thì bóng của nó trên mặt đất dài 96m.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy ABCD mặt bên (SCD) hợp với đáy góc 60 độ. Tính thể tích khối chóp S.ABCD.
Một đại lý có a sản phẩm. Nếu đại lý bán cho 83 cửa hàng thì mỗi cửa hàng có 1988 sản phẩm. Khi viết dấu phẩy ngay sau chữ số hàng nghìn của a thì đc số thập phân b. Số thập phân b có phần nguyên là ?
Cho hình bình hành ABCD (AB > AD). Qua A kẻ đường thẳng vuông góc với BD tại E, cắt CD tại I. Qua C kẻ đường thẳng vuông góc với AB tại F, cắt AB tại K.
a) Tứ giác AKCI là hình gì? Vì sao?
b) Chứng minh AF // CE
c) Chứng minh rằng ba đường thẳng AC, EF và KI đồng quy tại một điểm.
Một trường học có số học sinh xếp hàng 13, 17 lần lượt dư 4 em và 9 em, xếp hàng 5 thì vừa đủ. Tìm số học sinh của trường biết rằng số học sinh vào khoảng 2500 đến 3000 học sinh.
Chọn đáp án đúng:
Phân tích x3 – y3, ta được kết quả:
(x + y)(x – y)2
(x – y)(x2 + xy + y2)
(x + y)(x2 – xy + y2)
(x – y)(x2 + 2xy + y2)
Cho tam giác ABC. Hãy xác định các điểm I, J, K, L thỏa mãn các đẳng thức sau:
a) \(2\overrightarrow {IB} + 3\overrightarrow {IC} = \overrightarrow 0 \)
b) \(2\overrightarrow {J{\rm{A}}} + \overrightarrow {JC} - \overrightarrow {JB} = \overrightarrow {CA} \)
c) \(\overrightarrow {{\rm{KA}}} + \overrightarrow {KB} + \overrightarrow {KC} = 2\overrightarrow {BC} \)
d) \(3\overrightarrow {{\rm{LA}}} + 2\overrightarrow {LC} - \overrightarrow {LB} = \overrightarrow 0 \)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2sin x – 3cos x.
Tìm GTLN, GTNN của hàm số \(y = \frac{{2{\mathop{\rm s}\nolimits} {\rm{inx}} + 3}}{{{\rm{cosx }} - {\rm{ 4 }}}}\).
Cho đoạn thẳng AB có trung điểm I. M là điểm tùy ý không nằm trên đường thẳng AB. Trên MI kéo dài, lấy một điểm N sao cho IN = MI.
a) Chứng minh \(\overrightarrow {BN} - \overrightarrow {BA} = \overrightarrow {MB} \).
b) Tìm các điểm D, C sao cho\(\overrightarrow {NA} + \overrightarrow {NI} = \overrightarrow {N{\rm{D}}} ,\overrightarrow {NM} - \overrightarrow {BN} = \overrightarrow {NC} \).
Cho (O) đường kính AB, M ∈ (O). Tiếp tuyến tại M cắt tiếp tuyến tại A và B của (O) tại C và D và (I) đường kính CD. Chứng minh AB là tiếp tuyến của (I).
Cho đường tròn (O) có đường kính AB. Kẻ các tiếp tuyến với đường tròn tại A và B. Qua điểm M thuộc đường tròn (M khác A và B), kẻ tiếp tuyến với đường tròn, tiếp tuyến tại A và B lần lượt tại các điểm D và E, AE và BD cắt nhau tại H. Chứng minh rằng:
a) DE=AD+BE.
b) Tam giác DOE vuông tại O.
c) MH vuông góc với AB.
Một nhóm 4 đường thẳng song song cắt một nhóm 5 đường thẳng song song khác. Hỏi có bao nhiêu hình bình hành được tạo thành?
20
60
12
126.
Cho 5 đường thẳng song song với nhau và 4 đường thẳng khác song song, cắt 3 đường thẳng cho. Hỏi có bao nhiêu hình bình hành tạo nên bởi các giao điểm của các đường thẳng này.








