5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 13)

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(0; 1; 1) và B(1; 2; 3). Viết phương trình của mặt phẳng (P) đi qua A và vuông góc với đường thẳng AB.

Giải phương trình sau: 16,7.P_n = 2004.P_{n – 5}.

Điều kiện cần và đủ để điểm M(x; y) nằm trên đường thẳng d đi qua điểm M(x₀; y₀) và có vectơ pháp tuyến \(\vec n\left( {A,B} \right)\) là

Cho các số a, b, c khác nhau đôi một và thỏa mãn a² – 2b = b² – 2c = c² – 2a. Tính giá trị của biểu thức A = (a + b + 2)(b + c + 2)(c + a + 2).

Cho cấp số cộng (u_n) có số hạng tổng quát u_n = 3n – 1 (n ∈ ℕ*). Số hạng đầu u₁ và công sai d là

Cho hình vuông ABCD cạnh a, M bất kì. Chứng minh rằng các vectơ sau là vectơ không đổi. Tính độ dài của chúng:

a) \(2\overrightarrow {MA} - \overrightarrow {MB} - \overrightarrow {MC} \).

b) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} - 3\overrightarrow {MD} \).

c) \(4\overrightarrow {MA} - 3\overrightarrow {MB} + \overrightarrow {MC} - 2\overrightarrow {MD} \).

Cho tam giác nhọn ABC (AB < AC) nội tiếp trong đường tròn (O). Tiếp tuyến tại A của đường tròn (O) cắt đường thẳng BC tại M.

a) Chứng minh MA² = MB.MC.

b) Vẽ đường cao BD của tam giác ABC. Đường thẳng qua D và song song với MA cắt AB tại E. Chứng minh tứ giác BCDE nội tiếp và xác định tâm O’ của đường tròn ngoại tiếp.

c) Tia OO’ cắt đường tròn (O) tại N. Chứng minh AN là tia phân giác của góc BAC.

d) Gọi I, K lần lượt là giao điểm của AN với BD và CE. Tìm điều kiện của tam giác ABC để có \[\frac{{IB}}{{ID}}.\frac{{KC}}{{KE}} = \frac{{IB}}{{ID}} + \frac{{KC}}{{KE}}\].

Qua điểm M nằm ngoài (O), vẽ tiếp tuyến MA (A là tiếp điểm) và cát tuyến MBC (tia MO nằm giữa hai tia MA và MB).

a) Chứng minh MA² = MB.MC.

b) Kẻ AH vuông góc với OM tại H. Chứng minh MH.MO = MB.MC và tứ giác OHBC nội tiếp.

c) Tia BH cắt (O) tại điểm thứ hai là K. Chứng minh C đối xứng K qua đường thẳng OM.

Khảo sát sự biến thiên và vẽ đồ thị hàm số y = x² – 2x – 3.

Vẽ đồ thị hàm số f(x) = x² – 2x + 2.

Cho phương trình x² – mx + m – 3 = 0.

a) Chứng minh rằng phương trình đã cho luôn có 2 nghiệm phân biệt x₁, x₂.

b) Tìm hệ thức liên hệ giữa 2 nghiệm x₁, x₂ mà không phụ thuộc vào m.

Cho phương trình bậc hai ẩn x, tham số m: x² + mx + m + 3 = 0.

Tìm m để phương trình có 2 nghiệm trái dấu.

Tập hợp các số tự nhiên là gì?

Giải phương trình: \(\cos 2x - 3\cos x = 4{\cos ^2}\frac{x}{2}\).

Cho f(x) = ax² + bx + c. Tìm điều kiện của tham số m để f(x) < 0 với mọi x thuộc ℝ.

Phân tích đa thức thành nhân tử:

a) 3x² – 6xy + 3y² – 12;

b) 4x² – 4x + 1 – 9y²;

c) 9x² – 6x + 1 – 16y².

Phân tích đa thức sau thành nhân tử:

a) 3x² + 3y² – 6xy – 12;

b) x⁴ + x³ + 2x² + x + 1.

Cho hình vuông ABCD cạnh a. Tính \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\).

Cho hình vuông ABCD cạnh a. Tính \(\overrightarrow {AB} .\overrightarrow {AC} \).

Hình vẽ bên là một hình vuông ABCD có chu vi 48 dm. Tính diện tích phần tô đậm?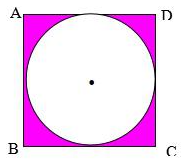

Tính bằng cách hợp lí: A = (–30) + (–29) + … + 48 + 49 + 50.

Cho tam giác ABC. Chứng minh rằng:

a) \(\cos \frac{A}{2} = \sqrt {\frac{{p\left( {p - a} \right)}}{{bc}}} \).

b) R ≥ 2r.

Tìm x, biết: (3x + 2)² – (1 – 2x)² = 0.

Giải các phương trình sau:

a) \(\frac{{x - 1}}{{59}} + \frac{{x - 2}}{{58}} + \frac{{x - 3}}{{57}} = \frac{{x - 4}}{{56}} + \frac{{x - 5}}{{55}} + \frac{{x - 6}}{{54}}\);

b) (3x – 2)² – (x + 3)² = 0;

c) x² – 9 = 2x + 6;

d) x³ + 9x² + 27x + 27 = 0.

Tìm x, y là số nguyên, biết:

a) x.y = 11;

b) (2x + 1)(3y – 2) = 12;

c) 1 + 2 + 3 + … + x = 55;

d) 6 ⋮(x – 1);

e) (2x + 1)³ = 27;

f) 2^x.16 = 128.

Giải phương trình: \(\sqrt[3]{{x - 2}} + \sqrt {x + 1} = 3\).

Một hộp chứa 6 viên bi đỏ và 4 viên bi xanh. Lấy lần lượt 2 viên bi từ hộp đó. Xác suất để viên bi được lấy lần thứ 2 là bi xanh bằng

Một hình chữ nhật có các kích thước 6 m và 2 m. Một hình tam giác có các cạnh bằng 5 m, 5 m, 6 m. Chứng minh rằng hai hình đó có chu vi bằng nhau và diện tích bằng nhau.

Viết phương trình của đường thẳng y = ax + b thỏa mãn một trong các điều kiện sau:

a) Có hệ số góc bằng –2 và đi qua điểm A(–1; 2).

b) Có tung độ gốc bằng 3 và đi qua một điểm trên trục hoành có hoành độ bằng –1.

c) Đi qua hai điểm B(1; 2) và C(3; 6).

Cho hình thoi ABCD có AB = BD. Gọi M, N lần lượt trên các cạnh AB, BC sao cho AM + NC = AD.

1) Chứng minh AM = BN.

2) Chứng minh ∆AMD = ∆BND.

3) Tính số đo các góc của ∆DMN.

Tìm nghiệm nguyên của phương trình x² + 5y² + 6z² + 2xy – 4xz = 10.

Cho đường tròn tâm O có bán kính OA = 8 cm, dây BC của đường tròn vuông góc với OA tại trung điểm I của OA. Tính BC.

Cho đường tròn tâm O, bán kính R = 8 cm và một điểm A có khoảng cách OA = 16 cm. Một đường kính BC quay xung quanh tâm O (đường thẳng BC không đi qua A). Đường tròn ngoại tiếp tam giác ABC cắt đường thẳng OA tại điểm thứ hai là D.

a) Chứng minh ∆OAB và ∆OCD đồng dạng.

b) Tính OD, suy ra D là điểm cố định khi đường kính BC quay xung quanh điểm O.

c) Giả sử AB cắt đường tròn (O) tại điểm thứ hai E và AC cắt đường tròn (O) tại điểm thứ hai F và gọi P là giao điểm của EF với OA. Chứng minh bốn điểm C, F, D, P cùng nằm trên một đường tròn. Có nhận xét gì về bốn điểm B, E, D, P?

Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Gọi O là giao điểm của MP, NQ. Gọi G là trọng tâm của tam giác BCD. Chứng minh A, O, G thẳng hàng.

Cho hàm số y = (2m – 1)x + 2 (1) có đồ thị là đường thẳng d_m.

a) Vẽ đồ thị hàm số m = 1.

b) Tìm m để hàm số (1) đồng biến trên ℝ.

c) Tìm m để d_m đồng quy với d₁: y = x + 4 và d₂: y = –2x + 7.

Cho hàm số bậc nhất: y = (2m + 1)x – 2 có đồ thị là đường thẳng (d).

a) Vẽ đồ thị hàm số với m = 1.

b) Tìm m để (d) song song với đồ thị hàm số: y = –4x + 1.

c) Tìm m để khoảng cách từ gốc tọa độ đến (d) bằng \(\sqrt 2 \).

Cho \[P = \frac{{2x + 2}}{{\sqrt x }} + \frac{{x\sqrt x - 1}}{{x - \sqrt x }} - \frac{{x\sqrt x + 1}}{{x + \sqrt x }}\,\,\,\left( {x > 0,\,x \ne 1} \right)\].

a) Rút gọn P.

b) So sánh P với 5.

c) Tìm x sao cho \(\frac{8}{P}\) nhận giá trị nguyên.

Cho biểu thức \(P = \frac{{2{x^2}}}{{{x^2} - 1}} + \frac{x}{{x + 1}} - \frac{x}{{x - 1}}\).

a) Tìm x để biểu thức P có nghĩa.

b) Rút gọn P.

c) Tính P tại x = –3.

d) Tìm giá trị nguyên của x để P có giá trị nguyên.

Tìm x ∈ ℤ, biết: 11 chia hết cho (2x + 1).

Tìm x ∈ ℕ để 11.2x chia hết cho 2x – 1.

Cho (O; R) và 3 dây AB, AC, AD; gọi M và N lần lượt là hình chiếu của B trên các đường thẳng AC, AD. Chứng minh MN ≤ 2R.

Giải phương trình:

a) \(\cos 2x + 2\cos x = 2{\sin ^2}\frac{x}{2}\).

b) 2cos²2x + 3sin²x = 2.

Cho hình thang cân ABCD (AB // CD) có đường chéo BD chia hình thang thành hai tam giác cân: tam giác ABD cân tại A và tam giác BCD cân tại D. Tính các góc của hình thang cân đó.

Công ty Bao bì Dược cần sản xuất 3 loại hộp giấy: đựng thuốc B₁, đựng cao Sao vàng, và đựng “Quy nhân sâm đại bổ hoàn”. Để sản xuất các loại hộp này, công ty dùng các tấm bìa có kích thước giống nhau. Mỗi tấm bìa có hai cách cắt khác nhau:

– Cách thứ nhất cắt được 3 hộp B₁, 1 hộp cao Sao vàng và 6 hộp Quy sâm.

– Cách thứ hai cắt được 2 hộp B₁, 3 hộp cao Sao vàng và 1 hộp Quy sâm.

Theo kế hoạch, số hộp Quy sâm phải có là 900 hộp, số hộp B₁ tối thiểu là 900 hộp, số hộp cao Sao vàng tối thiểu là 1000 hộp. Cần phương án sao cho tổng số bìa phải dùng là ít nhất?

Cho phương trình: \(1 + \tan x = 2\sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right)\). Tìm nghiệm x ∈ (0; 2π).

Cho đường tròn (O; R). Vẽ 2 dây AB và CD vuông góc với nhau. Chứng minh S_ACBD ≤ 2R².

Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau ở M. Biết AB = 14 cm; CD = 12 cm; MC = 2 cm. Bán kính R và khoảng cách từ tâm O đến dây CD lần lượt là

Cho phương trình x² – 2mx + 2(m – 2) = 0. Tìm m để phương trình có 2 nghiệm trái dấu sao cho nghiệm âm có giá trị tuyệt đối lớn hơn.

Cho phương trình (m – 4)x² – 2m(m – 2)x + m – 1 = 0. Định m để phương trình có hai nghiệm trái dấu và nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương.

Cho hình vuông ABCD có cạnh bằng a. Gọi E là trung điểm cạnh BC, F là trung điểm cạnh AE. Tìm độ dài đoạn thẳng DF.

Cho hình vuông ABCD có cạnh bằng a. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. M là giao điểm của CE và DF.

a) Chứng minh tứ giác EFGH là hình vuông.

b) Chứng minh DF ⊥ CE và ∆MAD cân.

c) Tính diện tích tam giác MDC theo a.

Tính bán kính đường tròn ngoại tiếp tam giác ABC, biết AB = 10 và \[\tan \left( {A + B} \right) = \frac{1}{3}\].

Cho nửa đường tròn (O) đường kính CD. Vẽ các tiếp tuyến Cx, Dy (Cx, Dy và nửa đường tròn (O) thuộc cùng một nửa mặt phẳng bờ CD). Lấy điểm M tùy ý trên nửa đường tròn trên. Tiếp tuyến tại M cắt Cx, Dy lần lượt tại A, B.

a) Chứng minh ∆OAB vuông tại O.

b) Chứng minh AB = AC + BD.

c) Chứng minh CD là tiếp tuyến của đường tròn đường kính AB.

Cho nửa đường tròn tâm O, đường kính CD. Từ C, D kẻ các tiếp tuyến Cx, Dy với nửa đường tròn tâm O. Trên nửa đường tròn lấy điểm E, điểm M bất kì nằm trên CD (M khác C, D, O). Qua E kẻ đường thẳng vuông góc với EM và cắt Cx, Dy tại A, B. Chứng minh \(\widehat {AMB} = 90^\circ \).

Trong các nhóm hình sau, nhóm nào có tâm đối xứng?

Nhóm hình nào đều có trục đối xứng?

Tìm ảnh của đường tròn (C): (x + 1)² + (y – 1)² = 4 qua:

a) Q_{(O; 90°)};

b) Q_{(O; 45°)}.

Tìm ảnh của (C): x² + y² + 2x – 84 = 0 qua Q_{(O; –45°)}.

Sơ đồ tư duy chương 4 hình học lớp 6.

Cách chuyển hỗn số thành số thập phân, ta làm như thế nào?