5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)

Cho a,b ≠ -2 thỏa mãn (2a + 1) (2b + 1) = 9

Tính giá trị biểu thức $M=\frac{1}{2+a}+\frac{1}{2+b}$.

Chứng minh các bất đẳng thức: $\frac{1}{a}+ \frac{1}{b}\ge \frac{4}{a+b}$ với a > 0, b > 0

Cho a lớn hơn 0 và b lớn hơn 0. Chứng minh rằng  _{$\left(\frac{1}{a}+\frac{1}{b}\right)\left(a+b\right)\ge 4$}

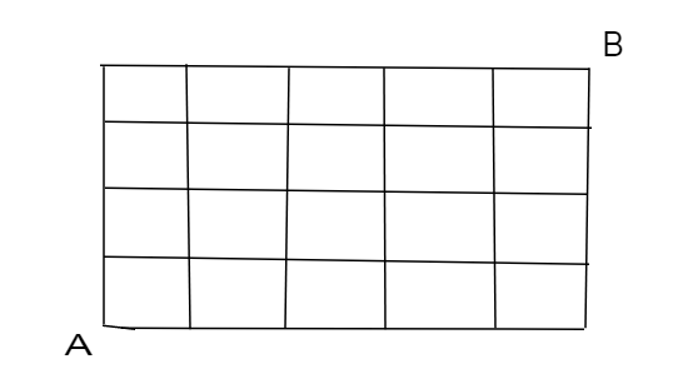
Trên bàn cờ 5 x 4 ô vuông như hình vẽ, người chơi chỉ được di chuyển quân theo các cạnh của hình vuông, mỗi bước đi được 1 cạnh. Có bao nhiêu cách di chuyển quân từ điểm A tới điểm B bằng 9 bước ?

Căn bậc hai của (a – b)² là:

Rút gọn

a) $\sqrt{{\left(\sqrt{2}-1\right)}^2}$;

b) $\sqrt{{\left(2-\sqrt{5}\right)}^2}$.

Tìm x

_{$3^{2x}-3^x=72$}

$2^x+2^x+1=72\left(x\in N\right)$ . Tìm x.

Cho $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0$. Tính giá trị biểu thức $P=\frac{ab}{c^2}+\frac{bc}{a^2}+\frac{ac}{b^2}$.

Cho a, b, c khác nhau đôi một và $\frac{\text{1}}{\text{a}}\text{+}\frac{\text{1}}{\text{b}}\text{+}\frac{\text{1}}{\text{c}}\text{=\hspace{0.17em}0}$. Rút gọn biểu thức:

a) $\text{M=}\frac{\text{1}}{{\text{a}}^{\text{2}}\text{+2bc}}\text{+}\frac{\text{1}}{{\text{b}}^{\text{2}}\text{+2ac}}\text{+}\frac{\text{1}}{{\text{c}}^{\text{2}}\text{+2ab}}\text{;}$

b) $\text{N=}\frac{\text{bc}}{{\text{a}}^{\text{2}}\text{+2bc}}\text{+}\frac{\text{ca}}{{\text{b}}^{\text{2}}\text{+2ac}}\text{+}\frac{\text{ab}}{{\text{c}}^{\text{2}}\text{+2ab}}\text{;}$

c) $\text{P=}\frac{{\text{a}}^{\text{2}}}{{\text{a}}^{\text{2}}\text{+2bc}}\text{+}\frac{{\text{b}}^{\text{2}}}{{\text{b}}^{\text{2}}\text{+2ac}}\text{+}\frac{{\text{c}}^{\text{2}}}{{\text{c}}^{\text{2}}\text{+2ab}}$.

Cho _{$\Delta ABC$} cân tại A, AM là đường cao. Gọi N là trung điểm của AC. D là điểm đối xứng của M qua N.

a) CMR : tứ giác ADCM là hình chữ nhật

b) CMR : tứ giác ABMD là hình bình hành và BD đi qua trung điểm O của AM

c) BD cắt AC tại I. CMR : $DI=\frac{2}{3}OB$

Hai số có hiệu là 95. Nếu xóa bỏ chữ số 5 ở tận cùng của số lớn thì ta được số bé. Tìm tổng hai số đó?

Lớp 10A có 45 học sinh trong đó có 25 em học giỏi môn Toán, 23 em học giỏi môn Lý, 20 em học giỏi môn Hóa, 11 em học giỏi cả môn Toán và môn Lý, 8 em học giỏi cả môn Lý và môn Hóa, 9 em học giỏi cả môn Toán và môn Hóa. Hỏi lớp 10A có bao nhiêu bạn học giỏi cả ba môn Toán, Lý, Hóa, biết rằng mỗi học sinh trong lớp học giỏi ít nhất một trong 3 môn Toán, Lý, Hóa?

Lớp 10A có 45 học sinh trong đó có 15 bạn được xếp lực học giỏi, 20 bạn được xếp hạnh kiểm tốt, có 10 bạn vừa được xếp lực học giỏi vừa được hạnh kiểm tốt. Số học sinh của lớp 10A được nhận khen thưởng nếu đạt được học lực giỏi hoặc hạnh kiểm tốt là:

A. 10.

B. 35.

C. 30.

D. 25.

Hình nón được tạo thành như thế nào? Nếu đặt mặt đáy của hình nón song song với mặt phẳng hính chiếu cạnh, thì hình chiếu đứng và hình chiếu cạnh có hình dạng gì?

Nếu đặt mặt đáy của hình nón song song với mặt phẳng chiếu cạnh thì hình chiếu đứng và hình chiếu cạnh có hình dạng:

A. Hình tròn, hình tam giác cân

B. Hình tam giác cân, hình tròn

C. Hình tròn, hình tam giác đều

D. Hình tam giác đều, hình tròn

Cho tam giác ABC đều. Gọi M, N lần lượt là các điểm trên cạnh AB, BC sao cho BM = BN. Gọi G là trọng tâm tam giác BMN và I là trung điểm của AN. Tính các góc của tam giác GIC.

Cho ΔABC, gọi I là giao điểm 3 đường phân giác trong. Qua I vẽ đường thẳng vuông góc AI cắt AB, AC tại M, N. Chứng minh rằng:

a) $\frac{BM}{CN}=\frac{B{I}^2}{C{I}^2}$

b) BM.AC + CN.AB + AI² = AB.AC

Cho hình vuông ABCD. O là giao điểm 2 đường chéo AC và BD. Gọi M, N lần lượt là trung điểm của OB, CD. Chứng minh góc AMN = 90°

Cho hình vuông ABCD. O là giao điểm 2 đường chéo AC và BD. Gọi M, N lần lượt là trung điểm của OB, CD.
a) Chứng minh góc AMN = 90°
b) A, M, N, D cùng thuộc 1 đường tròn
c) So sánh AN với MD

Tìm tất cả các giá trị của tham số m để khoảng cách từ điểm A (−1; 2) đến đường thẳng Δ: mx + y – m + 4 = 0 bằng $2\sqrt{5}$

Tìm tất cả các giá trị thực của tham số m để hàm số $y=x^3-3m{x}^2+3\left(m^2-1\right)x-m^3+m$ có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng $\sqrt{2}$ lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O

Có tam giác ABC vuông tại A đg cao AH, E, F lần lượt là hình chiếu của H lên AB, AC. CM: BE.AC + CF. AB = AH. BC

Cho tam giác ABC vuông tại A có AB = 3 cm; AC = 4 cm, đường cao AH. Gọi E, F lần lượt là hình chiếu của H lên AB, AC. Chứng minh rằng: AE. AB = AF. AC

Cho biết x và y là hai đại lượng tỉ lệ nghịch và khi x = 9 thì y = - 15

a) Tìm hệ số tỉ lệ nghịch của y đối với x

b) Hãy biểu diễn y theo x

c) Tính giá trị của y khi x = - 5, x = 18

Cho biết x và y là hai đại lượng tỉ lệ thuận, khi x = 10 thì y = 5 vậy khi x = - 5 thì giá trị của y bằng bao nhiêu?

Giải các phương trình sau

a) $x^2-6x+\sqrt{x^2-6x+7}=5$

b) $\sqrt{x+1}+\sqrt{x+6}=5$

c) _{$\sqrt{x+3-4\sqrt{x-1}}+\sqrt{x+8-6\sqrt{x-1}}=4$}

Tìm các cặp số nguyên x,y thỏa mãn x³ – 6x² + 12x = y³ + 27

Từ các chữ số: 1, 2, 3, 4, 5, 6, 7. Hỏi có thể lập được bao nhiêu số có 6 chữ số khác nhau mà chữ số 1 không đứng cạnh chữ số 6

Từ các số của tập A = {1; 2; 3; 4; 5; 6; 7} lập được bao nhiêu số tự nhiên gồm năm chữ số đôi một khác nhau, đồng thời hai chữ số 2 và 3 luôn đứng cạnh nhau

Cho tam giác ABC vuông tại A, có AB < AC, trên cạnh BC lấy điểm D sao cho BD = BA. Kẻ AH vuông góc BC, DK vuông góc AC. 
a) C/m góc BAD = góc BDA
b) C/m AD là phân giác của góc HAC
c) C/m AK = AH
d) C/m AB + AC < BC + AH

Cho tam giác ABC vuông góc tại A,có AB = AC.Gọi K là trung điểm của cạnh BC

a) Chứng minh tam giác AKB = tam giác AKC và AK vuông góc với BC.

b) Từ C kẻ đường thẳng vuông góc với BC, cắt AB tại E. Chứng minh EC song song với AK.

c) Chứng minh CE = CB.

Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hóa, 6 học sinh giỏi cả Toán và Lý, 5 học sinh giỏi cả Hóa và Lý, 4 học sinh giỏi cả Toán và Hóa, 3 học sinh giỏi cả ba môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A là:

Lớp 10A có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hoá, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hoá, 2 học sinh giỏi cả Lý và Hoá, 1 học sinh giỏi cả ba môn Toán, Lý, Hoá. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hoá ) của lớp 10A là:

Cho tam giác ABC. Có AB nhỏ hơn AC trên cạnh AB lấy điểm E sao cho BE =AC. Gọi I , D,F lần lượt là trung điểm của CE, AE , BC chứng minh 

a) tam giác IDF cân

b) góc BAC= 2IDF

Cho tam giác ABC . Trên các cạnh AB và AC lần lượt lấy hai điểm D và E sao cho BD = CE . Gọi M, N, P, Q thứ tự là trung điểm của BE, CD, DE và BC . Chọn câu đúng nhất.

Nêu khái niệm hình chiếu? Cho ví dụ và phân tích?

Cho tam giác ABC cố định (AB < AC). Hai điểm D, E theo thứ tự chuyển động trên các cạnh BA, CA sao cho BD + CE = a < AB.. Các trung điểm M của DE nằm trên đường nào?

Cho 4 điểm phân biệt A, B, C, D. Có bao nhiêu vectơ khác vectơ – không được lập ra từ 4 điểm đã cho?

Trong không gian cho 4 điểm A,B,C,D. Từ các điểm trên ta có thể lập được bao nhiêu vectơ khác vectơ không?

$\sqrt{3-\sqrt{5}}-\sqrt{3+\sqrt{5}}$. Tính và rút gọn

Cho tam giác ABC vuông tại A gọi M là trung điểm BC biết BC =13 tính AM

Cho tam giác ABC vuông tại A có M là trung điểm của BC

a) cho BC = 10cm tính AM

b) gọi N là trung điểm của AB cho MN // AC

c) kẻ MD // AD chứng minh tứ giác ANMD là hình chữ nhật

Cho tập hợp A = {0; 1; 2; 3; 4; 5}. Có thể lập bao nhiêu số tự nhiên chẵn có 4 chữ số khác nhau?

Với các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên chẵn gồm 5 chữ số khác nhau

Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm AB, BC, CD, DA. Khẳng định nào sau đây đúng.

Cho tứ giác ABCD có M , N , P , Q lần lượt là trung điểm của AB , BC , CD , DA . Chứng minh tứ giác MNPQ là hình bình hành , IMPN là hình bình hành

Cho các số 0;1;2;3;4;5;6;7. Từ các chữ số trên lập được bao nhiêu số có 4 chữ số đôi một khác nhau và chia hết cho 10

Số các số có 4 chữ số đôi một khác nhau được tạo thành từ các chữ số 2, 4, 6, 7, 8, 9 là:

Một trang trại cân thuê xe vận chuyển 450 con lợn và 35 tấn cám. Nơi cho thuê xe chỉ có 12 xe lớn và10 xe nhỏ. Một chiếc xe lớn có thể chở 50 con lợn và 5 tấn cám. Một chiếc xe nhỏ có thể chở 30 con lợn và 1 tấn cám. Tiền thuê một xe lớn là 4 triệu đồng, một xe nhỏ là 2 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí thuê xe là thấp nhất?

Chứng minh rằng: D = 1 + 4 + 4² + 4² + ... + 4⁵⁸ + 4⁵⁹ chia hết cho 21.

Cho A = 1 + 4 + 42 + 43 +...+ 411. Chứng tỏ rằng:a) A chia hết cho 21;b) A chia hết cho 105;c) A chia hết cho 4097.

Người ta dùng mấy hình chiếu để biểu diễn khối tròn xoay?  

x² – 16 + 4y² + 4xy. Phân tích đa thức thành nhân tử

Phân tích đa thức thành nhân tử 16 - x² - 4xy - 4y²

Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là chân đường vuông góc hạ từ H xuống AB và AC
a. CMR: ER = AH
b.Kẻ trung tuyến Am của tam giác ABC. C/m: AM⊥ EF

Một gương phẳng hình tròn đường kính 10 cm đặt trên bàn cách trần nhà 2m mặt phản xạ hướng lên . Ánh sáng từ bóng đèn bin (nguồn sáng điểm) cách trần nhà 1m

a, Hãy tính đường kính vệt sáng trên trần nhà

b. Cần phả dịch bóng đèn về phía nào vuông góc với gương một đoạn bao nhiêu để đường kính vệt sáng tăng gấp đôi

Cho tam giác ABC. Tìm tập hợp các điểm M sao cho: $\left|2\left(MA+MB+MC\right)\right|=\left|3\left(MB+MC\right)\right|$

Cho DABC. Tìm tập hợp điểm M trong các trường hợp sau:

$\left|2\overrightarrow{MA}+3\overrightarrow{MB}\right|=\left|3\overrightarrow{MB}-2\overrightarrow{MC}\right|$

Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành 2 đoạn: BH = 4cm và HC = 6cm.
a) Tính độ dài các đoạn AH, AB, AC
b) Gọi M là trung điểm của AC. Tính số đó góc AMB (làm tròn đến độ)
c) Kẻ AK vuông góc BM (K thuộc BM). Chứng minh: $\frac{BK}{BH}=\frac{BC}{BM}$

Cho điểm M có hoành độ là -2 và điểm M thuộc đồ thị hàm số y = −2x² . Xác định tọa độ điểm M

Cho hàm số y = x - 2 có đồ thị là d.Tìm điểm trên d có hoành độ và tung độ đối nhau

Cho tam giác ABC vuông tại A. Trên cạnh AC lấy M: 2MC < AC và M không trùng với C, vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng:

a) Tứ giác ABCD nội tiếp.

b) CA là phân giác góc SCB.

Cho đường tròn tâm O bán kỉnh và hai dây AB, CD bất kì. Gọi M là điểm chính giữa của cung nhỏ AB. Gọi E và F tương ứng là giao điểm của MC, MD với dây AB. Gọi I và J tương ứng là giao điểm của DE, CF với đường tròn (O). Chứng minh IJ song song với AB ?

Tìm chữ số tận cùng của các số: 
a) 7⁹⁹                   

b) 14¹⁴¹⁴                   

c) 4⁵⁶⁷

Cho hàm số y = 3x⁴ + 2(m − 2018)x² + 2017 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có ba điểm cực trị tạo thành tam giác có một góc bằng 120°

Cho hs: y = x⁴ + 2mx² + m² + m,    (1). ( m là tham số)
Xác định m để hs (1) có 3 cực trị, đồng thời các điểm cực trị của đồ thị tạo thành 1 tam giác có góc bằng 120 độ.

Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.

a) Tính độ dài các đoạn thẳng AB, AC, AH.

b) Trên cạnh AC lấy điểm K (K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK = BH.BC.

c) Chứng minh rằng: $S_{BHD}=\frac{1}{4}{S}_{BKC}.{\cos }^2\widehat{ABD}$.

Hai số có hiệu là 95. Nếu xóa bỏ chữ số 5 ở tận cùng của số lớn thì ta được số bé. Tìm tổng hai số đó?

Lớp 10A có 45 học sinh trong đó có 25 em học giỏi môn Toán, 23 em học giỏi môn Lý, 20 em học giỏi môn Hóa, 11 em học giỏi cả môn Toán và môn Lý, 8 em học giỏi cả môn Lý và môn Hóa, 9 em học giỏi cả môn Toán và môn Hóa. Hỏi lớp 10A có bao nhiêu bạn học giỏi cả ba môn Toán, Lý, Hóa, biết rằng mỗi học sinh trong lớp học giỏi ít nhất một trong 3 môn Toán, Lý, Hóa?

Lớp 10A có 45 học sinh trong đó có 15 bạn được xếp lực học giỏi, 20 bạn được xếp hạnh kiểm tốt, có 10 bạn vừa được xếp lực học giỏi vừa được hạnh kiểm tốt. Số học sinh của lớp 10A được nhận khen thưởng nếu đạt được học lực giỏi hoặc hạnh kiểm tốt là:

Hình nón được tạo thành như thế nào? Nếu đặt mặt đáy của hình nón song song với mặt phẳng hính chiếu cạnh, thì hình chiếu đứng và hình chiếu cạnh có hình dạng gì?

Nếu đặt mặt đáy của hình nón song song với mặt phẳng chiếu cạnh thì hình chiếu đứng và hình chiếu cạnh có hình dạng:

Cho tam giác ABC đều. Gọi M, N lần lượt là các điểm trên cạnh AB, BC sao cho BM = BN. Gọi G là trọng tâm tam giác BMN và I là trung điểm của AN. Tính các góc của tam giác GIC.

Cho ΔABC, gọi I là giao điểm 3 đường phân giác trong. Qua I vẽ đường thẳng vuông góc AI cắt AB, AC tại M, N. Chứng minh rằng:

a) $\frac{BM}{CN}=\frac{B{I}^2}{C{I}^2}$

b) BM.AC + CN.AB + AI² = AB.AC

Cho hình vuông ABCD. O là giao điểm 2 đường chéo AC và BD. Gọi M, N lần lượt là trung điểm của OB, CD. Chứng minh góc AMN = 90°Cho hình vuông ABCD. O là giao điểm 2 đường chéo AC và BD. Gọi M, N lần lượt là trung điểm của OB, CD.
a) Chứng minh góc AMN = 90°
b) A, M, N, D cùng thuộc 1 đường tròn
c) So sánh AN với MD

Tìm tất cả các giá trị của tham số m để khoảng cách từ điểm A (−1; 2) đến đường thẳng Δ: mx + y – m + 4 = 0 bằng $2\sqrt{5}$

Cho tam giác ABC vuông tại A có AB = 3 cm; AC = 4 cm, đường cao AH. Gọi E, F lần lượt là hình chiếu của H lên AB, AC. Chứng minh rằng: AE. AB = AF. AC

Cho biết x và y là hai đại lượng tỉ lệ nghịch và khi x = 9 thì y = - 15

a) Tìm hệ số tỉ lệ nghịch của y đối với x

b) Hãy biểu diễn y theo x

c) Tính giá trị của y khi x = - 5, x = 18

Cho biết x và y là hai đại lượng tỉ lệ thuận, khi x = 10 thì y = 5 vậy khi x = - 5 thì giá trị của y bằng bao nhiêu?

Tìm các cặp số nguyên x,y thỏa mãn x³ – 6x² + 12x = y³ + 27

Tính $\frac{x^2-6x+9}{x^2-3x+9}.\frac{x^3+27}{3x-9}$.

Từ các chữ số: 1, 2, 3, 4, 5, 6, 7. Hỏi có thể lập được bao nhiêu số có 6 chữ số khác nhau mà chữ số 1 không đứng cạnh chữ số 6

Từ các số của tập A = {1; 2; 3; 4; 5; 6; 7} lập được bao nhiêu số tự nhiên gồm năm chữ số đôi một khác nhau, đồng thời hai chữ số 2 và 3 luôn đứng cạnh nhau

Cho tam giác ABC vuông tại A, có AB < AC, trên cạnh BC lấy điểm D sao cho BD = BA. Kẻ AH vuông góc BC, DK vuông góc AC. 
a) C/m góc BAD = góc BDA
b) C/m AD là phân giác của góc HAC
c) C/m AK = AH
d) C/m AB + AC < BC + AH

Cho tam giác ABC vuông góc tại A,có AB = AC.Gọi K là trung điểm của cạnh BC

a) Chứng minh tam giác AKB = tam giác AKC và AK vuông góc với BC.

b) Từ C kẻ đường thẳng vuông góc với BC, cắt AB tại E. Chứng minh EC song song với AK.

c) Chứng minh CE = CB.

Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hóa, 6 học sinh giỏi cả Toán và Lý, 5 học sinh giỏi cả Hóa và Lý, 4 học sinh giỏi cả Toán và Hóa, 3 học sinh giỏi cả ba môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A là:

Lớp 10A có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hoá, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hoá, 2 học sinh giỏi cả Lý và Hoá, 1 học sinh giỏi cả ba môn Toán, Lý, Hoá. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hoá ) của lớp 10A là:

Cho tam giác ABC. Có AB nhỏ hơn AC trên cạnh AB lấy điểm E sao cho BE =AC. Gọi I , D,F lần lượt là trung điểm của CE, AE , BC chứng minh 

a) tam giác IDF cân

b) góc BAC= 2IDF

Cho tam giác ABC . Trên các cạnh AB và AC lần lượt lấy hai điểm D và E sao cho BD = CE . Gọi M, N, P, Q thứ tự là trung điểm của BE, CD, DE và BC . Chọn câu đúng nhất.

Nêu khái niệm hình chiếu? Cho ví dụ và phân tích?

Cho tam giác ABC cố định (AB < AC). Hai điểm D, E theo thứ tự chuyển động trên các cạnh BA, CA sao cho BD + CE = a < AB.. Các trung điểm M của DE nằm trên đường nào?

Cho 4 điểm phân biệt A, B, C, D. Có bao nhiêu vectơ khác vectơ – không được lập ra từ 4 điểm đã cho?

Trong không gian cho 4 điểm A,B,C,D. Từ các điểm trên ta có thể lập được bao nhiêu vectơ khác vectơ không?

$\sqrt{3-\sqrt{5}}-\sqrt{3+\sqrt{5}}$. Tính và rút gọn

Cho tam giác ABC vuông tại A gọi M là trung điểm BC biết BC =13 tính AM

Cho tam giác ABC vuông tại A có M là trung điểm của BC

a) cho BC = 10cm tính AM

b) gọi N là trung điểm của AB cho MN // AC

c) kẻ MD // AD chứng minh tứ giác ANMD là hình chữ nhật

Cho tập hợp A = {0; 1; 2; 3; 4; 5}. Có thể lập bao nhiêu số tự nhiên chẵn có 4 chữ số khác nhau?

Với các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên chẵn gồm 5 chữ số khác nhau

Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm AB, BC, CD, DA. Khẳng định nào sau đây đúng.

Cho tứ giác ABCD có M , N , P , Q lần lượt là trung điểm của AB , BC , CD , DA . Chứng minh tứ giác MNPQ là hình bình hành , IMPN là hình bình hành

Cho các số 0;1;2;3;4;5;6;7. Từ các chữ số trên lập được bao nhiêu số có 4 chữ số đôi một khác nhau và chia hết cho 10

Số các số có 4 chữ số đôi một khác nhau được tạo thành từ các chữ số 2, 4, 6, 7, 8, 9 là:

Một trang trại cân thuê xe vận chuyển 450 con lợn và 35 tấn cám. Nơi cho thuê xe chỉ có 12 xe lớn và10 xe nhỏ. Một chiếc xe lớn có thể chở 50 con lợn và 5 tấn cám. Một chiếc xe nhỏ có thể chở 30 con lợn và 1 tấn cám. Tiền thuê một xe lớn là 4 triệu đồng, một xe nhỏ là 2 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí thuê xe là thấp nhất?

Chứng minh rằng: D = 1 + 4 + 4² + 4² + ... + 4⁵⁸ + 4⁵⁹ chia hết cho 21.

Cho A = 1 + 4 + 4² + 4³ +...+ 4¹¹

a. Chứng tỏ rằng A chia hết cho 21

b. A chia hết cho 105

c. A chia hết cho 4097

Người ta dùng mấy hình chiếu để biểu diễn khối tròn xoay?  

 x² – 16 + 4y² + 4xy. Phân tích đa thức thành nhân tử

Phân tích đa thức thành nhân tử 16 - x² - 4xy - 4y²

Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là chân đường vuông góc hạ từ H xuống AB và AC
a. CMR: ER = AH
b.Kẻ trung tuyến Am của tam giác ABC. C/m: AM⊥ EF

Một gương phẳng hình tròn đường kính 10 cm đặt trên bàn cách trần nhà 2m mặt phản xạ hướng lên . Ánh sáng từ bóng đèn bin (nguồn sáng điểm) cách trần nhà 1m

a, Hãy tính đường kính vệt sáng trên trần nhà

b. Cần phả dịch bóng đèn về phía nào vuông góc với gương một đoạn bao nhiêu để đường kính vệt sáng tăng gấp đôi

Cho hình bình hành ABCD có diện tích là S. Gọi M là trung điểm của BC. Gọi N là giao điểm của AM và BD. Tính diện tích tứ giác MNDC theo S.

Có bao nhiêu số nguyên âm m để hàm số $\text{y = }\frac{\text{1}}{\text{3}}{\text{cos}}^{\text{3}}\text{x - 4cotx - }\left(\text{m + 1}\right)\text{ cosx}$ đồng biến trên khoảng $\left(0;\pi \right)$?

Tìm x ∈ BC(16; 21; 25) và x ≤ 400

Tìm các số tự nhiên x, biết:

a) x$\in$BC(30, 45), x < 500;

b) x $\in$BC(34, 85), 500 < x < 1000;

c) x $\in$BC(12, 21, 28), 150 < x < 300;

d)  x $\in$BC(65, 45, 105) và x là số có bốn chữ số;

e) x39; x 65, x 91 và 400 < x < 2600.

Cho đường tròn tâm O, đường kính AB và một điểm C di động trên đoạn AB. Vẽ các đường tròn tâm I đường kính AC và đường tròn tâm K đường kính BC. Tia Cx vuông góc với AB tại C, cắt (O) tại M. Đoạn thẳng MA cắt đường tròn (I) tại E và đoạn thẳng MB cắt đường tròn (K) tại F

a. Chứng minh tứ giác MECF là hình chữ nhật và EF là tiếp tuyến chung của (I) và (K)

b. Cho AB = 4cm, xác định vị trí điểm C trên AB để diện tích tứ giác IFEK là lớn nhất.

c. Khi C khác O, đường tròn ngoại tiếp hình chữ nhật MECF cắt đường trong (O) tại P (khác M), đường thẳng PM cắt đường thẳng AB tại N. Chứng minh tam giác MPF đồng dạng với tam giác MBN.

d. Chứng minh 3 điểm: N, E, F thẳng hàng

Cho đường tròn (O) đường kính AB, vẽ góc ở tâm $\widehat{AOC}={55}^0$. Vẽ dây CD vuông góc với AB và dây DE song song với AB. Tính số đo cung nhỏ BE.

Cho tam giác ABC lấy M bất kì trên cạnh BC. Từ M kẻ đường song song với AB cắt AC tại D. Từ M kẻ đường thẳng song song với AC cắt AB tại E.

Chứng minh: ME = AD và MD = AE.

Cho tam giác ABC vuông tại A. Từ điểm M bất kì trên cạnh BC ( M không trùng với BC ) kẻ đường thẳng song song với AC và AB, chúng cắt AB ở D và AC ở E.

a) ADME là hình gì? Vì sao?

b) Giả sử AD và 3cm, AE = 4cm. Tính độ dài đoạn thẳng AM và diện tích tam giác DME

Cho A, B là hai tập hợp tùy ý. Hãy điền kí hiệu tập hợp thích hợp vào chỗ chấm.

Nếu _{$A \cap B= \varnothing$}  thì _{$A\backslash B=\mathrm{...}$}và _{$B\backslash A=\mathrm{....}$}

Hai xạ thủ độc lập với nhau cùng bắn vào một tấm bia. Mỗi người bắn một viên. Xác suất bắn trúng của xạ thủ thứ nhất là 0,7; của xạ thủ thứ hai là 0,8. Gọi X là số viên đạn bắn trúng bia. Tính kì vọng của X :

Hai xạ thủ A và B cùng bắn vào bia xác suất để xạ thủ bắn trúng là 0,7 và xác suất để xạ thủ b bán kính là 0,8 tính xác suất để có đúng một xạ thủ bắn trúng bia

Hội khỏe Phù Đổng của trường Trần Phú, lớp 10A có 45 học sinh, trong đó có 25 học sinh thi điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu?

Trong hội khỏe Phù Đổng của trường THPT Thanh Miện, lớp 10Acó 45 học sinh, trong đó có 25 học sinh thiđiền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 học sinhkhông tham gia môn nào, 5 học sinhtham gia cả 3 môn. Hỏi số họcsinhtham gia chỉ một môn trong ba môn trên là bao nhiêu?

Cho tam giác ABC nhọn có đường cao AH. Gọi M và N là hình chiếu của H lên AB và AC. CMR: AB . AM = AC . AN

Tìm hệ số của x⁶ trong khai triển ${(\frac{1}{x}+x^3)}^{3n+1}$ với $x\ne 0,$, biết n là số nguyên dương thỏa mãn điều kiện _{${\text{3C}}_{\text{n\hspace{0.05em}+1}}^{\text{2}}{\text{+nP}}_{\text{2}}{\text{=4A}}_{\text{n}}^{\text{2}}$}