20 câu Trắc nghiệm Toán 12 Kết nối tri thức Bài 3. Đường tiệm cận của đồ thị hàm số có đáp án
20 câu hỏi
I. Nhận biết
Cho hàm số y = f(x) có đồ thị như hình vẽ
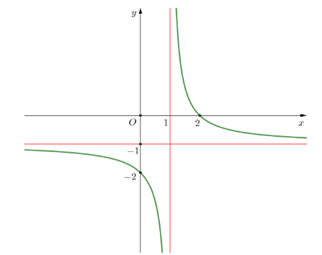
Đồ thị hàm số đã cho có tiệm cận đứng bằng
x = 1.
x = −1.
x = 0.
y = −1.
Cho hàm số \(y = \frac{{x + 1}}{{x - 2}}\). Khẳng định nào sau đây đúng?
Đồ thị hàm số có hai đường tiệm cận.
Hàm số nghịch biến trên \(\mathbb{R}\backslash \left\{ 2 \right\}\).
Hàm số có một cực trị.
Giao điểm của đồ thị và trục tung là \(\left( { - 1\,;\,0} \right)\)
Cho hàm số \(y = \frac{{2x + 1}}{{x - 2}}\). Khẳng định nào dưới đây là đúng?
Hàm số có cực trị.
Đồ thị hàm số có tiệm cận đứng là \(x = 2\).
Đồ thị hàm số đi qua điểm \(A\left( {1;3} \right)\).
Hàm số nghịch biến trên \(\left( { - \infty ;2} \right) \cup \left( {2; + \infty } \right)\).
Cho hàm số y = f(x) có đồ thị như hình vẽ
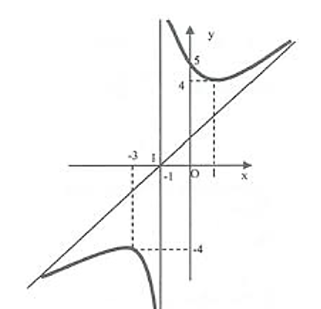
Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
4.
2.
1.
3.
Đồ thị hàm số \(y = \frac{{2x - 1}}{{x + 3}}\) có một đường tiệm cận ngang là
\(x = 3\).
\(y = 2\).
\(x = - 3\).
\(y = - 2\).
II. Thông hiểu
Đồ thị hàm số \(y = \frac{{2x - 1}}{{x - 3}}\) có bao nhiêu đường tiệm cận?
\(0.\)
\(1.\)
\(2.\)
\(3.\)
Viết phương trình các đường tiệm cận của đồ thị hàm số \(y = \frac{{x + 3}}{{2 - x}}\) ?
\(x = 2\) và \(y = - 1\).
\(x = - 1\) và \(y = 2\).
\(x = 2\) và \(y = \frac{1}{2}\).
\(x = - 1\) và \(y = \frac{1}{2}\).
Đường thẳng y = −1 là tiệm cận của đồ thị hàm số nào dưới đây?
\(y = \frac{{x + 3}}{{2 - x}}\).
\(y = \frac{1}{{x + 1}}\) .
\(y = \frac{{ - 2x + 1}}{{2 + x}}\) .
\(y = \frac{{ - {x^2} + 3}}{{x - 1}}\) .
Đường thẳng \(x = - 1\) không là tiệm cận của đồ thị hàm số nào dưới đây?
\(y = \frac{{x + 2}}{{\left| x \right| - 1}}.\)
\(y = \frac{1}{{{x^3} + 1}}.\)
\(y = \frac{{ - {x^2} + x + 2}}{{x + 1}}.\)
\(y = \frac{2}{{{x^2} + 3x + 2}}.\)
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) có bảng biến thiên như hình bên.
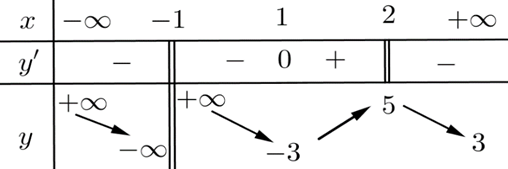
Số tiệm cận của đồ thị hàm số đã cho là.
\(1.\)
\(2.\)
\(3.\)
\(4.\)
Cho hàm số y = f(x) có bảng biến thiên như sau:
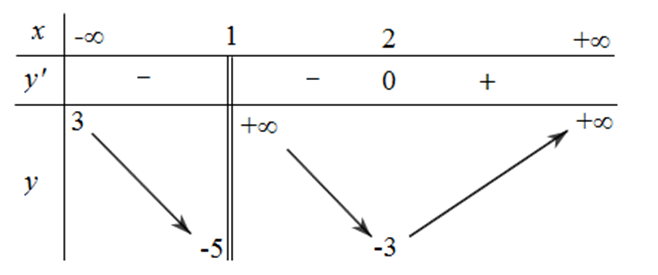
Số các đường tiệm cận (tiệm cận đứng và tiệm cận ngang) của đồ thị hàm số đã cho bằng
\(3\).
\(2\).
\(4\).
\(1\).
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau
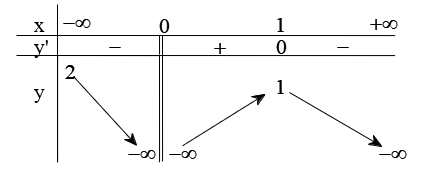
Tổng số đường tiệm cận của đồ thị hàm số \[y = f\left( x \right)\]là
\[1\].
\[0\].
\[3\].
\[2\].
Cho hàm số y = f(x) có đồ thị như hình vẽ dưới đây. Phương trình đường tiệm cận xiên của đồ thị hàm số là
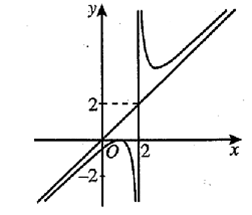
y = x.
y = −x.
y = x + 2.
y = 2x.
Đường tiệm cận xiên của đồ thị hàm số \(y = 2x - 1 + \frac{3}{{x + 1}}\) là
y = 2x.
y = x + 1.
y = 2x − 1.
y = 1 − 2x.
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 2x + 3}}{{x + 1}}\) là
y = x.
y = x + 1.
y = x − 1.
y = 1 − 2x.
III. Vận dụng
Đồ thị hàm số nào dưới đây có đường tiệm cận ngang qua điểm \(A\left( {2;3} \right)\)
\(y = \frac{{x + 3}}{{3x + 2}}\).
\(y = \frac{{2x + 1}}{{x - 2}}\).
\(y = \frac{{3x + 1}}{{2x - 2}}\).
\(y = \frac{{3x + 2}}{{x + 3}}\).
Tìm tọa độ giao điểm hai đường tiệm cận của đồ thị hàm số \[y = \frac{{3 - x}}{{2x + 5}}\]
\(\left( { - \frac{1}{2};\, - \frac{5}{2}} \right).\)
\(\left( { - \frac{5}{2};\,\frac{3}{2}} \right).\)
\(\left( { - \frac{5}{2};\, - \frac{1}{2}} \right).\)
\(\left( { - \frac{1}{2};\,\frac{5}{2}} \right).\)
Cho hàm số y = f(x) có bảng biến thiên
![Cho hàm số y = f(x) có bảng biến thiên Có bao nhiêu giá trị nguyên của m ∈ [−4; 4] để đồ thị hàm số có 4 tiệm cận. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid0-1728824782.png)
Có bao nhiêu giá trị nguyên của m ∈ [−4; 4] để đồ thị hàm số có 4 tiệm cận.
5.
6.
7.
8.
Tiệm cận đứng của đồ thị hàm số \(y = \frac{x}{{{x^2} - 4x}}\) là
\(x = 0.\)
\(x = - 4.\)
\(x = 0\); \(x = 4.\)
\(x = 4.\)
Cho đồ thị hàm số y = f(x) có bảng biến thiên xác định như hình. Biết rằng đồ thị hàm số có tiệm cận đứng x = x0, tiệm cận ngang y = y0 và x0y0 = 16. Tìm m.
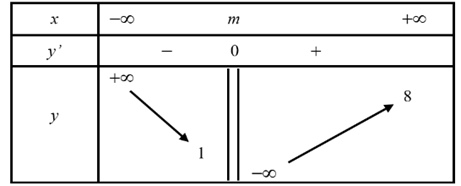
m = 8.
m = −16.
m = 1.
m = 2.