Đề kiểm tra Đường tiệm cận của đồ thị hàm số (có lời giải) - Đề 3
24 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 24. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right) = \frac{{x - 2}}{{x + 1}}\) là:
\(x = - 1\).
\(x = 1\).
\(x = - 2\).
\(x = - 2\).
Tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x + 3}}{{x - 1}}\) là:
\(y = 1\).
\(y = 2\).
\(y = - 3\).
\(y = - 2\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Khi đó hàm số \(y = f\left( x \right)\) là hàm số nào trong các hàm số sau? 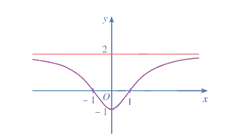
\(y = {\log _3}x\).
\(y = {e^x}\).
\(y = \frac{{2{x^2} - x + 3}}{{x + 1}}\).
\(y = \frac{{2{x^2} - 2}}{{{x^2} + 2}}\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Khi đó hàm số \(y = f\left( x \right)\) là hàm số nào trong các hàm số sau?
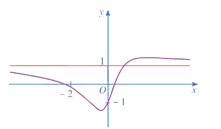
\(y = \frac{{{x^2} - x + 7}}{{{x^2} - 4}}\).
\(y = \frac{{2{x^2} - x + 3}}{{x + 5}}\).
\(y = \frac{{{x^2} + 2x - 1}}{{{x^2} + 1}}\).
\(y = \frac{{x + 4}}{{x - 3}}\).
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{5x - 3}}{{2 - x}}\) là đường thẳng có phương trình:
\(y = \frac{5}{2}.\)
\(y = - 5.\)
\(x = - 5.\)
\(x = 2.\)
Tìm tất cả các giá trị thực của tham số \[m\] để đồ thị hàm số \[y = \frac{{mx - 8}}{{x + 2}}\]có hai đường tiệm cận.
\[m \ne 4.\].
\[m \ne - 4.\].
\[m = 4.\].
\[m = - 4.\].
Cho hàm số \[y = \frac{{2x - 1}}{{x + 2}},\] tổng số đường tiệm cận của đồ thị hàm số là
\[1\].
\[2\].
\[3\].
\[0\].
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\,\left( {ad - bc \ne 0;ac \ne 0} \right)\) có đồ thị như hình vẽ bên dưới. Tìm phương trình đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số.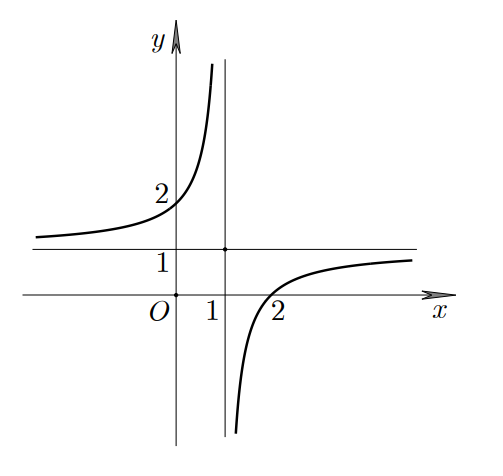
\(x = 1,\,y = 1\).
\(x = - 1,\,y = 1\).
\(x = 1,\,y = 2\).
\(x = 2,\,y = 1\).
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{x + 3}}{{2x - 2}}\)
\(x = 1\).
\(x = 2\).
\(x = \frac{1}{2}\).
\(x = - 3\).
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{2x + 5}}{{2x + 4}}\)
\(x = - 2\).
\(x = 1\).
\(x = \frac{1}{2}\).
\(x = - \frac{5}{2}\).
Cho đồ thị hàm số có hình vẽ như dưới, đường thẳng tiệm cận ngang của đồ thị hàm số là đường có nét đứt. Hỏi đó là đồ thị của hàm số nào trong các hàm số sau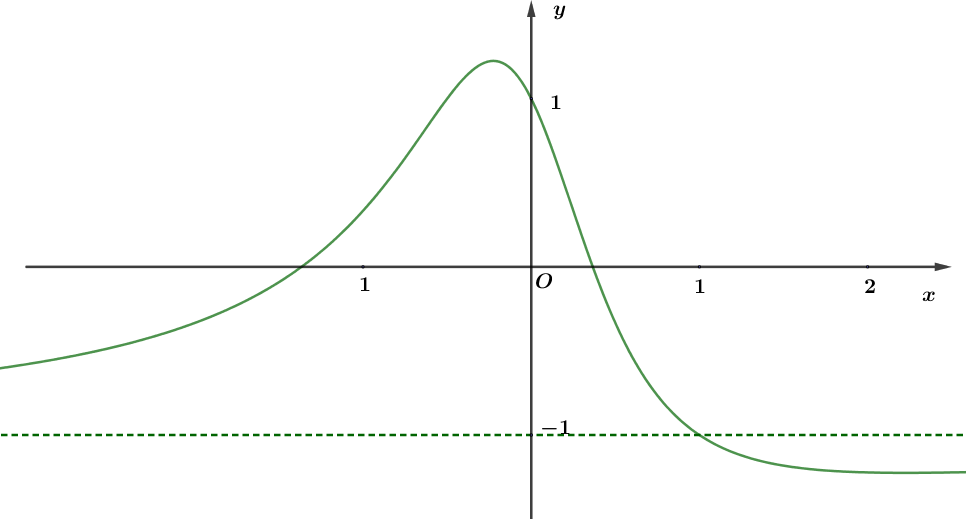
\(y = \frac{{2{x^2} + 2x - 1}}{{x + 1}}\).
\(y = \frac{{2{x^2} + 2x - 1}}{{ - 2{x^2} - 1}}\).
\(y = \frac{{2{x^2} + 2x - 1}}{{x - 1}}\).
\(y = \frac{{2{x^2} + 2x - 1}}{{ - 2{x^2} + 1}}\).
Cho đồ thị hàm số có hình vẽ như dưới, đường thẳng tiệm cận ngang của đồ thị hàm số là đường có nét đứt. Hỏi đó là đồ thị của hàm số nào trong các hàm số sau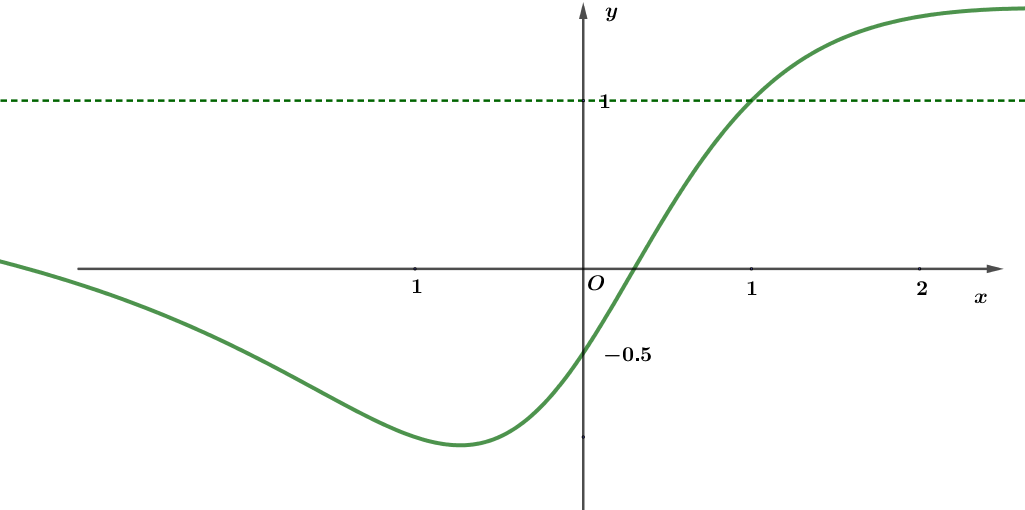
\(y = \frac{{{x^2} + 2x - 1}}{{x + 1}}\).
\(y = \frac{{{x^2} + 3x - 1}}{{{x^2} + 2}}\).
\(y = \frac{{2{x^2} + 2x - 1}}{{2{x^2} - 1}}\).
\(y = \frac{{2{x^2} + 2x - 1}}{{2{x^2} + 1}}\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau
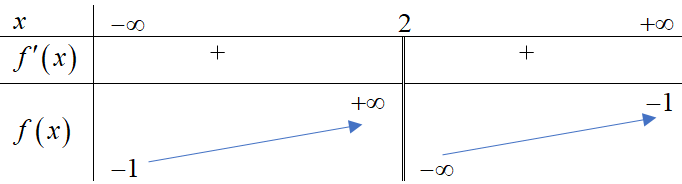
a) Đồ thị hàm số có đường tiệm cận đứng là \[x = 2\]
b) Đồ thị hàm số có đường tiệm cận ngang là \[x = - 1\]
c) Tổng số đường tiệm cận của đồ thị hàm số đã cho là \[2\]
d) Hàm số đồng biến trên \[\mathbb{R}\]
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau
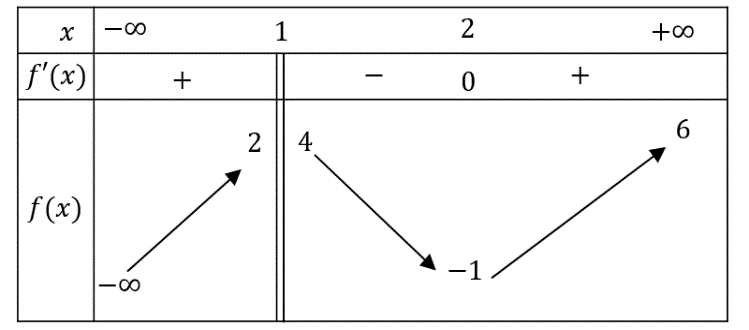
a) Đồ thị hàm số có đường tiệm cận đứng là \[x = 1\]
b) Đồ thị hàm số có đường tiệm cận ngang là \[y = 6\]
c) Tổng số đường tiệm cận của đồ thị hàm số đã cho là \[2\]
d) Tổng số tiệm cận ngang của đồ thị hàm số \[y = \frac{1}{{f(x) + 2}}\] là \[1\]
Cho hàm số \[y = f\left( x \right)\] xác định và có đạo hàm trên \[\mathbb{R}\backslash \left\{ { \pm 2} \right\}\]. Hàm số \[f\left( x \right)\] có bảng biến thiên như hình vẽ dưới đây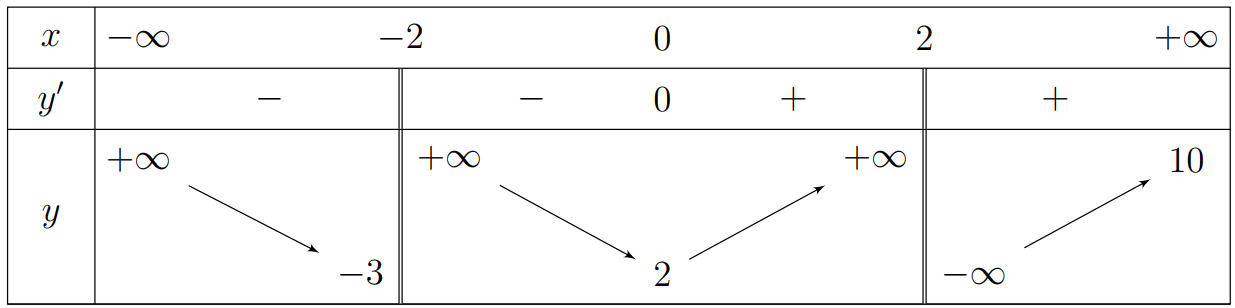
Xét tính đúng – sai của các phát biểu sau:
a) Đường tiệm cận ngang của đồ thị hàm số \[y = f\left( x \right)\]là đường thẳng \(y = 10\).
b) Một đường tiệm cận đứng của đồ thị hàm số \[y = f\left( x \right)\]là đường thẳng \(x = - 3\).
c) Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \[y = f\left( x \right)\]là 3.
d) Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \[y = \frac{1}{{2f\left( x \right) + 6}}\] là 4.
Cho đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - \left( {2m + 1} \right)x + {m^2} - 3}}\] với tham số \[m\]. Xét tính đúng – sai của các phát biểu sau:
a) Với mọi \(m\) đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - \left( {2m + 1} \right)x + {m^2} - 3}}\] không tiệm cận đứng và tiệm cận ngang.
b) Đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - \left( {2m + 1} \right)x + {m^2} - 3}}\] có 1 tiệm cận ngang là \[y = 0\].
c) Với \(m = - 1\) thì đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - \left( {2m + 1} \right)x + {m^2} - 3}}\] có \(2\) đường tiệm cận đứng.
d) Có ba giá trị của \(m\) đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - \left( {2m + 1} \right)x + {m^2} - 3}}\] có đúng hai đường tiệm cận.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn.
Có bao nhiêu giá trị nguyên của\[m \in \left[ { - 2025;2025} \right]\] để đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} + 2\left( {m - 1} \right)x + {m^2} - 2}}\] có đúng hai đường tiệm cận đứng?
Cho hàm số bậc ba \[y = f\left( x \right)\] có đạo hàm liên tục trên \[\mathbb{R}\]. Đồ thị hàm \[y = f\left( x \right)\] có dạng như hình vẽ bên dưới. Hỏi đồ thị hàm số \[g\left( x \right) = \frac{{{x^2} - 1}}{{{f^2}\left( x \right) - 4f\left( x \right)}}\] có bao nhiêu đường tiệm cận đứng?![Câu 18: Cho hàm số bậc ba \[y = f\left( x \right)\] có đạo hàm liên tục trên \[\mathbb{R}\]. Đồ thị hàm \[y = f\left( x \ri (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/9-1759194921.png)
Cho hàm số \(f\left( x \right) = \frac{{ax + b}}{{cx + d}}(a \ne 0;c \ne 0;ad - bc \ne 0)\) có đồ thị như hình vẽ dưới đây.
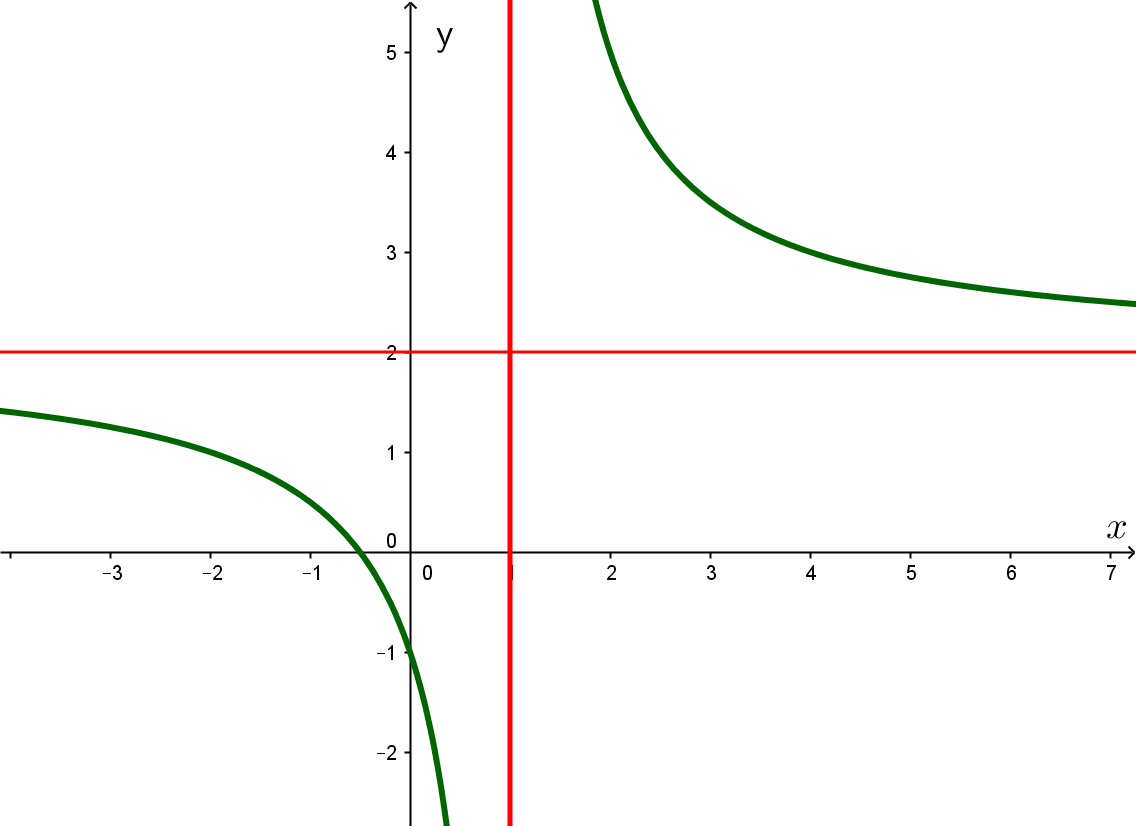
Đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) có tổng số bao nhiêu đường tiệm cận?
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ dưới đây.
![Đồ thị hàm số \[y = \left| {f\left( x \right)} \right|\] có 2 tiệm cận ngang là hai đường thẳng \[y = m\] và \[y = n\]. Tính \(m + n\)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/12-1759195052.png)
Đồ thị hàm số \[y = \left| {f\left( x \right)} \right|\] có 2 tiệm cận ngang là hai đường thẳng \[y = m\] và \[y = n\]. Tính \(m + n\)?
Số đường tiệm cận của đồ thị hàm số \(y = \frac{{{x^2} - 3x + 2}}{{4 - {x^2}}}\)là bao nhiêu?
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau:
![Câu 22: Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau: Đồ thị hàm số\[g\left( x \right){\rm{ }} = \frac{2}{{3f\left( x \right) - 2}}\] có tất cả bao nhiêu đường tiệm cận? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/14-1759195115.png)
Đồ thị hàm số\[g\left( x \right){\rm{ }} = \frac{2}{{3f\left( x \right) - 2}}\] có tất cả bao nhiêu đường tiệm cận?
Số đường tiệm cận đứng của đồ thị hàm số \(y = \frac{{\left( {{x^2} - 3x + 2} \right)\sin x}}{{{x^3} - 4x}}\) là bao nhiêu?
Cho hàm số \[y = f(x)\]có bảng biến thiên như sau:
![Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \[y = \frac{2}{{3f(x) - 2}}\]là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/15-1759195174.png)
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \[y = \frac{2}{{3f(x) - 2}}\]là