12 bài tập Một số bài toán về đường tiệm cận của đồ thị hàm số có chứa tham số có lời giải
12 câu hỏi
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số \[y = \frac{{mx - 8}}{{x + 2}}\] có hai đường tiệm cận.
m ≠ 4;
m ≠ −4;
m = 4;
m = −4.
Cho hàm số \(y = \frac{{ax + 1}}{{bx - 2}}.\) Tìm a, b để đồ thị hàm số có x = 1 là tiệm cận đứng và \(y = \frac{1}{2}\) là tiệm cận ngang.
a = −1; b = 2;
a = 4; b = 4;
a = 1; b = 2;
a = −1; b = −2.
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số \(y = \frac{{{x^2} + m}}{{{x^2} - 3x + 2}}\) có đúng hai đường tiệm cận.
m = −1;
m ∈ {1; 4};
m = 4;
m ∈ {−1; −4}.
Tìm tất cả giá trị của tham số m để đường tiệm cận xiên của đồ thị hàm số \(y = 2mx + 3 - \frac{4}{{x + 1}}\) đi qua điểm M(1; 7).
m = 1;
m = 3;
m = 2;
m = −2.
Biết rằng đồ thị của hàm số \(y = \frac{{\left( {n - 3} \right)x + n - 2017}}{{x + m + 3}}\) (m, n là các số thực) nhận trục hoành làm tiệm cận ngang và trục tung là tiệm cận đứng. Tính tổng m + n.
0;
−3;
3;
6.
Có bao nhiêu giá trị nguyên dương của tham số m để đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - 8x + m}}\] có 3 đường tiệm cận?
14;
8;
15;
16.
Cho đồ thị hàm số y = f(x) có bảng biến thiên xác định như hình. Biết rằng đồ thị hàm số có tiệm cận đứng x = x0, tiệm cận ngang là y = y0 và x0y0 = 16. Hỏi m bằng?
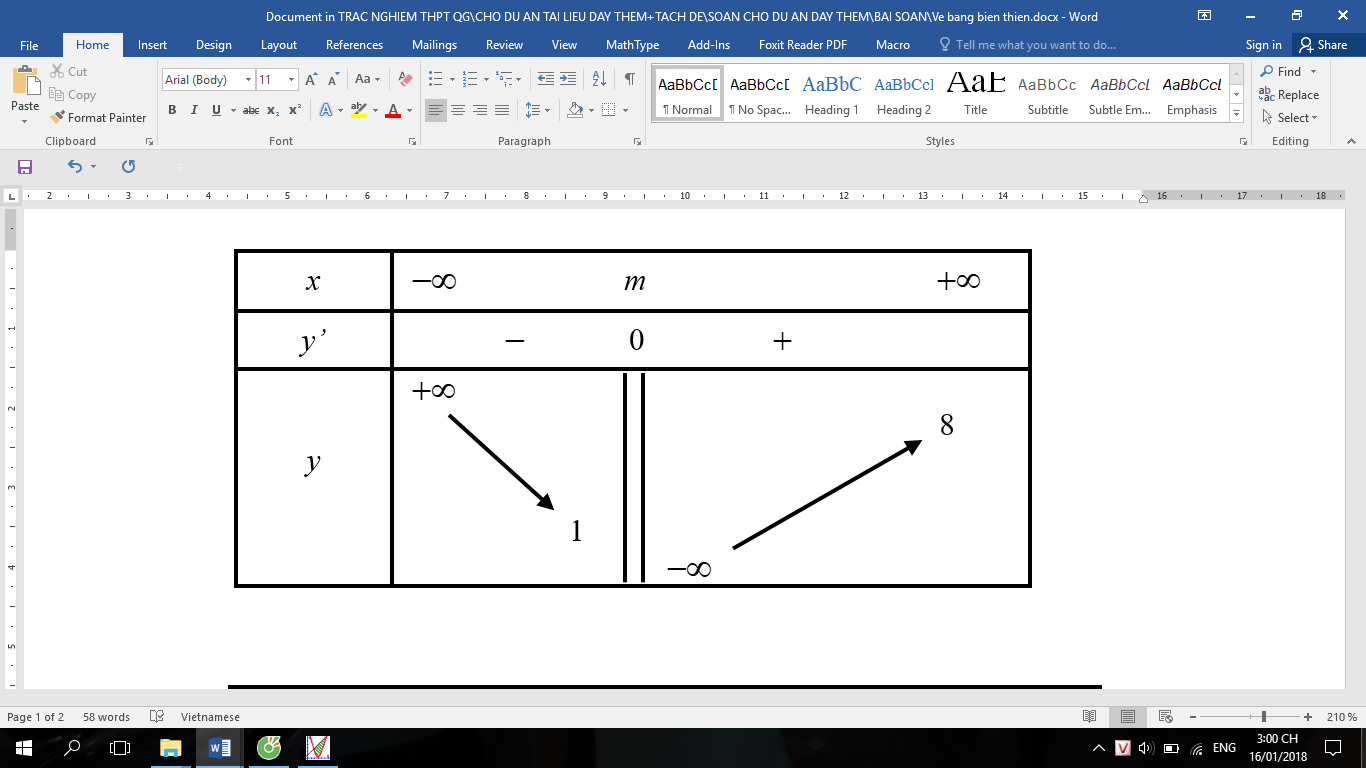
m = 8;
m = −16;
m = 1;
m = 2.
Cho hàm số y = f(x) có bảng biến thiên:
![Cho hàm số y = f(x) có bảng biến thiên: Có bao nhiêu giá trị nguyên của m ∈ [−4; 4] để hàm số có 4 tiệm cận? (ảnh 1)](https://video.vietjack.com/upload2/images/1742397066/1742397854-image3.png)
Có bao nhiêu giá trị nguyên của m ∈ [−4; 4] để hàm số có 4 tiệm cận?
5;
6;
7;
8.
Cho hàm số y = f(x) có bảng biến thiên sau:

Tìm tổng số các giá trị nguyên dương của tham số m ∈ (−10; 10) để đồ thị hàm số y = f(x) có tổng số đường tiệm cận đứng và đường tiệm cận ngang là 4.
42;
45;
−3;
0.
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ. Định tham số m để giao điểm của đường tiệm cận đứng và tiệm cận ngang là điểm I(−1; 1).
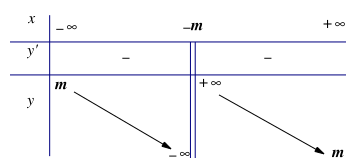
Không có m;
m = 0;
m = −1;
m = 1.
Tìm điều kiện của tham số m để đồ thị của hàm số \(y = \frac{{\left( {2m + 1} \right)x + 3}}{{x + 1}}\) có đường tiệm cận ngang đi qua điểm A(−2; 7).
Cho hàm số \[y = f\left( x \right) = \frac{{nx + 1}}{{x + m}}\]; (mn ≠ 1)xác định trên ℝ\{−1}, liên tục trên từng khoảng xác định và có đồ thị như hình vẽ:
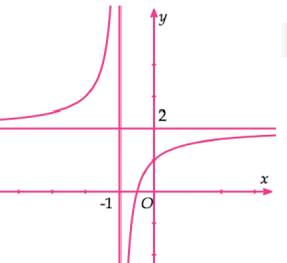
Tính tổng m + n.