Đề kiểm tra Đường tiệm cận của đồ thị hàm số (có lời giải) - Đề 4
22 câu hỏi
Cho hàm số \(y = \frac{{2{x^2} - 3x - 3}}{{x - 2}}\). Tiệm cận xiên của đồ thị hàm số là đường thẳng
\(y = 2x - 1\).
\(y = 2x + 1\).
\(y = 2x - 3\).
\(y = 2x + 3\).
Xác định toạ độ giao điểm của đường tiệm cận đứng và đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{2{x^2} - 3x + 2}}{{x - 1}}\)
(1;2).
\(\left( {1;\,1} \right)\).
\(\left( {1;\, - 1} \right)\).
\(\left( {1;\,0} \right)\).
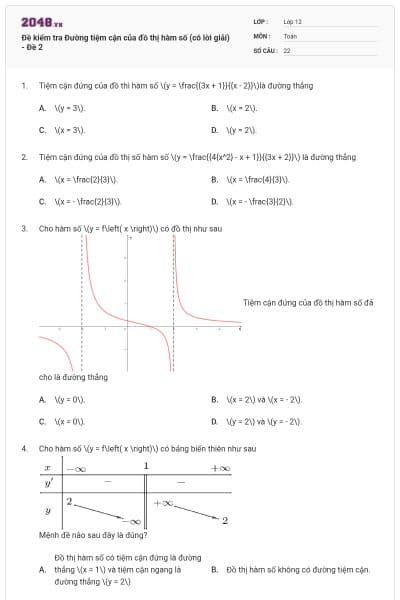
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau :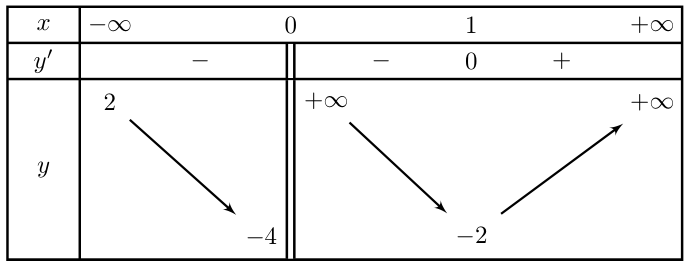
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
\[1\].
\[3\].
\[4\].
\[2\].
Số tiệm cận đứng của đồ thị hàm số\(y = \frac{{\sqrt {x + 9} - 3}}{{{x^2} + x}}\) là
\[3\].
\[2\].
\[0\].
\(1\).
Phương trình đường tiệm cận ngang của đồ thị hàm số \[y = \frac{{2x + 1}}{{x - 1}}\] là
\[x = 2\].
\[y = 2\].
\[x = 1\].
\[y = 1\].
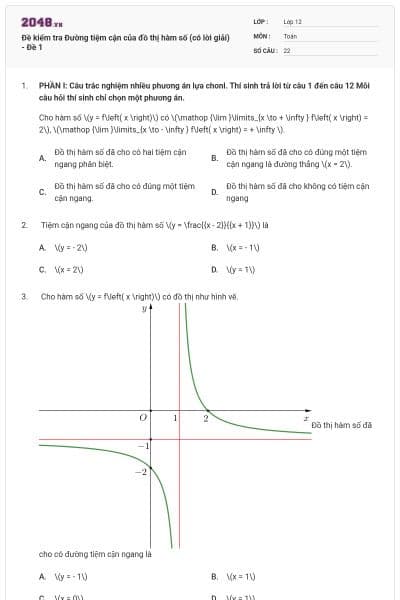
Cho hàm số \(y = f(x)\) có đồ thị như hình vẽ bên. Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số lần lượt là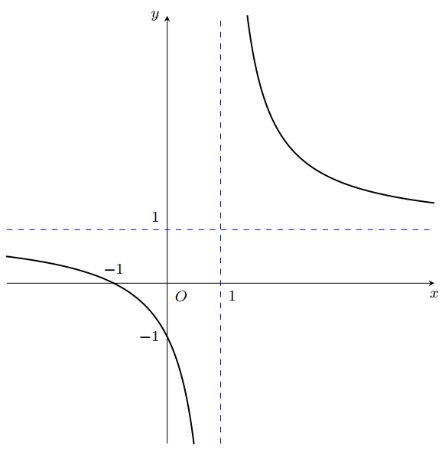
\(x = - 1;y = 1\).
\(x = 1;y = - 1\).
\(x = - 1;y = - 1\).
\(x = 1;y = 1\).
Phương trình đường tiệm cận xiên của đồ thị hàm số \[y = \frac{{{x^2} - x + 1}}{{x + 1}}\] là
\[y = x + 2\].
\[y = x - 2\].
\[y = x + 1\].
\[y = x - 1\].
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ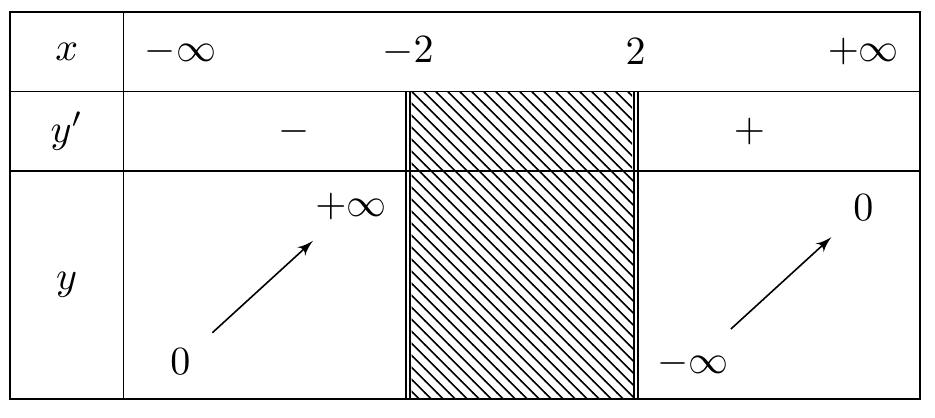
Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số bằng
\(3\).
\(4\).
\(1\).
\(2\).
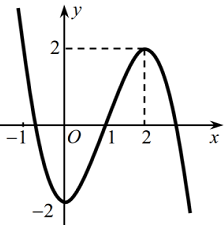
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Tìm khẳng định đúng trong các khẳng định sau? 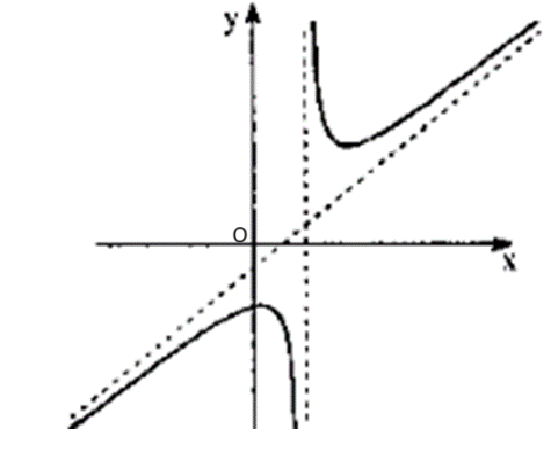
Đồ thị hàm số \(y = f\left( x \right)\)có một tiệm cận đứng và một tiệm cận ngang .
Đồ thị hàm số \(y = f\left( x \right)\)có một tiệm cận xiên và một tiệm cận ngang.
Đồ thị hàm số \(y = f\left( x \right)\)có một tiệm cận đứng và một tiệm cận xiên.
Đồ thị hàm số \(y = f\left( x \right)\)có hai tiệm cận xiên.
Đồ thị hàm số nào sau đây có tiệm cận xiên:
\(y = {x^2} - 2x\).
\(y = x + 1\).
\(y = \frac{x}{{x + 2}}\).
\(y = \frac{{{x^2}}}{{x + 1}}\).
Tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 3x + 5}}{{x + 2}}\) là
\(y = x\).
\(y = x + 1\).
\(y = x + 2\).
\(y = x + 3\).
Số tiệm cận xiên của đồ thị hàm số \(y = \sqrt {4{x^2} - x + 3} \) là
2.
3.
0.
1.
Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên như hình vẽ dưới đây
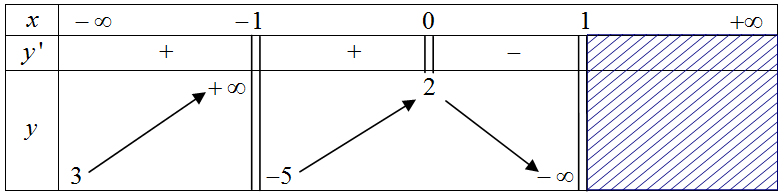
Xét tính đúng sai các mệnh đề sau:
\(x = 1,x = - 1\) là đường tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\) .
\(x = 0\) là đường tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\) .
\(y = 3;y = 1\) là các đường tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\) .
Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số \(y = f\left( x \right)\) là 3.
Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}\backslash \left\{ 1 \right\}\] và có bảng biến thiên như sau
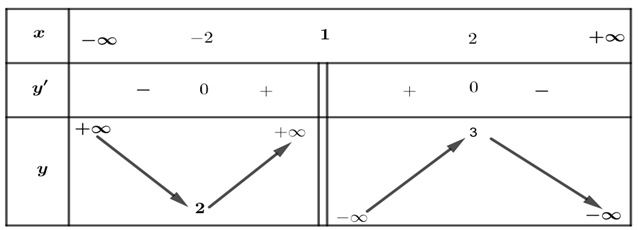
Xét hàm số \(y = g\left( x \right) = f\left( {{x^2} - 2x - 2} \right)\). Xét tính đúng/sai của các mệnh đề sau:
a) Hàm số \(y = g\left( x \right)\) có tập xác định là \[D = \mathbb{R}\backslash \left\{ {1 \pm \sqrt 3 } \right\}.\]
b) Hàm số \(y = g\left( x \right)\) có 2 tiện cận đứng.
c) Hàm số \(y = g\left( x \right)\) có 1 tiệm cận ngang là \(y = 1\).
d) Tổng số đường tiệm cận của đồ thị hàm số \(y = g\left( x \right)\) là 3.
Cho hàm số \(y = \frac{{m{x^2} + \left( {3{m^2} - 2} \right)x - 2}}{{x + 3m}}\)\(\left( 1 \right)\), với \(m\)là tham số. Các mệnh đề sau đúng hay sai?
a. Khi \(m = 1\) thì đồ thị hàm số của \(\left( 1 \right)\) không có tiệm cận ngang.
b. Khi \(m = 1\) thì đồ thị hàm số của \(\left( 1 \right)\) có tiệm cận đứng là \(y = - 3\).
c. Khi \(m = 1\) thì đồ thị hàm số của \(\left( 1 \right)\) có tiệm cận xiên là \(y = x - 2\).
d. Khi góc giữa hai đường tiệm cận của đồ thị hàm số bằng 450 thì \(m = 2\).
Gọi \(\left( C \right)\) là đồ thị của hàm số \(y = \frac{{m{x^2} + \left( {3 - m} \right)x + {m^2} - 2}}{{x - 1}}\), với \(m\)là tham số. Gọi \(\left( d \right)\) là đường tiệm cận xiên của \(\left( C \right)\). Các mệnh đề sau đúng hay sai?
a. Khi \(m = 2\) thì \(\left( d \right)\) có phương trình là \(y = 2x + 3\).
b. Khi \(m = 1\) thì \(\left( d \right)\) đi qua \(A\left( {1;\,4} \right)\) .
c. Có 2 đường thẳng \(\left( d \right)\) tạo với hai trục tọa độ một tam giác có diện tích bằng 9.
d. Khoảng cách từ gốc tọa độ \(O\) đến \(\left( d \right)\) bằng \(\sqrt 3 \) thì \(m = \sqrt 5 \).
Có bao nhiêu giá trị nguyên dương của tham số \(m\)để đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - 8x + m}}\]có 3 đường tiệm cận?
Cho hàm số bậc ba \(y = f(x)\) có đồ thị như hình vẽ bên. Tìm số đường cận đứng của đồ thị hàm số \(y = g(x) = \frac{{(x + 1)({x^2} - 1)}}{{{f^2}(x) - 2f(x)}}\).
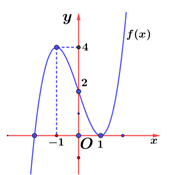
Cho \(f\left( x \right)\) là hàm đa thức bậc ba và có đồ thị như hình vẽ bên dưới.
Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 100;100} \right]\)để đồ thị hàm số \(y = \frac{{\sqrt {1 + m{x^2}} }}{{f(x) - m}}\)có đúng hai đường tiệm cận?
Cho hàm số \[y = \frac{{10 + \sqrt {6x - {x^2}} }}{{\sqrt {{x^2} - 4x + 2m} }}\]có đồ thị \[\left( {{C_m}} \right)\]. Tìm số giá trị nguyên của tham số \[m\] để \[\left( {{C_m}} \right)\]có đúng hai tiệm cận đứng.
Người ta thống kê được chi phí sửa chữa, vận hành máy móc trong một năm của một xưởng sản xuất được tính bởi công thức \(f\left( x \right) = \frac{{2000x - 1500}}{{35x + 5}}\)(triệu đồng). Biết \(x\) là số năm kể từ lúc máy móc vận hành lần đầu tiên, số năm càng nhiều thì chi phí càng cao. Khi số năm \(x\) đủ lớn thì chi phí vận hành máy móc trong một năm gần với số nào? (làm tròn đến 1 chữ số thập phân sau dấu phẩy).
Để thiết kế một bể cá hình hộp chữ nhật có chiều cao là \(80\) cm, thể tích là \[12800\] cm3. Người thợ dùng loại kính để sử dụng làm mặt bên có giá thành \[70000\] VNĐ/m2 và loại kính đề làm mặt đáy có giá thành \[100000\] VNĐ/m2. Gọi\[x\]là chiều dài của đáy bể cá với\[\left( {x > 0,\,\,x\,(m)} \right)\];\[f\left( x \right)\]là hàm số xác định chi phí để hoàn thành bể cá. Xác định các đường tiệm cận của đồ thị hàm số\[f\left( x \right)\].......................