Đề kiểm tra Đường tiệm cận của đồ thị hàm số (có lời giải) - Đề 1
22 câu hỏi
PHẦN I: Câu trắc nghiệm nhiều phương án lựa chonl. Thí sinh trả lời từ câu 1 đến câu 12 Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \(y = f\left( x \right)\) có \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\), \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = + \infty \).
Đồ thị hàm số đã cho có hai tiệm cận ngang phân biệt.
Đồ thị hàm số đã cho có đúng một tiệm cận ngang là đường thẳng \(x = 2\).
Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
Đồ thị hàm số đã cho không có tiệm cận ngang
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{x - 2}}{{x + 1}}\) là
\(y = - 2\)
\(x = - 1\)
\(x = 2\)
\(y = 1\)
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ.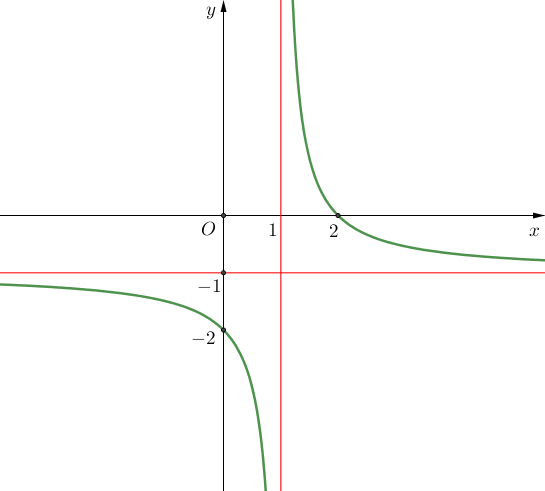 
Đồ thị hàm số đã cho có đường tiệm cận ngang là
\(y = - 1\)
\(x = 1\)
\(x = 0\)
\(y = 1\)
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau: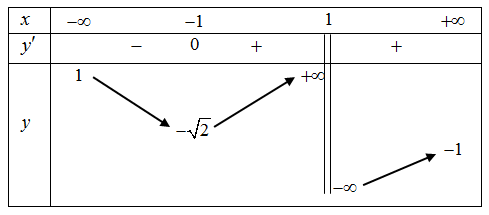
Số đường tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\)
\(1\)
\(4\)
\(2\)
\(3.\)
Cho hàm số \(y = f\left( x \right)\) có \(\mathop {\lim }\limits_{x \to - {2^ + }} f\left( x \right) = + \infty \) và \(\mathop {\lim }\limits_{x \to - {2^ - }} f\left( x \right) = - \infty \)
Đồ thị hàm số đã cho có hai tiệm cận đứng phân biệt.
Đồ thị hàm số đã cho có đúng một tiệm cận ngang là đường thẳng \(y = 2\).
Đồ thị hàm số đã cho có đúng một tiệm cận đứng là đường thẳng \(x = 2\).
Đồ thị hàm số đã cho không có tiệm cận đứng
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{x - 1}}{{x - 3}}\) là
\(x = 3\)
\(x = - 3\)
\(x = - 1\)
\(x = 1\)
Đường tiệm cận đứng của đồ thi hàm số \(y = \frac{{{x^2} + 3x - 1}}{{x + 1}}\)là:
\(x = - 1\).
\(x = 1\).
\(x = 0\).
\(x = 2\).
Cho hàm số \(y = f(x)\)có đồ thị như hình vẽ bên. Tiệm cận đứng của đồ thị là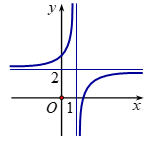
\(x = - 1\).
\(x = 1\).
\(x = 0\).
\(x = 2\).
Đường thẳng \(y = ax + b\) (\(a \ne 0\)) là đường tiệm cận xiên của đồ thị hàm số \(y = f(x)\) nếu:
\(\mathop {\lim }\limits_{x \to a} \left[ {f(x) - (ax + b)} \right] = 0\).
\(\mathop {\lim }\limits_{x \to - \infty } \left[ {f(x) - (ax + b)} \right] = a\).
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\)
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = b\).
Đồ thị hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\) có tiệm cận xiên là đường thẳng:
\(y = x\).
\(y = x - 1\).
\(y = 2x - 1\)
\(y = x + 1\).
Đồ thị hàm số \(y = f(x)\) có tiệm cận xiên là đường thẳng: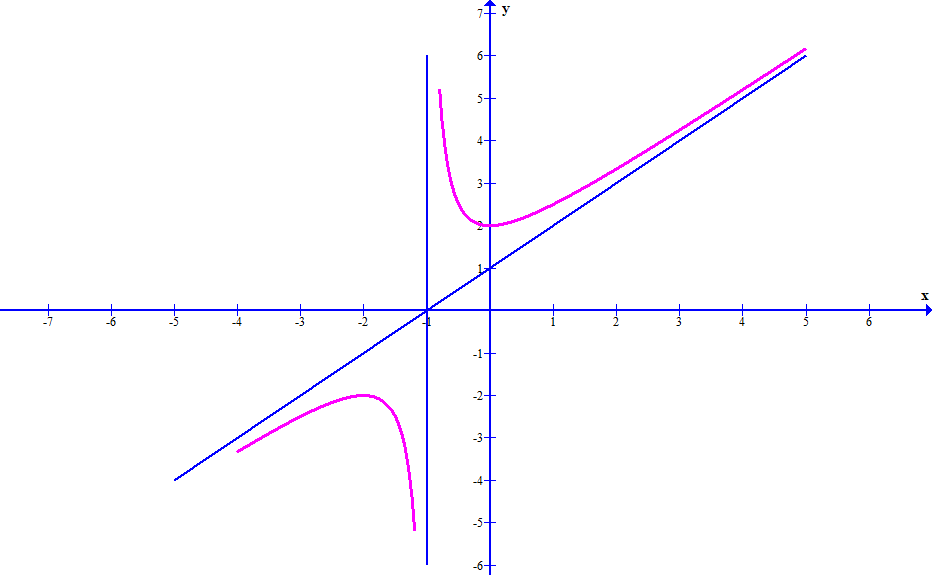
\(y = x\).
\(y = x - 1\).
\(y = 2x - 1\)
\(y = x + 1\).
Đồ thị hàm số \(y = \sqrt {{x^2} + 2x + 2} \) có mấy đường tiệm cận xiên:
\(0\).
\(1\).
\(2\).
\(3\).
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{x - 1}}{{2x - 3}}\) \[\left( C \right)\].
a) Tiệm cận đứng của hàm số là \(x = \frac{3}{2}\).
b) Tọa độ giao điểm hai đường tiệm cận thuộc đường thẳng \(x - y - 1 = 0\)
c) Đường thẳng \(2x + y - 1 = 0\) cắt TCĐ, TCN của hàm số tại các điểm A và B. Diện tích của tam giác IAB bằng \(\frac{{25}}{4}\), với I là giao điểm hai đường tiệm cận.
d) Gọi \(I\) là giao điểm của hai tiệm cận của đồ thị hàm số. Khoảng cách từ \(I\) đến một tiếp tuyến bất kỳ của đồ thị hàm số đã cho đạt giá trị lớn nhất bằng \(\frac{1}{{\sqrt 2 }}\).
Cho hàm số \(y = \frac{{ - {x^2} + 4x + 3 + m}}{{x - 2}}\) \[\left( C \right)\].
a) Khi \(m = 0\), tiệm cận đứng của hàm số là \(x = 2\).
b) Khi \(m = 0\), tọa độ giao điểm của tiệm cận đứng đồ thị và đường thẳng \(x - y - 1 = 0\) thuộc parabol: \(y = {x^2}\)
c) Khi \(m = 0\), lấy \(M\) là điểm bất kỳ trên đồ thị \(\left( C \right)\), gọi \({d_1}\) là khoảng cách từ M đến đường tiệm cận tiệm cận đứng, gọi \({d_2}\) là khoảng cách từ M đến đường thẳng \(y = - x + 2\,\). Tích \({d_1}.{d_2} = 7\)
d) Gọi S là tập hợp các giá trị nguyên dương của m để hàm số không có tiệm cận đứng. Số phần tử của S là 1.
Cho hàm số \(y = \frac{{x - 1}}{{m{x^2} - 2x + 3}}\) \[\left( C \right)\].
a) Khi \(m \ne 0\), hàm số có tiệm cận ngang \(y = 0\).
b) Khi \(m = 0\), tọa độ giao điểm của hai đường tiệm cận thuộc đường thẳng \(x - y - 2 = 0\).
c) Hàm số có 1 tiệm cận đứng khi \(m = 2\)
d) Gọi S là tập hợp các giá trị nguyên âm của \(m \in \left[ { - 5; - 1} \right]\) để hàm số có ba đường tiệm cận. Số phần tử của S là 1.
Cho hàm số \(y = \frac{{{x^2} + x - 2}}{{{x^2} - 2x + m}}\) \[\left( C \right)\].
a) Khi \(m = 0\), hàm số có tiệm cận ngang \(y = 1\).
b) Khi \(m = 0\), hàm số có 3 tiệm cận.
c) Có hai giá trị của m để hàm số có đúng một TCĐ.
d) Gọi S là tập hợp các giá trị nguyên của \(m \in \left[ { - 8;8} \right]\) để hàm số có ba đường tiệm cận. Số phần tử của S là \(7\).
Phần III. Câu hỏi trắc nghiệm trả lời ngắn (Thí sinh trả lời từ câu 01 đến câu 06)
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau
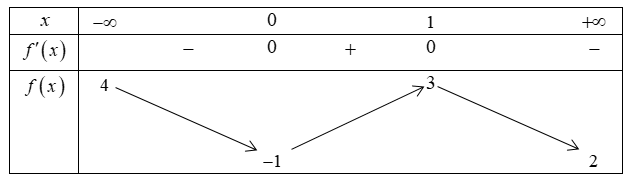
Biết đồ thị hàm số \(g\left( x \right) = f\left( {\sqrt {{x^2} + 2x} - x} \right)\) có hai đường tiệm cận ngang là \(y = a\) và \(y = b\), trong đó \(a < b\). Tính \(S = a - 100b\).
Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất \(x\) (sản phẩm) là \(C\left( x \right) = 150x + 900\) (nghìn đồng). Khi sản xuất càng nhiều sản phẩm thì chi phí sản xuất trung bình cho mỗi sản phẩm không vượt quá \(t\) (nghìn đồng). Tìm giá trị nhỏ nhất của \(t\).
Cho hàm số \[y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\] \[\left( {a \ne 0} \right)\]có đồ thị như hình vẽ bên dưới
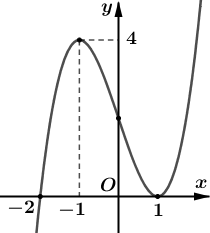
Tìm số đường tiệm cận đứng của đồ thị hàm số \(g\left( x \right) = \frac{{\sqrt x }}{{f\left( {{x^2} - 1} \right) - 4}}\).
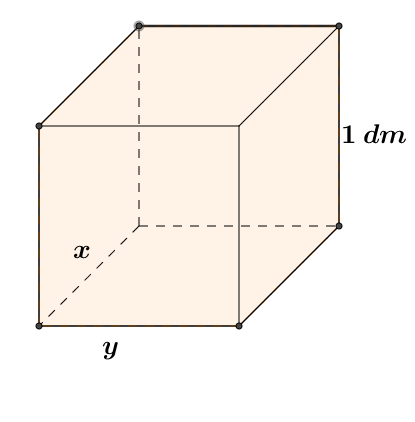
Từ một tấm tôn hình chữ nhật có các kích thước là \(x\,\left( m \right)\), \(y\,\left( m \right)\) với \(x > 2\)và \(y > 2\) và diện tích bằng \(10{m^2}\), người ta cắt bốn hình vuông bằng nhau ở bốn góc rồi gập thành một cái thùng dạng hình hộp chữ nhật không nắp (như hình vẽ) có chiều cao bằng \[1\,m\]. Thể tích của thùng là hàm số \(V\left( x \right)\) trên khoảng \(\left( {2; + \infty } \right)\). Đồ thị hàm số \(y = \frac{1}{{V\left( x \right)}}\) có bao nhiêu đường tiệm cận đứng?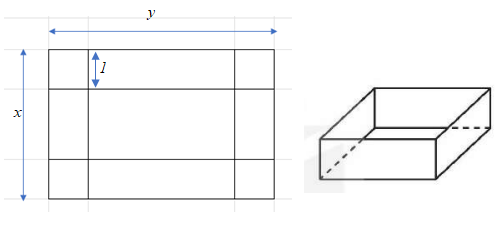
Cho hàm số \(f\left( x \right) = 2x - \sqrt {{x^2} - x} \). Tìm số đường tiệm cận xiên của đồ thị hàm số.
Người ta muốn làm một cái bể dạng hình hộp chữ nhật không nắp (như hình vẽ) có thể tích bằng \(5{m^3}\). Chiều cao của bể là \(10dm\), các kích thước khác là \(x\,\left( m \right)\), \(y\,\left( m \right)\) với \(x > 0\)và \(y > 0\). Diện tích toàn phần của bể (không kể nắp) là hàm số \(S\left( x \right)\) trên khoảng \(\left( {0; + \infty } \right)\). Đường tiệm cận xiên của đồ thị hàm số \(S\left( x \right)\) là đường thẳng \(y = ax + b\). Tính giá trị của biểu thức \(P = {a^2} + {b^2}\).
