Đề kiểm tra Đường tiệm cận của đồ thị hàm số (có lời giải) - Đề 2
22 câu hỏi
Tiệm cận đứng của đồ thì hàm số \(y = \frac{{3x + 1}}{{x - 2}}\)là đường thẳng
\(y = 3\).
\(x = 2\).
\(x = 3\).
\(y = 2\).
Tiệm cận đứng của đồ thị số hàm số \(y = \frac{{4{x^2} - x + 1}}{{3x + 2}}\) là đường thẳng
\(x = \frac{2}{3}\).
\(x = \frac{4}{3}\).
\(x = - \frac{2}{3}\).
\(x = - \frac{3}{2}\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như sau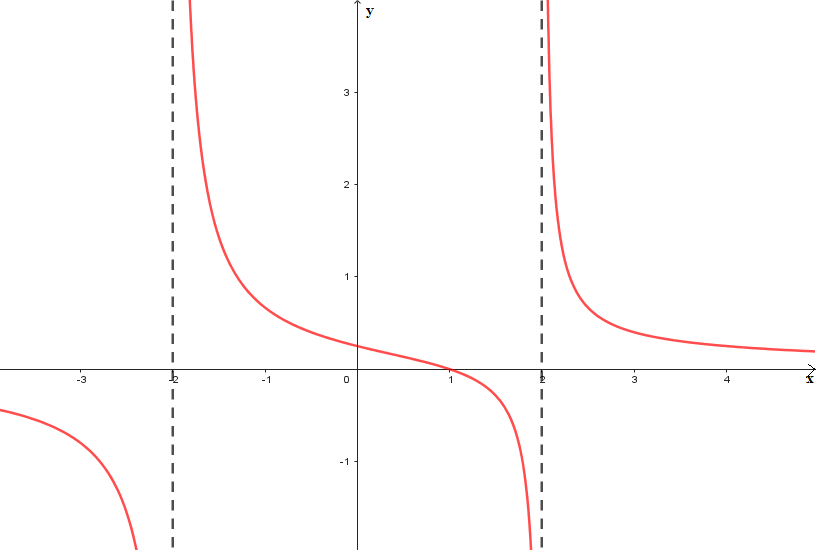 
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng
\(y = 0\).
\(x = 2\) và \(x = - 2\).
\(x = 0\).
\(y = 2\) và \(y = - 2\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau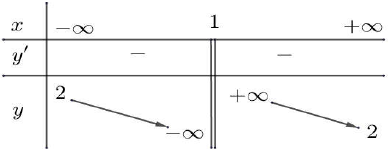
Mệnh đề nào sau đây là đúng?
Đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = 1\) và tiệm cận ngang là đường thẳng \(y = 2\)
Đồ thị hàm số không có đường tiệm cận.
Đồ thị hàm số chỉ có một đường tiệm cận.
Đồ thị hàm số có tiệm cận ngang là đường thẳng \(x = 1\) và tiệm cận đứng là đường thẳng \(y = 2\).
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{3 - 2x}}{{x + 1}}\) là
\[x = - 2\].
\[y = - 2\].
\[y = - 1\].
\[x = - 1\].
Cho hàm số \(f(x)\) có bảng biến thiên như sau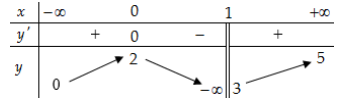
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
\[3\].
\[1\].
\[2\].
\[4\].
Cho hàm số \(f(x)\) có đồ thị như hình vẽ bên dưới.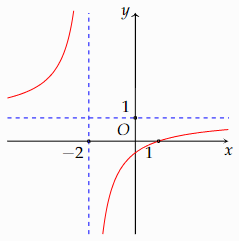
Đường tiệm cận ngang của đồ thị hàm số là
\(x = 1\).
\(y = - 2\).
\(x = - 2\).
\(y = 1\).
Đồ thị của hàm số nào trong bốn hàm số sau có đường tiệm cận ngang?
\(y = \frac{x}{{1 + \sqrt x }}\).
\(y = {x^3} - 3x\).
\(y = {\log _2}x\).
\(y = x + \sqrt {{x^2} + 4} \).
Đồ thị của hàm số nào trong các hàm số sau đây có tiệm cận xiên?
\[y = {x^2}\].
\[y = {x^3} - 3x + 4\].
\[y = \frac{{2x + 1}}{{x - 1}}\].
\[y = \frac{{{x^2} - x + 1}}{{x - 1}}\].
Tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + x - 3}}{{x - 1}}\) là:
\[y = 2x - 1\].
\[y = x + 2\].
\[y = 2 - x\].
\[y = x - 1\].
Cho hàm số \(y = \frac{{ - {x^2} + 3x - 1}}{{x - 2}}\). Tọa độ giao điểm của các đường tiệm cận của đồ thị hàm số là:
\(\left( { - 2;\,3} \right)\).
\(\left( {2;\,1} \right)\).
\(\left( {2;\, - 1} \right)\).
\(\left( {3;\,2} \right)\).
Cho hàm số \(y = \frac{{{x^2} + 4x + 16}}{x}\). Tiệm cận xiên của đồ thị hàm số tạo với hai trục tọa độ một tam giác có diện tích bằng
\(8\).
\(16\).
\(4\).
\(12\).
Cho hàm số \(y = \frac{{\left( {m + 1} \right){x^2} + 2x - 1}}{{x - 1}}\) với \(m\) là tham số. Các mệnh đề dưới đây đúng hay sai?
a) Với \(m = - 1\) đồ thị hàm số có tiệm cận ngang \(y = 2\).
b) Với \(m = 0\) đồ thị hàm số có tiệm cận xiên \(y = x - 1\).
c) Với \(m = 2\) thì đường tiệm cận xiên của đồ thị hàm số tạo với hai trục tọa độ một tam giác có diện tích bằng \(\frac{9}{2}\).
d) Với \(m = 1\), tích khoảng cách từ một điểm bất kì trên đồ thị đến các đường tiệm cận bằng \(\frac{{3\sqrt 5 }}{5}\)
Cho hàm số trùng phương \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) có đồ thị như hình vẽ. Xét hàm số \(y = g\left( x \right) = \frac{{{x^2} - 2x}}{{{{\left( {f\left( x \right)} \right)}^2} + 2f\left( x \right) - 3}}\) .
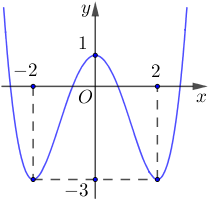
Xét tính đúng sai của các mệnh đề sau.
a) Đồ thị hàm số \(y = g\left( x \right)\)có tổng số tiệm cận đứng và tiệm cận ngang là \(6\).
b) Đồ thị hàm số \(y = g\left( x \right)\) đúng một tiệm cận ngang .
c) Đồ thị hàm số \(y = g\left( x \right)\) có \(3\) tiệm cận đứng.
d) Đồ thị hàm số \(y = g\left( x \right)\) có tổng số tiệm cận đứng và tiệm cận ngang là \(4\).
Cho hàm số \(y = \frac{{2x + m}}{{mx - 3}}\) có đồ thị \(\left( {{C_m}} \right)\), với \(m\) là tham số. Các mệnh đề dưới đây đúng hay sai?
a) Với \(m = - 1\) thì đồ thị hàm số có tiệm cận ngang \(y = 2\).
b) Với \(m = 3\) thì điểm \(A\left( {1;2} \right)\) thuộc tiệm cận đứng của đồ thị hàm số.
c) Với \(m = 1\) thì đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng \(9\).
d) Với \(m = 1\), tích khoảng cách từ một điểm bất kì trên đồ thị đến các đường tiệm cận bằng \(7\).
Cho hàm số \(y = \frac{{{x^2} + \left( {m - 1} \right)x + {m^2} - 2m + 1}}{{1 - x}}\) (1), với \(m\) là tham số. Các mệnh đề dưới đây đúng hay sai?
a) Với \(m = - 1\) thì đồ thị hàm số có tiệm cận xiên đi qua \(M\left( {2; - 3} \right)\).
b) Với \(m = 1\) thì tiệm cận xiên của đồ thị hàm số tạo với hai trục tọa độ một tam giác có diện tích là \(\frac{1}{2}\).
c) Với \(m = 1\) thì tâm đối xứng của đồ thị là điểm \(I\left( {1; - 2} \right)\).
d) Với \(m = 1\)thì tiệm cận xiên, tiệm cận đứng cùng với hai trục tọa độ tạo thành hình thang vuông có diện tích bằng \(3\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ bên dưới
![Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc \(\left[ {0\,;\,10} \right]\) để đồ thị hàm số \(y = \frac{{f\left( x \right)}}{{f\left( x \right) - m + 2}}\) có đúng 4 đường tiệm cận? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/14-1759193871.png)
Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc \(\left[ {0\,;\,10} \right]\) để đồ thị hàm số \(y = \frac{{f\left( x \right)}}{{f\left( x \right) - m + 2}}\) có đúng 4 đường tiệm cận?
Cho hàm số có đồ thị như hình vẽ dưới đây.
![Có bao nhiêu giá trị nguyên của tham số \[m\] để đồ thị hàm số \[g\left( x \right) = \frac{{{x^4} - {x^2} + 2020}}{{{f^2}\left( x \right) - 2\left( {m + 1} \right).f\left( x \right) + 5\left( {2m - 3} \right)}}\] có đúng \[6\] đường tiệm cận. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/15-1759193910.png)
Có bao nhiêu giá trị nguyên của tham số \[m\] để đồ thị hàm số \[g\left( x \right) = \frac{{{x^4} - {x^2} + 2020}}{{{f^2}\left( x \right) - 2\left( {m + 1} \right).f\left( x \right) + 5\left( {2m - 3} \right)}}\] có đúng \[6\] đường tiệm cận.
Cho hàm số \(y = \frac{{2x + 4}}{{\left( {m - 1} \right){x^2} - 2mx - 6}}\). Có bao nhiêu giá trị nguyên của \(m\) trên đoạn \(\left[ { - 2025\,;\,2025} \right]\) để đồ thị hàm số có đúng 3 đường tiệm cận?
Gọi \(S\) là tập hợp các số nguyên \(m\) để đồ thị hàm số \(y = \frac{{\sqrt {1 - x} }}{{{x^2} + 4x + m}}\) có đúng \(3\) đường tiệm cận. Tổng giá trị các phần tử của tập \(S\) bằng bao nhiêu?
Một mảnh đất hình thang vuông có đáy lớn gấp đôi đáy nhỏ, có diện tích là \(S = 24\,\left( {{m^2}} \right)\). Gọi \(x\,\left( m \right)\) là độ dài đáy nhỏ và \(P\left( x \right)\) là chu vi mảnh đất đó. Tìm số tiệm cận của \(P\left( x \right)\).
Chi phí xuất bản \(x\) cuốn tạp chí (bao gồm: lương cán bộ, công nhân viên, giấy in…) được cho bởi \(C\left( x \right) = {x^2} - 2000x + {10^8}\) đồng. Chi phí phát hành cho mỗi cuốn là \(4\) nghìn đồng. \(M\left( x \right) = \frac{{T\left( x \right)}}{x}\) với \(T\left( x \right)\) là tổng chi phí (xuất bản và phát hành) cho \(x\) cuốn tạp chí, được gọi là chi phí trung bình cho một cuốn tạp chí khi xuất bản \(x\) cuốn. Khi số lượng cuốn tạp chí phát hành cực lớn thì chi phí trung bình cho mỗi cuốn tạp chí \(M\left( x \right)\) sẽ tiệm cận với đường nào.
