12 bài tập Một số bài toán thực tế ứng dụng đường tiệm cận của đồ thị hàm số có lời giải

Chi phí (đơn vị: nghìn đồng) để sản xuất x sản phẩm của một công ty được xác định bởi hàm số F(x) = 60000 + 250x. Gọi F(x) là hàm số biểu thị chi phí trung bình (đơn vị: nghìn đồng) để sản xuất x sản phẩm (x ≥ 0), khi đó tiệm cận ngang của đồ thị hàm số bằng

Số dân của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức \(f\left( t \right) = \frac{{26t + 10}}{{t + 5}}\); f(t) được tính bằng nghìn người. Xem f(t) là một hàm số xác định trên nửa khoảng [0; +∞). Đồ thị hàm số y = f(t) có đường tiệm cận ngang y = a. Giá trị của a là bao nhiêu?

Một nhà máy sản xuất linh kiện điện tử thống kê được rằng trung bình một tổ sản xuất với x người thì số sản phẩm sản xuất được trong một thời gian cố định được tính bằng công thức \(P\left( x \right) = \frac{{5000x}}{{4x + 25}}\). Xem y = P(x) là một hàm số xác định trên [0; +∞), khi đó tiệm cận ngang của đồ thị hàm số là:

Số lượng sản phẩm của công ty bán được trong x tháng được tính bởi công thức \(S\left( x \right) = 300\left( {2 + \frac{4}{{x + 2}}} \right)\) với x ≥ 1. Xem y = S(x) là một hàm số xác định trên [1; +∞). Khi đó tiệm cận ngang của đồ thị hàm số là

Dân số P (nghìn người) của một khu nghỉ dưỡng được cho bởi hàm số \(P\left( t \right) = \frac{{400t}}{{2{t^2} + 7}},t \ge 0\), với t là thời gian tính theo tháng. Tìm tiệm cận ngang của đồ thị hàm số y = P(t).

Người ta thống kê được chi phí sửa chữa, vận hành máy móc trong một năm của một xưởng sản xuất được tính bởi công thức \(f\left( x \right) = \frac{{2000x - 1500}}{{35x + 5}}\)(triệu đồng). Biết x là số năm kể từ lúc máy móc vận hành lần đầu tiên, số năm càng nhiều thì chi phí càng cao. Khi số năm x đủ lớn thì chi phí vận hành máy móc trong một năm gần với số nào? (làm tròn đến 1 chữ số thập phân sau dấu phẩy).

Để thiết kế một bể cá không nắp có dạng hình hộp chữ nhật có chiều cao là 80 cm, thể tích là 12800 cm³. Người thợ dùng loại kính để sử dụng làm mặt bên có giá thành 70000 VNĐ/m² và loại kính để làm mặt đáy có giá thành 100000 VNĐ/m². Gọi x là chiều dài của đáy bể cá với (x > 0, x (m)); f(x) là hàm số xác định chi phí để hoàn thành bể cá. Đồ thị hàm số f(x) có bao nhiêu đường tiệm cận?

Số lượng sản phẩm bán được của một cửa hàng quần áo trong t tháng được cho bởi công thức: \(S\left( t \right) = 200\left( {\frac{2}{3} - \frac{8}{{2 + t}}} \right)\) với t ≥ 1. Xem y = S(t) là một hàm số xác định trên nửa khoảng [1; +∞), biết rằng tiệm cận ngang của đồ thị hàm số có dạng \(\frac{a}{b}\,,\,a\,,\,b \in \mathbb{N}*\,,\,\left( {a\,,\,b} \right) = 1\). Tính P = a – 2b.

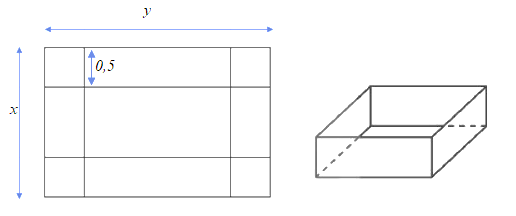
Từ một tấm tôn hình chữ nhật có các kích thước là x (m), y (m) với x > 1, y > 1 và diện tích bằng 4 m², người ta cắt bốn hình vuông bằng nhau ở bốn góc rồi gập thành một cái thùng dạng hình hộp chữ nhật không nắp (như hình vẽ) có chiều cao bằng 0,5 m. Thể tích của thùng là hàm số V(x) trên khoảng (1; +∞). Đồ thị hàm số \(y = \frac{1}{{V\left( x \right)}}\) có bao nhiêu đường tiệm cận đứng?

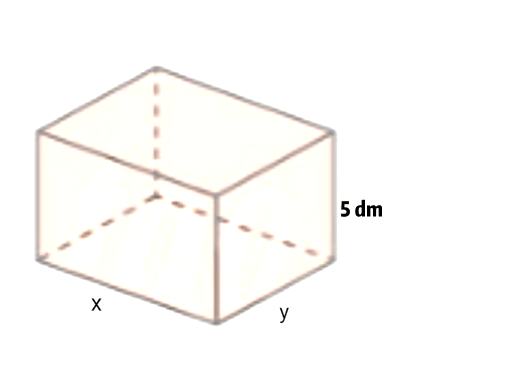
Người ta muốn làm một cái bể dạng hình hộp chữ nhật không nắp (như hình vẽ) có thể tích bằng 1 m³. Chiều cao của bể là 5 dm, các kích thước khác là x (m), y (m) với x > 0 và y > 0. Diện tích toàn phần của bể (không kể nắp) là hàm số S(x) trên khoảng (0; +∞). Đường tiệm cận xiên của đồ thị hàm số S(x) là đường thẳng y = ax + b. Tính giá trị của biểu thức P = a² + b² .