20 câu trắc nghiệm Toán 12 Kết nối tri thức Bài 3. Đường tiệm cận của đồ thị hàm số (Đúng sai - Trả lời ngắn) có đáp án
35 câu hỏi
Cho hàm số y = f(x) có 
và 
. Khẳng định nào sau đây là khẳng định đúng?
Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 1 và x = −1.
Đồ thị hàm số đã cho không có tiệm cận ngang.
Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 1 và y = −1.
Tiệm cận ngang của đồ thị hàm số 
là
y = −2.
y = 1.
x = −1.
x = 2.
Tiệm cận đứng của đồ thị hàm số 
là
x = −3.
x = −1.
x = 1.
x = 3.
Đồ thị của hàm số 
có tiệm cận xiên là
y = 3x – 1.
y = 2 + x.
y = 3 – x.
y = 2x + 1.
Cho hàm số y = f(x) xác định và liên tục trên ℝ\{1} có bảng biến thiên như sau
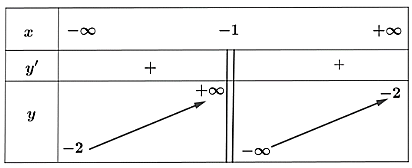
Khẳng định nào sau đây đúng?
Đồ thị hàm số có tiệm cận đứng y = −1 và tiệm cận ngang x = −2.
Đồ thị hàm số có duy nhất một tiệm cận.
Đồ thị hàm số có ba tiệm cận.
Đồ thị hàm số có tiệm cận đứng x = −1 và tiệm cận ngang y = −2.
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?
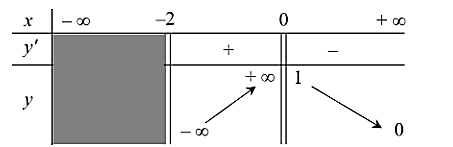
1.
3.
2.
4.
Cho hàm số 
. Tiệm cận xiên của đồ thị hàm số là đường thẳng:
y = 2x – 1.
y = 2x + 1.
y = 2x – 3
y = 2x + 3.
Cho đồ thị hàm số y = f(x) như hình bên
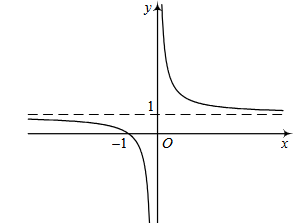
Khẳng định nào sau đây là sai?
Đồ thị hàm số có tiệm cận đứng x = 0.
Đồ thị hàm số có đường tiệm cận đứng và đường tiệm cận ngang.
Đồ thị hàm số có tiệm cận ngang y = 1.
Đồ thị hàm số có tiệm cận đứng x =1 và tiệm cận ngang y = 0.
Cho hàm số 
. Khoảng cách từ gốc tọa độ đến đường tiệm cận đứng bằng
2.
1.
C. 
.
3.
Cho đồ thị của hàm số f(x) như hình bên dưới.
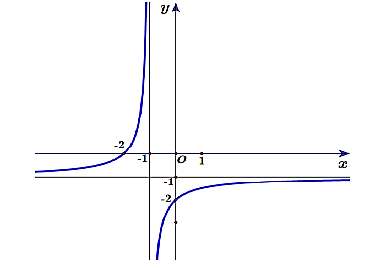
Số đường tiệm cận của đồ thị hàm số f(x) là
2.
1.
0.
3.
a) Hàm số đã cho nghịch biến trên khoảng (−2; 0)
b) Đồ thị hàm số đã cho có tiệm cận ngang
c) Đồ thị hàm số đã cho có hai đường tiệm cận đứng.
d) Hàm số có giá trị lớn nhất trên ℝ.
a) Đồ thị hàm số có tiệm cận đứng x = 1
b) Đồ thị hàm số có tiệm cận ngang y = 0
c) Hàm số đồng biến trên ℝ
d) T = a – 3b – 2c = −3
a) Hàm số có hai tiệm cận
b) Giao điểm của hai tiệm cận là I(−2; −6)
c) Khoảng cách từ O đến tiệm cận xiên bằng 
.
d) Tiệm cận xiên của đồ thị hàm số đi qua điểm M(0; −4)
a) Hàm số đã cho không có cực trị.
b) Đồ thị hàm số có tiệm cận đứng x = −3
c) Đồ thị hàm số có tiệm cận ngang y = −2
d) Các đường tiệm cận của đồ thị hàm số tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 3.
a) Giao điểm của hai đường tiệm cận là I(1; 0)
b) Đồ thị hàm số y = f(x) không cắt trục hoành.
c) Đồ thị hàm số y = f(x) có tiệm cận đứng là đường thẳng có phương trình x = 1.
d) Đồ thị hàm số y = f(x) có tiệm cận xiên là đường thẳng có phương trình y = x.
Số lượng sản phẩm bán được của một cửa hàng quần áo trong t (tháng) được cho bởi công thức 
với t ≥ 1. Xem y = S(t) là một hàm số xác định trên nửa khoảng [1; +∞), biết rằng tiệm cận ngang của đồ thị hàm số có dạng 
(a, b Î ℕ*), (a, b) = 1. Tính P = a – 2b.
Nồng độ oxygen trong hồ theo thời gian t cho bởi công thức 
với y được tính theo mg/l và t được tính theo giờ, t ≥ 0. Đường tiệm cận ngang của đồ thị hàm số y = y(t) khi t → +∞ có dạng y = a. Tính giá trị của a.
Cho hàm số 
có đồ thị như hình vẽ sau:
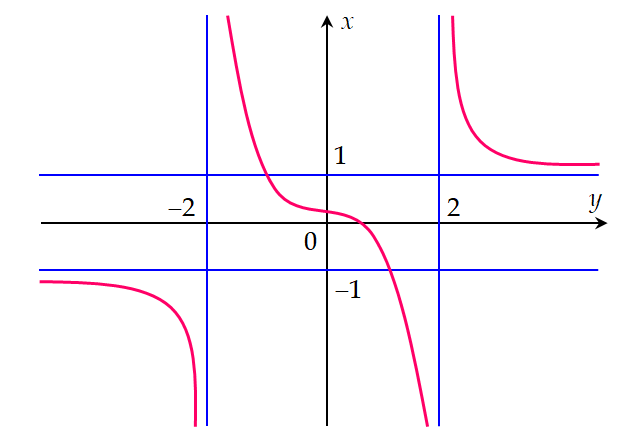
Đồ thị hàm số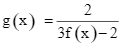
có tất cả bao nhiêu đường tiệm cận?
Cho hàm số 
. Tiệm cận xiên của đồ thị hàm số tạo với hai trục tọa độ một tam giác. Tính diện tích tam giác đó.
Cho hàm số y = f(x) có bảng biến thiên như hình dưới đây
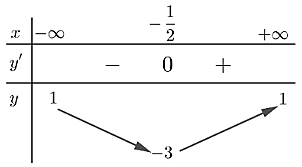
Tìm tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số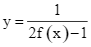 
.
