10000 câu trắc nghiệm tổng hợp môn Toán 2025 mới nhất (có đáp án) - Phần 8

1 cân bằng bao nhiêu gam?

1 dm³ = ? m³

1g = ? kg

Một năm có 365 ngày, 1 ngày có 24 giờ , một giờ có 60 phút. Hỏi một năm có bao nhiêu phút ?

1000 gam bằng bao nhiêu kg?

1 kg bằng bao nhiêu lạng?

0 có phải là một số nguyên không?

số 0 có phải là số nguyên dương không?

Tìm số nguyên y sao cho y ‒ (‒200) là số nguyên dương nhỏ nhất

XIX là số mấy?

Chứng minh bất đẳng thức: \[\frac{1}{x} + \frac{1}{y} \ge \frac{4}{{x + y}}\].

Trắc nghiệm đúng sai.

Biết giới hạn \[\lim \frac{{2n + 1}}{{ - 3n + 2}} = a.\] Khi đó:

a) Giá trị a lớn hơn 0.

b) Ba số \[ - \frac{5}{3};a;\frac{1}{3}\] tạo thành một cấp số cộng với công sai bằng 2.

c) Trên khoảng (‒π; π) phương trình lượng giác sin x = a có 3 nghiệm.

d) Cho cấp số nhân (u_n) với công bội q = 3 thì u₁ = a thì u₃ = ‒6.

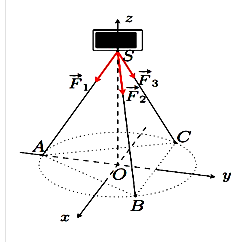
Một chiếc điện thoại iphone được đặt trên một giá đỡ có ba chân với điểm đặt S(0; 0; 20) và các điểm chạm mặt đất của ba chân lần lượt là A(0; ‒6; 0), \[B\left( {3\sqrt 3 ;3;0} \right);C\left( { - 3\sqrt 3 ;3;0} \right)\] (đơn vị cm). Cho biết điện thoại có trọng lượng là 2N và ba lực tác dụng lên giá đỡ được phân bố như hình vẽ là ba lực \[\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \] có độ lớn bằng nhau. Biết tọa độ của lực \[\overrightarrow {{F_1}} = \left( {a,b,c} \right)\]. Khi đó T = 2a + 5b + 6c bằng bao nhiêu?

Cho a + b = 2 và a² + b² = 20. Tính a³ + b³.

Cho tam giác ABC đều có cạnh bằng 8. Biết tập hợp tất cả các điểm N thỏa mãn \[\left| {3\overrightarrow {NA}  - 2\overrightarrow {NB}  + \overrightarrow {NC} } \right| = \left| {\overrightarrow {NB}  - \overrightarrow {NA} } \right|\] là một đường tròn có bán kính R. Tính R.

Cho tam giác ABC. Từ điểm A kẻ tia Am song song với BC. Gọi D là trung điểm của BC. Qua D kẻ đường thẳng bất kì cắt Am tại E, cắt AC tại Q và cắt AB tại P. Chứng minh rằng: \[\frac{{PE}}{{PD}} = \frac{{QE}}{{QD}}.\]

Chứng minh 3 điểm tam giác vuông cùng nằm trên đường tròn?

Cô Phương thống kê lại số giờ chơi thể thao trong 1 tuần của học sinh lớp 10C ở bảng sau:

Chọn đúng hoặc sai.

a) Khoảng biển thiên của mẫu số liệu ghép nhóm trên là 12 giờ.

b) Tứ phân vị thứ nhất của mẫu số liệu gốc thuộc [3; 6).

c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là \[\frac{{681}}{{460}}.\]

d) Phương sai của mẫu số liệu ghép nhóm trên là 7,9236.

Để chuẩn bị cho năm học mới, hai bạn An và Bình cùng đến một cửa hàng để mua bút và vở. Bạn An mua 5 cái bút và 20 quyển vở nên phải thanh toán số tiền là 195 000. Bạn Bình mua 3 cái bút và 20 quyển vở nên phải thanh toán số tiền là 189 000. Biết rằng mỗi cái bút có giá như nhau, mỗi quyển vở có giá như nhau. Tính giá một cái bút và một quyển vở?

Cho hàm số f(x) = (2x + 1)³ có một nguyên hàm là F(x) thỏa mãn \[F\left( {\frac{1}{2}} \right) = 4.\]Hãy tính \[P = F\left( {\frac{3}{2}} \right).\]

Một cửa hàng nhân dịp noel đã đồng loạt giảm giá các sản phẩm. Trong đó có chương trình nếu mua một gói kẹo thứ hai trở đi sẽ được giảm giá 10% so với giá ban đầu là 60000 đồng.

a) Nếu gọi số kẹo đã mua là x, số tiền phải trả là y. Hãy biểu diễn y theo x.

b) Bạn Thư muốn mua 5 gói kẹo thì hết bao nhiêu tiền?

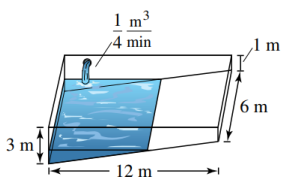
Một hồ bới được chế tạo từ một khối hộp chữ nhật có chiều dài 12m, rộng 6m, sâu 1m ở đầu nông và sâu 3m ở đầu sâu (như hình vẽ). Nước được bơm vào hồ bơi với tốc độ 0,25m khối mỗi phút. Biết rằng trong bể có 1m nước ở đầu sâu. Để lượng nước đạt 75% dung tích bể bơi thì cần bơm trong thời gian bao lâu? (đơn vị tính bằng phút).

Một người đang ở trên tầng thượng của một tòa nhà quan sát con đường chạy thẳng đến chân tòa nhà. Anh ta nhìn thấy một người điều khiển chiếc xe máy đi về phía tòa nhà với phương nhìn tạo với phương nằm ngang một góc bằng 30. Sau 6 phút người quan sát vẫn nhìn thấy người điều khiển chiếc xe máy với phương nhìn tạo với phương nằm ngang một góc bằng 60. Hỏi sau bao nhiêu phút nữa thì xe máy sẽ chạy đến chân tòa nhà? Cho biết vận tốc xe máy không đổi.

Một trường học có hai máy photocopy. Vào một ngày bất kì, máy A có 8% khả năng bị kẹt giấy và máy B có 12 % khả năng bị kẹt giấy. Xác định xác xuất để vào một ngày bất kì, cả hai máy sẽ không bị kẹt giấy.

Tại một cơ sở sản xuất nước tinh khiết, nhân viên phụ trách cho biết, nếu mỗi ngày cơ sở sản xuất x(m³) nước tinh khiết thì phải chi phí các khoản sau: 5 triệu đồng chi phí cố định; 0,15 triệu đồng cho mỗi mét khối sản phẩm; 0,0005x² chi phí bảo dưỡng máy móc. Biết công suất tối đa mỗi ngày của cơ sở này là 200m³. Gọi C(x) là chi phí sản xuất x(m³) sản phẩm mỗi ngày và c(x) là chi phí trung bình mỗi mét khối sản phẩm. Khi đó

a) C(x) = 0,0005x² + 0,15x + 5

b) Chi phí sản xuất 100m³ nước tinh khiết là 20 triệu đồng.

Tính thể tích phần chìm của khối lập phương có cạnh 10cm

Tìm a, b biết a + b = 96 và ƯCLN(a, b) = 12.

Cho tam giác ABC đều cạnh bằng a, M là trung điểm của BC. Tính độ dài vescto AM.

Cho A(‒1; 3; 2), B(4; 0; ‒3), C(5; ‒1; ‒4). Tìm tọa độ điểm đối xứng của A qua đường thẳng BC.

Tính \(\left( {1 - \frac{1}{{15}}} \right)\left( {1 - \frac{1}{{16}}} \right)\left( {1 - \frac{1}{{17}}} \right)...\left( {1 - \frac{1}{{2024}}} \right)\)

Tính

\(\left[ {\left( {1 + \frac{{1999}}{1}} \right)\left( {1 + \frac{{1999}}{2}} \right)...\left( {1 + \frac{{1999}}{{1000}}} \right)} \right]:\left[ {\left( {1 + \frac{{1000}}{1}} \right)\left( {1 + \frac{{1000}}{2}} \right)\left( {1 + \frac{{1000}}{{1999}}} \right)} \right]\)

Tìm x biết 1 + 2 + 3 + … + 100 + 2x = 10000

Tính: \(\frac{1}{{10.11}} + \frac{1}{{11.12}} + ... + \frac{1}{{49.50}}\)

Thực hiện phép tính: \(\left( {\frac{1}{8} + \frac{1}{{8.15}} + ... + \frac{1}{{43.50}}} \right).\frac{{4 - 3 - 5 - 7 - ... - 49}}{{217}}\)

Với x, y, z là các số thực dương thỏa mãn:\(\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = 3\). Tìm giá trị lớn nhất của biểu thức:

\(P = \frac{1}{{\sqrt {2{{\rm{x}}^2} + {y^2} + 3} }} + \frac{1}{{\sqrt {2{y^2} + {z^2} + 3} }} + \frac{1}{{\sqrt {2{{\rm{z}}^2} + {x^2} + 3} }}\)

Tính \(\left( {1 - \frac{1}{{1 + 2}}} \right)\left( {1 - \frac{1}{{1 + 2 + 3}}} \right)...\left( {1 - \frac{1}{{1 + 2 + ... + 2016}}} \right)\)

Tìm x, y biết: (x - 1)²⁰²⁴ + y²⁰²² = 0

Tính nhanh \(\left( {\frac{{13}}{{18}} + \frac{1}{{71}}} \right) - \left( {\frac{{13}}{{18}} - \frac{{70}}{{71}} + \frac{5}{{11}}} \right)\)

Tìm x: (27x + 6) : 3 – 11 = 9

Tìm x biết (2x + 3)² – 2 = 23

Tìm x biết (2x + 4)(x - 3) = 0

Tìm x: (2x - 5)³ = 8

Tìm x: ( 2x – 6 )4⁷=4⁹

Rút gọn \(A = \left( {\frac{{2{\rm{x}}y}}{{{x^2} - {y^2}}} + \frac{{x - y}}{{2{\rm{x}} + 2y}}} \right):\frac{{x + y}}{{2{\rm{x}}}} + \frac{y}{{y - x}}\). ĐKXĐ: x ≠ 0, x ≠ ±y

Tính (500 × 9 − 250 × 18) × (1 + 2 + 3 +…+ 9).

Tìm x biết (5x – 1)(2x – 6) = 0

Tính (−60) + 2².{[(−35) + 5².3] : (−8) – 15}

Phân tích đa thức (a + 2)(a + 3)(a² + a + 6) + 4a² thành nhân tử.

Cho a, b ∈ ℕ và a  + b chia hết cho 7. Chứng minh rằng a + 8b chia hết cho 7.

Cho a, b, c > 0. Chứng minh rằng:

\(\frac{{{a^3}}}{{{a^2} + ab + {b^2}}} + \frac{{{b^3}}}{{{b^2} + bc + {c^2}}} + \frac{{{c^3}}}{{{c^2} + ca + {a^2}}} \ge \frac{{a + b + c}}{3}\)

Chứng minh (a – 1)(a – 2)(a – 3)(a – 4) +1 ≥ 0 với mọi a.

Tìm x biết (x + 1)³ + (x + 2)³ = (2x + 3)³

Giải phương trình \((x + 3)\sqrt {48 - 8{\rm{x}} - {{\rm{x}}^2}}  = x - 24\)

Tìm x sao cho x - 7 chia hết cho x - 3

Rút gọn biểu thức (x + 8)² – 2(x + 8)(x – 2) + (x – 2)²

Phân tích đa thức thành nhân tử: (x² + 1)² – 4x²

Phân tích đa thức thành nhân tử (x² + 3x + 1)(x² + 3x + 2)−6

Tìm cặp số nguyên x, y thỏa mãn: (x – 2019)²⁰²⁰ + (x – 2020)²⁰²⁰ = 2020^{y – 2021}

Tìm a để (x – a)(x – 10) + 1 phân tích được thành tích của các đa thức bậc nhất  với hệ số nguyên.

Chứng minh sin3x – sinx = 2sinx.cosx

Giải phương trình \(\sqrt[3]{{2 - x}} + \sqrt {{\rm{x}} - 1}  = 1\)

 \((\frac{9}{{10}} - \frac{4}{5}):\frac{2}{5} + 1\)

Chứng minh rằng \(\frac{a}{{\sqrt {{a^2} + 8bc} }} + \frac{b}{{\sqrt {{b^2} + 8ac} }} + \frac{c}{{\sqrt {{c^2} + 8ab} }} \ge 1\forall a,b,c > 0\)

Cho hai biểu thức \(N = \frac{{24}}{{\sqrt x  + 6}}\)và \(M = \frac{{\sqrt x }}{{\sqrt x  + 6}} + \frac{1}{{\sqrt x  - 6}} + \frac{{17\sqrt x  + 30}}{{(\sqrt x  + 6)(\sqrt x  - 6)}}\)

a) Rút gọn M

b) Tìm giá trị nguyên x để biểu thức L = M.N có giá trị nguyên lớn nhất.

Tìm x: |x – 3| + |5 – x| +2|x – 4| = 2.

Giải phương trình: \(\sqrt {3{\rm{x}} + 1}  - \sqrt {6 - x}  + 3{{\rm{x}}^2} - 14{\rm{x}} - 8 = 0\)

Giải phương trình: \(\sqrt {7 - x}  + \sqrt {x - 5}  = {x^2} - 12{\rm{x}} + 38\)

Tìm x biết 0,5.[0,5.(x – 0,5) – 0,5] = 0,5

Đổi 0,5dm = …cm

Rút gọn B = (– 5 )⁰ + (– 5)¹ +…+ (– 5)²⁰¹⁷

Tính \(\left( {1 + \frac{{1999}}{1}} \right)\left( {1 + \frac{{1999}}{2}} \right)...\left( {1 + \frac{{1999}}{{1000}}} \right):\left( {1 + \frac{{1000}}{1}} \right)\left( {1 + \frac{{1000}}{2}} \right)...\left( {1 + \frac{{1000}}{{1999}}} \right)\)

Tính \(A = \frac{1}{{1 \times 2}} + \frac{2}{{2 \times 4}} + \frac{3}{{4 \times 7}} + \frac{4}{{7 \times 11}} + \frac{5}{{11 \times 16}} + \frac{6}{{16 \times 22}} + \frac{7}{{22 \times 29}}\)

Tính A = 1 + 2 + 3 + …+ 2022

Chứng minh rằng \(\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{{2022}^2}}} < 1\)

Kết quả phép tính 1 + 3 + 5 + 7 +...+ 19 – 2 – 4 – 6 – 8 − ... – 18 bằng bao nhiêu?

Cho S = 1 + 5 + 5² +…+ 5²⁰¹⁰. Tìm số dư khi chia S cho 2, cho 10, cho 13.

\(\frac{1}{5}\)h = …giây

1g = ? tấn

Một hình thang có chiều cao 12cm, trung bình cộng độ dài hai đáy là 22cm. Thì có diện tích là bao nhiêu?

1 tỷ năm có bao nhiêu ngày

Một vận động viên đi xe đạp trong 3h đầu mỗi giờ đi được 90km, trong 3h sau mỗi giờ đi được 32km. Hỏi người vận động viên đó đi được tất cả bao nhiêu km?

Tìm các chữ số a, b, c trong số thập phân 0,abc (a, b, c khác nhau và khác 0) thỏa mãn:  1 : 0,abc = a + b + c

Chứng minh \(\frac{1}{{1 + 2 + 3}} + \frac{1}{{1 + 2 + 3 + 4}} + ... + \frac{1}{{1 + 2 + ... + 59}} < \frac{2}{3}\)

Tính \(C = \frac{1}{{10}} + \frac{1}{{15}} + \frac{1}{{21}} + ... + \frac{1}{{120}}\)

Tìm x biết: \(\frac{1}{{10}} + \frac{1}{{40}} + \frac{1}{{88}}... + \frac{1}{{\left( {3{\rm{x}} + 2} \right)\left( {3{\rm{x}} + 5} \right)}} = \frac{4}{{25}}\)

Cho A = \(\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{{100}^2}}}\). Chứng minh A < 1.

Tính \(\frac{1}{{2.4}} + \frac{1}{{4.6}} + \frac{1}{{6.8}} + ... + \frac{1}{{98.100}}\)

Cho a, b, c thỏa mãn là số thực không âm thỏa mãn ab + bc + ac = 3.

Chứng minh rằng \(\frac{1}{{{a^2} + 2}} + \frac{1}{{{b^2} + 2}} + \frac{1}{{{c^2} + 2}} \le 1\)

Tìm các số x, y nguyên dương thỏa mãn phương trình \(\frac{1}{x} + \frac{1}{y} = \frac{1}{{617}}\)

10! có bao nhiêu số 0?

Tính \(\frac{{36}}{{ - 84}} + \frac{{100}}{{450}}\)

10000cm² = … m²

\(\left[ {\frac{{109}}{6} - \left( {0,06:\frac{{15}}{2} + \frac{{17}}{5}.0,38} \right)} \right]:\left( {19 - \frac{8}{3}.\frac{{19}}{4}} \right)\)

1100 : 7 =

Tìm x: 12 + 5(x – 1) chia hết cho 6 và 57 < x <75

12000m² = …ha

144 : 6 = bao nhiêu

Đề bài:

Đúng ghi Đ, sai ghi S:

35% của 340kg là 119kg

12,5% của 180m² là 2,25m²

2,5% của 640 học sinh là 160 học sinh

37% của 1,5 tấn là 555kg.

15 giờ trong hệ 24 giờ là mấy giờ trong hệ 12 giờ?