10000 câu trắc nghiệm tổng hợp môn Toán 2025 mới nhất (có đáp án) - Phần 30

Cho A = \(\frac{{12{\rm{n}} + 1}}{{2{\rm{n}} + 3}}\). Tìm giá trị n để

a) A là một phân số.

b) A là một số nguyên.

Cho A = 5⁵⁰ – 5⁴⁸ + 5⁴⁶ – 5⁴⁴ + … + 5⁶ – 5⁴ + 5² – 1

a) Thu gọn A

b) Tìm số tự nhiên n biết: 26.A+1 = 5ⁿ

c) Tìm số dư trong phép chia A cho 100

Cho A = \(\frac{{{\rm{n}}--2}}{{{\rm{n}} + 3}}\). Tìm giá trị n để A là một phân số.

Cho tam giác ABC có \(\widehat A\) = 60°, \(\widehat B\) = 80°, AD là tia phân giác của góc A (D thuộc BC) từ D vẽ đường thẳng song song với AC cắt AB tại M. Từ M vẽ MK song song với AD (K thuộc BC) . Tìm số đo góc ADK

Cho biết y tỉ lệ nghịch với x và khi x = 2 thì y = \(\frac{5}{2}\)

a) Tính giá trị của y khi x = 2; x = -5

b) Tính giá trị của x khi y = 10; y = -3

Cho biểu thức: M = \(\frac{{6{\rm{n}} - 1}}{{3{\rm{n}} + 2}}\). tìm n để biểu thức đó là số nguyên

Chứng tỏ rằng C = 1 + 3 + 3² + 3³ + … + 3¹⁰⁰ chia hết cho 4.

Cho C = 1 + 3 + 3² + 3³ + … + 3³⁰. Chứng tỏ rằng C chia hết cho 4.

Cho dãy số 0; 1; 4; 9; 16;....; 2500

a) Viết tập hợp D gồm các số hạng của dãy số bằng chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó

b) Tập hợp D có bao nhiêu phần tử

Cho đường tròn tâm O đường kính AB. Qua trung điểm I của bán kính OB. Kẻ dây CD vuông góc với AB. Kẻ dây CE song song với AB. Chứng minh rằng:

a) AE = BC = BD

b) E, O, D thẳng hàng

c) Tứ giác ADBE là hình chữ nhật

Cho f(n) = \[\frac{{4{\rm{n}} + \sqrt {4{{\rm{n}}^2} - 1} }}{{\sqrt {2{\rm{n}} + 1} + \sqrt {2{\rm{n}} - 1} }}\]với n nguyên dương.

Tính f(1) + f(2) + f(3) +…+ f(40)

Cho hai vectơ \[{\rm{\vec a}}\] và \[{\rm{\vec b}}\] khác vectơ 0 thỏa mãn \[{\rm{\vec a}}{\rm{.\vec b}} = \frac{1}{2}\left| {{\rm{\vec a}}} \right|{\rm{.}}\left| {{\rm{\vec b}}} \right|\]. Khi đó góc giữa 2 vecto \[{\rm{\vec a}}\] bà \[{\rm{\vec b}}\] là?

Cho hàm số y = mx + 4 (d) với x là biến, m\[ \ne \]0

a) Xác định hàm số biết rằng đồ thị hàm số (d) đi qua điểm A(2; 8)

b) Tìm m để đồ thị hàm số (d) song song với đồ thị hàm số y = 3 - 2x.

c) Tìm giá trị của m để đồ thị hàm số (d) tạo với trục tung và trục hoành một tam giác có diện tích bằng 8 (đơn vị diện tích).

Cho hình chữ nhật ABCD có độ dài cạnh AB = 2a; BC = 4a. Tính độ dài \(\overrightarrow {AB} + \overrightarrow {AC} \)

Cho hình thang vuông ABCD có đáy lớn AB = 8; đáy nhỏ CD = 4; đường cao  AD = 6; I là trung điểm của AD. Tính \(\left( {\overrightarrow {IA} + \overrightarrow {IB} } \right).\overrightarrow {ID} \).

Cho hình vẽ bên dưới, biết AB = 0,6 dm, BC = 4cm. Tính diện tích phần tô đậm.

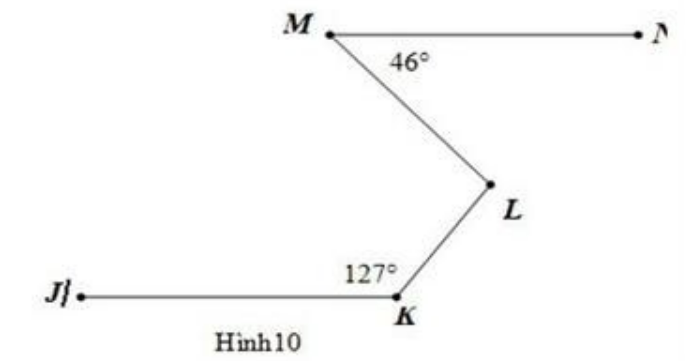
Cho hình vẽ, biết \(\widehat {NML} = 36^\circ ,\widehat {JKL} = 127^\circ \), MN // KJ. Tính số đo góc \(\widehat {MLK}\).

Cho hình vuông có diện tích là 20 cm² và diện tích hình tròn nằm bên trong (hình vẽ). Tính diện tích phần tô đậm.

Cho n lẻ. Chứng minh A = n²⁰⁰⁴ + 1 không phải là số chính phương

Cộng cả tử và mẫu của phân số \(\frac{{12}}{{17}}\) với cùng 1 số tự nhiên x rồi rút gọn được \(\frac{4}{5}\). Tìm x.

Cho phân thức \(D = \frac{{{x^2} - 1}}{{{x^2} + 3x + 2}}\). Rút gọn phân thức giá trị D tại \(x = 2002\)

Tìm m để phương trình 3x² – 5x + m = 0 có 2 nghiệm phân biệt x₁, x₂ sao cho 6x₁ + x₂ = 0

Cho phương trình mx² – 3(m+1)x + m² – 13m – 4 = 0 (với m là tham số). Tìm các giá trị của m để phương trình có một nghiệm là x =-2. Tìm nghiệm còn lại.

Cho \(S = \frac{1}{{{7^2}}} + \frac{2}{{{7^3}}} + \frac{3}{{{7^4}}} + ... + \frac{{69}}{{{7^{70}}}}\). Chứng minh \(S < \frac{1}{{36}}\)

Cho tam giác ABC (AB < AC) vuông tại A. Đường cao AH. Trên cạnh AC lấy điểm E sao cho AH = AE. Qua E kẻ đường thẳng vuông góc với AC cắt BC tại D. Chứng minh tam giác AHD = tam giác AED

Cho tam giác ABC có ba góc nhọn , AB < AC . Qua trung điểm D của cạnh BC kẻ đường thẳng vuông góc với tia phân giác của góc BAC cắt các đường thẳng AB và AC lần lượt tại H và K . Chứng minh rằng : tam giác AHK cân.

Cho tam giác ABC có A(-1; 2), B (0; 3), C(5; -2). Tìm tọa độ chân đường cao hạ từ đỉnh A của tam giác ABC

Cho tam giác ABC có \(\widehat A = 70^\circ \), AD là đường phân giác. Từ D vẽ đường thẳng song song với AB cắt AC ở M. Tính \(\widehat {BAD}\) và \(\widehat {ADM}\)

Cho tam giác ABC có \(AB = 4\sqrt 2 \); AC = 6, \(\widehat {BAC} = 45^\circ \). Gọi D là trung điểm của đoạn thẳng BC. Điểm E thỏa mãn \(AE = k\overrightarrow {AC} \,\,\left( {k \in \mathbb{R}} \right)\). Chứng minh rằng: AD ^ BE khi \(k = \frac{{14}}{{15}}\)

Cho tam giác ABC có \(\widehat B = 45^\circ \), \(AC = 2\sqrt 2 \)cm. Bán kính R của đường tròn ngoại tiếp tam giác ABC bằng:

Cho tam giác ABC có diện tích 64 cm². M là trung điểm của BC, N là trung điểm của AM. Tính diện tích tam giác BNC.

Cho tam giác ABC có E, F lần lượt là trung điểm của AB, AC. Chứng minh: EF // BC (không áp dụng đường trung bình)

Cho tam giác ABC có phương trình đường thẳng BC là 7x + 5y – 8 =0, phương trình các đường cao kẻ từ B, C lần lượt là 9x – 3y – 4 = 0; x + y – 2 = 0. Tìm tọa độ của điểm B và C.

Cho tam giác ABC (AB < AC), đường phân giác AD. Qua trung điểm M của BC, kẻ đường thẳng song song với AD, cắt AC, AB theo thứ tự ở E và K. Gọi O là giao điểm của AM và DK. Chứng minh: AO.OK = DO.OM

Cho tam giác ABC, gọi I là điểm trên BC kéo dài sao cho IB = 3IC. Gọi J và K lần lượt là hai điểm trên cạnh AC, AB sao cho JA = 2JC, KB = 3KA. Biểu diễn \(\overrightarrow {BC} \) theo \(\overrightarrow {AI} ,\,\,\overrightarrow {JK} \)

Cho tam giác ABC. Gọi M là trung điểm AB, D là trung điểm BC, N là điểm thuộc AC sao cho \(\overrightarrow {CN} = 2\overrightarrow {NA} \). K là trung điểm MN. Chứng minh \(KD = \frac{1}{4}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \).

Cho tam giác ABC. Tìm điểm M sao cho: \(2\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \)

Cho tam giác ABC. Điểm I trên cạnh AC sao cho \(CI = \frac{1}{4}CA\). J là điểm mà \(\overrightarrow {BJ} = \frac{1}{2}\overrightarrow {AC} - \frac{3}{2}\overrightarrow {AB} \). Chứng minh \(\overrightarrow {BI} = \frac{3}{4}\overrightarrow {AC} - \overrightarrow {AB} \)

Cho tập hợp A có 7 phần tử của tập hợp A có bao nhiêu tập hợp con mà số phần tử của nó không ít hơn 3 phần tư

Cho tập hợp A = {x Î\(\mathbb{Z}\)| \(\left| {x - 1} \right| < 3\)}. Có bao nhiêu tập hợp con của tập hợp A có đúng 4 phần tử.

Cho tổng S = 3¹ + 3² + 3³ + ...+ 3²⁰. Chứng tỏ S chia hết cho 12

Cho x, y là các số hữu tỉ và thỏa mãn đẳng thức x³ + y³ = 2xy. Chứng minh rằng: \(\sqrt {1 - xy} \) là một số hữu tỉ.

Cho x,y là 2 số nguyên thỏa mãn x + 2019x² = 2020y² + y. Chứng minh rằng: x – y là số chính phương.

Cho X = {4; 5}. Số tập con có một phần tử của X là:

Chú Năm có một mảnh đất dạng hình chữ nhật với chiều dài 8 m, chiều rộng 4,6 m. Chú đã dùng \(\frac{1}{4}\) mảnh đất đó để trồng hoa và dùng phần còn lại để trồng rau. Tính diện tích chú Năm dùng để trồng rau.

Chữ số 4 trong số thập phân 53,412 có giá trị là bao nhiêu?

Nửa hình tròn có đường kính là 6 cm. Tính chu vi nửa hình tròn và cả hình tròn

Tính chu vi hình vuông biết cạnh là 1 cm

Chu vi của 1 hình vuông tăng 20%. Hỏi diện tích của hình vuông đó tăng bao nhiêu phần trăm?

Chứng minh rằng: \(\frac{{2n + 3}}{{3n + 4}}\) là phân số tối giản với số tự nhiên n.

Chứng minh rằng các số 3ⁿ + 4 không là số chính phương

Một vật hình trụ tròn đặc làm bằng nhôm có chiều cao 20cm bán kính đáy là 2cm. Cho khối lượng riêng của nhôm là 2,7g/cm³. Khối lượng của khối trụ là?

Một vòi nước chảy vào bể trong 2 giờ thì đầy bể. Hỏi nếu có 2 vòi nước như vậy cùng chảy thì sau bao lâu sẽ đầy bể?

Mua 8 quyển vở hết 52 000 đồng. Hỏi mua 5 quyển vở hết bao nhiêu tiền?

Năm tay tổng số tuổi của hai ông cháu là 76 tuổi. Biết ông hơn cháu 66 tuổi. Tính số tuổi của ông và cháu.

Tích của hai số là 135. Nếu tăng thừa số thứ hai 4 đơn vị thì tích tăng thêm 180 đơn vị. Tìm thừa số thứ nhất.

Tìm x biết 5^x+1 – 5^x = 2.2^x + 8.2^x

Cho x + y + z = 1.

Chứng minh rằng giá trị biểu thức \[P = \frac{{{{\left( {x + y} \right)}^2}}}{{xy + z}}.\frac{{{{\left( {y + z} \right)}^2}}}{{yz + x}}.\frac{{{{\left( {z + x} \right)}^2}}}{{z{\rm{x}} + y}}\] không phụ thuộc vào giá trị của biến số

Chuyển về tỉ số phần trăm và số thập phân \(\frac{{28}}{{35}}\)

Quãng đường từ trung tâm Hà Nội đến Sơn Tây là 41km. Trên bản đồ tỉ lệ 1: 1 000 000, quãng đường đó dài bao nhiêu milimet?

Quy đồng mẫu số \(\frac{3}{4}\)và \(\frac{7}{8}\)

Rút gọn A = 1 + 2 + 3 +…+ 100

Rút gọn phân số: \(\frac{{125}}{{175}}\)

Tính tổng S = 3 + 2² – 2³ + 2⁴ – … – 2⁹⁹ + 2¹⁰⁰

Người ta sắp xếp 27 hình lập phương nhỏ thành hình lập phương lớn, sau đó sơn tất cả các mặt của hình lập phương lớn.

a) Có bao nhiêu hình lập phương nhỏ được sơn?

b) Có bao nhiêu hình lập phương nhỏ được sơn 3 mặt, 2 mặt, 1 mặt?

Sắp xếp các phân số theo thứ tự tăng dần \(\frac{{ - 1}}{2};\frac{5}{{12}};\frac{7}{{18}};\frac{{ - 5}}{9};\frac{{ - 1}}{3};\frac{1}{3}\)

số 100! có bao nhiêu chữ số 0 tận cùng?

Số bé nhất có 7 chữ số mà tổng các chữ số bằng 31 là:

Số 2025²⁰²⁵ có bao nhiêu chữ số?

Tìm số dư khi A = 7 + 7² + 7³ + ... + 7⁹⁹ cho 8. Hãy giải thích vì sao ra số dư đó.

Số kẹo của An bằng \(\frac{2}{3}\) số kẹo của Bình. An cho Bình 6 cái kẹo thì số kẹo của An bằng \(\frac{3}{7}\) số kẹo của Bình. Hỏi lúc đầu mỗi bạn có bao nhiêu cái?

Số lớn nhất có 7 chữ số mà tổng các chữ số bằng 31 là:

Số nguyên tố lớn nhất có hai chữ số?

So sánh: \(\frac{{{{100}^{2015}} + 1}}{{{{100}^{2005}} + 1}}\) và \(\frac{{{{100}^{2016}} + 1}}{{{{100}^{2006}} + 1}}\)

so sánh 3⁴⁰⁰ và 4³⁰⁰

Số thập phân nhỏ nhất có 3 chữ số lớn hơn 8

Cho tam giác ABC có số đo cạnh BC bằng 32 cm, biết rằng nếu kéo dài đoạn BC thêm 4 cm thì diện tích tam giác sẽ tăng 54 cm². Hỏi diện tích tam giác ABC bằng bao nhiêu?

Tam giác ABC có góc A vuông, AB = 40 m, AC = 30 m; BC = 50 m. Trên AC lấy F, trên AB lấy E sao cho EFCB là hình thang có chiều cao là 12 m. Tính diện tích tam giác AFE và FEBC

tan(x² + 2x + 3) = tan 2

Tìm a, b là các số nguyên dương sao cho a + b² chia hết cho a²b – 1.

Trong mặt phẳng Oxy, phép vị tự tâm I tỉ số k =-2 biến điểm A(3; 2) thành điểm B(9, 8). Tìm tọa độ tâm vị tự I.

Tiền công quét sơn 6m tường rào là 180 000 đồng. Hỏi tiền công quét sơn 25 m tường rào như thế là bao nhiêu đồng?

Tìm các số a, b, c biết \(\frac{a}{2} = \frac{b}{3} = \frac{c}{5}\) và a – 3b + 2c = 30.

Tìm a, b, c biết \(\frac{{a - 1}}{2} = \frac{{b - 2}}{3} = \frac{{c - 3}}{4}\) và a – 2b + 3c = 14.

Tìm các số có dạng 21a5b chia hết cho 4 và 7.

Tìm các số x, y, z nguyên dương thỏa mãn x³ + 3x² + 5 = 5^y và x + 3 = 5^z

Tìm cặp số tự nhiên (m; n) thỏa mãn hệ thức: m² + n² = m + n + 8

Tìm các số nguyên t sao cho \(\frac{{5t + 2}}{{17}}\) là một số nguyên

Tìm các số nguyên x, y sao cho (y + 2).x² + 1 = y²

Tìm số a và số nguyên x sao cho (12 + 3x)² = 1a96

Tìm điều kiện xác định của phân thức \(\frac{{{x^2} + 3}}{{{x^2} - 6x + 9}}\)

Tìm giá trị nhỏ nhất của biểu thức M = (2x – 4)¹⁰ + 5(y + 3)⁴ + 10

Tìm giá trị nhỏ nhấtcủa biểu thức: B = xy(x – 2)(y + 6) + 12x² – 24x + 3y³ + 18y + 2045

Tìm giá trị nhỏ nhất của biểu thức \(\frac{{x + 3}}{{\sqrt x }}\)

Tìm hai chữ số tận cùng của \({99^{{{99}^{99}}}}\).

Tìm hai số biết tổng và hiệu của chúng lần lượt là 123 và 45

Xác định số hữu tỉ a và b sao cho: \({x^2} - ax - 5{a^2} - \frac{1}{4}\) chia hết cho x + 2a

Tìm giá trị nguyên của k để phương trình sau có nghiệm là số hữu tỉ kx² – (1 – 2k)x + k – 2 = 0

Tìm các số tự nhiên n để phân số \(\frac{{3n + 2}}{{7n + 1}}\) là phân số tối giản