10000 câu trắc nghiệm tổng hợp môn Toán 2025 mới nhất (có đáp án) - Phần 26

Tìm một số là bội của 50 biết hai lần số đó là một số nhỏ hơn 101.

Viết số:

4 triệu, 2 trăm nghìn, năm chục

2 chục nghìn, 5 nghìn, 6 trăm, 7 đơn vị

3 trăm linh tám triệu, không trăm mười nghìn.

Dấu hiệu chia hết cho 9 là gì?

Từ 1 đến 100 có bao nhiêu số chính phương, đó là những số nào?

Viết các số la mã từ 1 đến 20

Viết các số nguyên tố nhỏ hơn 100.

Cánh đồng lúa của xã A rộng 22 km², cánh đồng lúa của xã A nhỏ hơn 3 lần cánh đồng lúa của xã B là 14 km². Trung bình cứ 1 hm² người ta thu hoạch được \[8\frac{1}{2}\] tấn lúa. Hỏi cả hai xã thu hoạch được bao nhiêu tấn lúa trên cánh đồng đó?

Tìm m để hai đường thẳng (d₁): y = mx + 5 ‒ m và (d₂): y = 3x + m ‒ 1 cắt nhau tại một điểm nằm trên trục tung.

Cho 1 hình chữ nhật có diện tích là 486 cm². Nếu giảm chiều dài xuống 3 lần, giảm chiều rộng xuống 2 lần thì được một hình vuông. Tính chu vi hình chữ nhật.

Cho 8 điểm trong đó không có 3 điểm nào thẳng hàng. Cứ qua 2 điểm ta vẽ một đường thẳng. Hỏi có tất cả bao nhiêu đường thẳng?

Cho A, B là hai biến cố độc lập. Biết \[P\left( A \right) = \frac{1}{4}\], \[P\left( {A \cap B} \right) = \frac{1}{9}\]. Tính P(B).

Cho các số: 7, 11, 13, 23. Hãy viết tất cả các phân số có tử số và mẫu số là các số đã cho mà tử số khác mẫu số.

Cho các số: 27501, 106712, 7110385, 2915404267 (viết trong hệ thập phân)

a) Đọc mỗi số đã cho.

b) Chữ số 7 trong mỗi số đã cho có giá trị là bao nhiêu?

Cho đa thức P(x) = ax² + bx + c biết 7a ‒ b + 4c = 0. Chứng minh P(2) . P(‒1) không là số dương.

Cho dãy số: 2, 5, 8, 11,...Số thứ 150 của dãy số là bao nhiêu?

Cho dãy số: 3, 18, 48, 93, 153.

a) Tìm số thứ 100 của dãy số.

b) 11703 là số hạng thứ mấy ?

Cho f(x) = ax² + bx + c nhận giá trị nguyên với mọi giá trị nguyên của x. Chứng minh rằng 2a, a + b và c là các số nguyên.

Cho hàm số y = (a ‒ 1)x + a. Tìm a để đồ thị hàm số:

a) Đi qua điểm A(1; 2)

b) Cắt trục tung tại điểm có tung độ bằng ‒2

c) Cắt trục hoành tại điểm có trục hoành bằng 3

d) Song song với đường thẳng y = 2x + 3

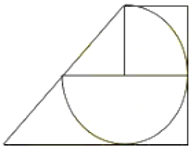
Cho hình bên. Tính diện tích hình thang, biết bán kính hình tròn là 5cm và đáy lớn gấp 3 lần đáy bé.

Cho hình bình hành ABCD. Ở miền trong hình bình hành ABCD vẽ hình bình hành A’B’C’D’. Gọi M, N, P, Q lần lượt là trung điểm của AA’, BB’, CC’, DD’. Chứng minh rằng tứ giác MNPQ là hình bình hành.

Cho hình bình hành ABCD tâm O. Gọi M, N lần lượt là trung điểm BO, AO. Lấy điểm F trên cạnh AB sao cho tia FM cắt cạnh BC tại E và tia FN cắt cạnh AD tại K. Chứng minh rằng: \[\frac{{BA}}{{BF}} + \frac{{BC}}{{BE}} = 4\].

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi H, I, K lần lượt là trung điểm của SA, SB, SC, M là giao điểm của AI và KD, N là giao điểm của DH và CI.

a) Chứng minh rằng SM // (ABCD).

b) Chứng minh rằng (SMN) // (ABCD).

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a tâm O, SA vuông góc với (ABCD) và SA = 3a. Tính khoảng cách từ C đến (SBD).

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = 10cm, đường cao SO bằng 12cm.

a) Vẽ hình và tính thể tích của hình chóp đều.

b) Tính diện tích xung quanh của hình chóp.

Cho hình chữ nhật ABCD. Trên cạnh DC lấy điểm M sao cho \[DM = \frac{1}{3}DC.\] Biết AD = 15cm, AB = 24cm. Tính:

a) Chu vi hình chữ nhật ABCD.

b) Diện tích tam giác AMC.

c) Tính tỉ số phần trăm diện tích của hình tam giác ADM và hình thang ABCM.

Cho hình thang ABCD (AB // CD) có AC ⊥ BD. Biết AC = 6cm, BD = 18cm. Tính chiều cao hình thang.

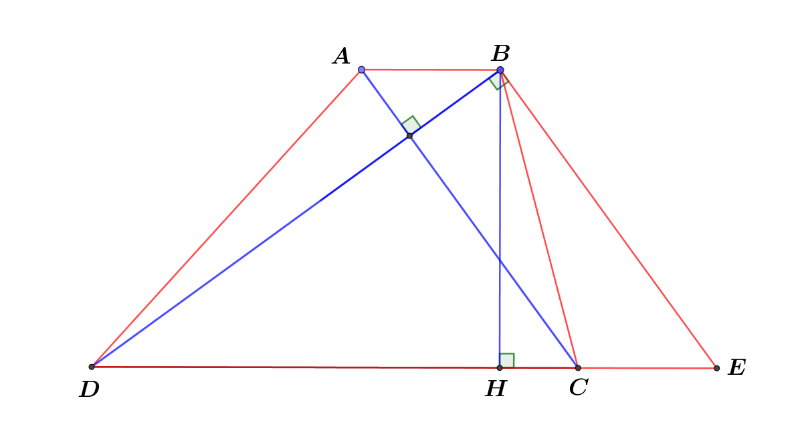
Cho hình thang ABCD (AB // CD) có đáy nhỏ AB = BC. Chứng mình CA là tia phân giác của \[\widehat {BCD}.\]

Cho hình vuông ABCD biết diện tích hình vuông có cạnh gấp 2 lần cạnh hình vuông ABCD là 144m². Hỏi hình vuông có cạnh gấp 3 lần cạnh hình vuông ABCD có diện tích là bao nhiêu m²?

Cho hình vuông ABCD cạnh a. Tính các tích vô hướng sau:

a) \[\overrightarrow {AB}  \cdot \overrightarrow {AD} ;\overrightarrow {AB} \cdot \overrightarrow {BD} \]

b) \[\left( {\overrightarrow {AB} + \overrightarrow {BD} } \right) \cdot \left( {\overrightarrow {BD} + \overrightarrow {BC} } \right)\]

Cho phân số \[\frac{9}{{34}}.\] Hãy tìm số tự nhiên m sao cho khi đem cả tử số và mẫu số của phân số đã có trừ đi số m ta được phân số mới. Rút gọn phân số mới ta được phân số \[\frac{1}{6}.\]

Cho tam giác ABC có A(‒1; 0), B(4; 0), C(0; m), m ≠ 0. Gọi G là trọng tâm của tam giác ABC. Xác định m để tam giác GAB vuông tại G.

Cho tam giác ABC biết \[\widehat {A\,}:\widehat {B\,}:\widehat {C\,} = 3:5:7.\]So sánh các cạnh của tam giác ABC.

Cho tam giác ABC đường cao AH, BK (H thuộc BC, K thuộc AC). Kẻ HM vuông góc với AC (M thuộc AC).

a) Chứng minh tam giác CHM đồng dạng với tam giác CAH.

b) Chứng minh BC² = 2CK.CA.

Cho tam giác ABC cân tại A và M là trung điểm của BC.

a) Chứng minh rằng ∆AMB = ∆AMC.

b) Chứng minh AM là tia phân giác của góc BAC.

c) Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh rằng AB // CD.

Cho tam giác ABC có 3 góc nhọn và 3 đường cao AD, BE, CF.

a) Chứng minh tam giác ABE đồng dạng với tam giác ACF.

b) Chứng minh: CD.CB = CE.CA.

Cho tam giác ABC có \(\widehat {A\,} = 60^\circ .\) Vẽ ra ngoài của tam giác hai tam giác đều AMB và ANC.

a) Chứng minh rằng 3 điểm A, M, N thẳng hàng.

b) Chứng minh BN = CM.

Cho tam giác ABC có trung tuyến AM. Trên cạnh AC lấy hai điểm E và F sao cho AE = EF = FC, BE cắt AM tại N. Chứng minh \[\overrightarrow {NA} \] và \[\overrightarrow {NM} \] là hai vectơ đối nhau.

Cho tam giác ABC. Gọi M là trung điểm của BC, gọi N là trung điểm của AB. Biết diện tích tam giác AMN bằng 6 cm². Tính diện tích tam giác ABC.

Cho tam giác ABC nhọn, lấy điểm M là trung điểm của cạnh AB, lấy điểm N là trung điểm của cạnh AC. Trên tia đối của tia NM lấy điểm Qsao cho NM = NQ. Chứng minh rằng:

a) Hai tam giác AMN và CQN bằng nhau.

b) MB song song với QC.

c) \[MN = \frac{1}{2}BC.\]

Cho tam giác ABC nhọn có AB < AC. Các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC. Từ B kẻ đường thẳng vuông góc với AB và từ C kẻ đường thẳng vuông góc với AC, hai đường thẳng này cắt nhau tại K.

a) Chứng minh BHCK là hình bình hành.

b) Chứng minh H, M, K thẳng hàng.

c) Chứng minh tam giác MEF là tam giác cân.

Cho tam giác ABC vuông tại A (AB < AC), gọi M là trung điểm của BC. Qua M kẻ các đường thẳng song song với AB, AC cắt AC và AB lần lượt tại N và P.

a) Chứng minh ANMP là hình chữ nhật.

b) Gọi Q là điểm đối xứng với M qua N. Chứng minh tam giác AMCQ là hình thoi.

Cho tam giác ABC vuông tại A (AB < AC), đường cao AH.

a) Chứng minh tam giác ABH đồng dạng với tam giác ABC.

b) Chứng minh AH² = HB.HC.

c) Trên tia HC, lấy điểm D sao cho HD = HA. Từ D vẽ đường thẳng song song AH cắt AC tại E. Chứng minh AE = AB.

Cho tam giác ABC vuông tại A đường cao AH (H ∈ BC). Biết AB = 3cm, AC = 4cm.

a) Chứng minh ∆HBA ᔕ ∆ABC.

b) Tính độ dài đường cao AH.

c) Đường phân giác của \(\widehat {ABC}\) cắt AH, AC lần lượt tại M, N. Chứng minh MA.NA = MH.NC.

Cho tam giác ABC vuông tại A và AH vuông góc với BC (H thuộc BC).

a) Chứng minh \[\widehat {BAH} = \widehat {BCA}.\]

b) Tia phân giác của \[\widehat {BAH}\] cắt CH tại K. Chứng minh \[\widehat {AKH} = \widehat {CAK}.\]

Cho tam giác ABC, D là trung điểm của BC. Trên AD lấy điểm E sao cho AE gấp đôi ED. Nối B với E và kéo dài cắt AC tại G. Chứng minh G là trung điểm của AC.

Cho tam giác DEF cân tại D. Trên cạnh DE và DF lần lượt lấy 2 điểm H và K sao cho DH = DK. Gọi giao điểm của EK và FH là O. Chứng minh rằng:

a) EK = FH.

b) ∆HOE = ∆KOF.

c) DO ⊥ EF.

Cho tam giác MNP vuông tại M đường cao MH, phân giác MD. Biết MN = 18 cm, MP = 24 cm. Tính độ dài NH, MH, HD.

Cho tam giác ABC là tam giác nhọn cân tại A. Kẻ hai đường cao BH và CK.

a) Chứng minh rằng đường tròn tâm O đường kính BC đi qua K và H.

b) Chứng minh rằng cung BH bằng cung CK.

c) Tính số đo cung KH nếu \[\widehat {BAC} = 40^\circ .\]

Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H. Gọi P là giao điểm của BE và DF. Chứng minh rằng:

a) H là giao điểm của 3 đường phân giác của tam giác DEF.

b) \[\frac{{HP}}{{HE}} = \frac{{BP}}{{BE}}.\]

Cho tam giác OAB vuông cân tại O, cạnh OA = 4 cm. Tính \[\left| {2\overrightarrow {OA} - \overrightarrow {OB} } \right|.\]

Cho các tập hợp A = {0; 3; 4; 6}. Số tập hợp con gồm 2 phần tử của A là:

A. 12.

B. 8.

C. 10.

D. 6.

Chọn phát biểu sai:

A. Một điểm có thể thuộc đồng thời nhiều đường thẳng.

B. Với một đường thẳng a cho trước, có những điểm thuộc a và có những điểm không thuộc a.

C. Trên đường thẳng chỉ có một điểm.

D. Một điểm có thể thuộc đồng thời hai đường thẳng.

Chữ B có trục đối xứng không?

Kể tên một vài kiểu chữ in hoa có 1 trục đối xứng, 2 trục đối xứng

Chữ H có tâm đối xứng không?

Chữ N có tâm đối xứng không?

Muốn tính chu vi mặt đáy của hình hộp chữ nhật ta làm như thế nào?

Tính nửa chu vi hình tròn biết đường kính hình tròn là 6 cm.

Chữ Z có trục đối xứng không?

Có bao nhiêu cách chứng minh 3 đường thẳng đồng quy?

Trình bày các cách chứng minh tam giác cân.

Trình bày cách chứng minh tam giác đều.

Trình bày cách chứng minh tia phân giác.

Trình bày cách chứng minh trung điểm.

Để chuyển từ phân số sang số thập phân ta làm thế nào?

cm³ là gì?

Có 3 xe chở gạo, xe thứ nhất chở được 3,8 tấn; xe thứ hai chở được 4,3 tấn; xe thứ 3 chở được 4,5 tấn. Hỏi trung bình mỗi xe chở được bao nhiêu tạ gạo, bao nhiêu tấn gạo?

Một năm có bao nhiêu ngày?

Có bao nhiêu số lẻ có 2 chữ số?

Có bao nhiêu số tự nhiên có 2 số? Tính tổng của chúng.

Có bao nhiêu số tự nhiên từ 1 đến 20 không nguyên tố cùng nhau với số 15?

A. 11 số

B. 10 số

C. 9 số

D. 8 số

Có bao nhiêu tháng 28 ngày?

Cô Mai có 60 m lưới muốn rào một mảnh vườn hình chữ nhật để trồng rau. Biết rằng một cạnh là tường (nên không cần rào). Cô Mai chỉ cần rào ba cạnh còn lại của hình chữ nhật để làm vườn. Để diện tích mảnh vườn không ít hơn 400 m² thì chiều rộng của vườn cần có giá trị nhỏ nhất là bao nhiêu?

Muốn tính chiều rộng hình chữ nhật ta làm thế nào?

Muốn tính chu vi mặt đáy hình hộp chữ nhật khi biết chiều cao và diện tích xung quanh ta làm thế nào?

Công thức lũy thừa một tích, lũy thừa một thương.

Công thức tính số số hạng và tổng một dãy.

Cứ 5 ô tô tải như nhau chở được 15 tấn hàng. Hai đoàn xe vận tải có sức chở như thế. Đoàn thứ 1 có 12 xe, đoàn thứ 2 có 18 xe. Hỏi cả hai đoàn chở được bao nhiêu tấn hàng?

Cửa hàng ban đầu bán một đôi giày giá 400 000 đồng. Lần thứ nhất hạ giá 12% giá ban đầu. Cuối năm lại tiếp tục hạ tiếp 10% giá trước đó. Hỏi sau hai lần hạ giá đôi giày đó giá bao nhiêu tiền?

Cửa hàng có số gạo tẻ nhiều hơn số gạo nếp là 1 tạ 50 kg. Sau khi bán đi 25 kg gạo mỗi loại thì còn lại lượng gạo nếp bằng \[\frac{2}{5}\] lượng gạo tẻ. Hỏi lúc đầu cửa hàng có bao nhiêu kg gạo mỗi loại?

Đa thức là gì?

Dấu hiệu chia hết cho 2 là gì?

Dấu hiệu chia hết cho 2, 3, 5, 9 là gì?

Dấu hiệu chia hết cho 3?

Dấu hiệu chia hết cho 3 và 5?

Dấu hiệu chia hết cho 4?

Dấu hiệu chia hết cho 5?

Dấu hiệu chia hết cho 6?

Dấu hiệu chia hết cho 8?

Dấu hiệu chia hết cho 9?

Dãy số lẻ từ 1 đến 118 là: 1, 3, 5,..., 115, 117. Dãy số hạng trên có bao nhiêu số hạng?

Viết dãy số π đầy đủ.

Tổng các chữ số từ 1 đến 1000 là bao nhiêu?

Tìm m để phương trình có 2 nghiệm phân biệt: \[\sqrt {{x^2} + mx + 2} = 2x + 1.\]

Điểm thuộc đồ thị hàm số y = 2x ‒ 5 là:

A. (4; 3)

B. (3; ‒1)

C. (‒4; ‒3)

D. (2; 1)

Tính diện tích mặt đáy của hình hộp chữ nhật có chiều dài a, chiều rộng b, chiều cao h (cùng đơn vị đo).

Công thức tính diện tích đáy của hình lăng trụ đứng.

Tính diện tích nửa hình tròn có đường kính là 6 cm.

Diện tích tờ giấy kiểm tra của em khoảng:

A. 605dam².

B. 605hm².

C. 605cm².

D. 605 mm².