10000 câu trắc nghiệm tổng hợp môn Toán 2025 mới nhất (có đáp án) - Phần 20

Cho hệ phương trình tham số m: \(\left\{ \begin{array}{l}x + my = 3\\mx + y = 2m + 1\end{array} \right.\)

Biết hệ có nghiệm duy nhất (x;y). Tìm giá trị nhỏ nhất P = x² + 3y²

Giải hệ phương trình: \(\left\{ \begin{array}{l}x + y + \frac{1}{x} + \frac{1}{y} = \frac{9}{2}\\\frac{1}{4} + \frac{3}{2}\left( {x + \frac{1}{y}} \right) = xy + \frac{1}{{xy}}\end{array} \right.\)

Tính số đo của góc x và góc y trong hình 9, biết 2x = 3y

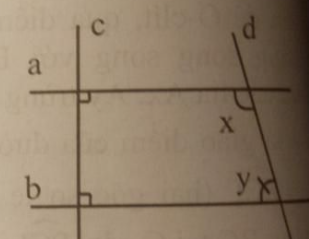
Giải hệ phương trình \(\left\{ \begin{array}{l}x + y + xy + 1 = 0\\{x^2} + {y^2} - x - y = 22\end{array} \right.\)

Cho x + y + z = 1. Chứng minh giá trị biểu thức sau không phụ thuộc vào giá trị của biến, \(P = \frac{{{{\left( {x + y} \right)}^2}}}{{xy + z}}.\frac{{{{\left( {y + z} \right)}^2}}}{{yz + x}}.\frac{{{{\left( {x + z} \right)}^2}}}{{zx + y}}\)

Giải hệ phương trình: \(\left\{ \begin{array}{l}x + y + z = 1\\{x^4} + {y^4} + {z^4} = xyz\end{array} \right.\)

Tìm số hữu tỉ x, y biết: x + y = 3(x - y) = \(\frac{{2x}}{y}\)

Tìm giá trị nhỏ nhất của biểu thức A = x(x + 1)(x + 2)(x + 3)

Tìm các số nguyên x sao cho x(x – 1)(x – 7)(x – 8) là số chính phương

Tìm x biết: \(\frac{x}{{4,45}} - 2 = 1,7\)

Tìm x, y, z biết: \(\frac{x}{4} = \frac{{ - 9}}{y} = \frac{z}{8} = \frac{{ - 24}}{{32}}\)

Thu gọn S = x⁰ + x¹ + x² + x³ + … + xⁿ

Giải phương trình: x² + 7x – 18 = 0

Giải phương trình nghiệm nguyên x² + x + 1 = 2xy + y

Khai triển hằng đẳng thức x² – y²

Cho phương trình x² − 2(m + 1)x + m² = 0. Tìm m để phương trình có đúng một nghiệm.

Phân tích đa thức thành nhân tử x² - y² - 4x - 2y + 3

Giải hệ phương trình: \(\left\{ \begin{array}{l}{x^2} - {y^2} = 4x - 2y - 3\\{x^2} + {y^2} = 5\end{array} \right.\)

Tìm x, y là các số nguyên tố sao cho x² + 3xy + y² là số chính phương

Chứng minh rằng nếu x, y là hai số nguyên dương thoả mãn x² + 4xy - 8y²- 4y + 1= 0 thì 2y - x là số chính phương

Tìm nghiệm nguyên của phương trình: x² + xy + y² = x – y

Giải hệ phương trình \(\left\{ \begin{array}{l}{x^2} + {y^2} + 2\left( {xy + 3x - y} \right) = 0\\{x^2} + {y^2} + 4x - 2y = 0\end{array} \right.\)

Giải hệ phương trình \(\left\{ \begin{array}{l}{x^2} + {y^2} + 4x + 2y = 0\\{x^2} + 7{y^2} - 4xy + 6y = 13\end{array} \right.\)

Trên tập hợp Z các số nguyên. Chứng minh rằng x² + y² chia hết cho 5 khi và chỉ khi x và y đồng thời chia hết cho 5

Cho x² + y² – xy = 3; và x + y = \[\frac{2}{{{x^2} - xy + {y^2}}}\]. Chứng minh rằng x³ + y³ = 2

Tìm nghiệm nguyên dương của phương trình: x² + y² + z² + xyz = 20

Tìm các số nguyên x, y, z thỏa mãn: x² + y² + z² + 14 = 2x + 4y + 6z

Giải hệ phương trình \(\left\{ \begin{array}{l}{x^2} + x + {y^2} + y = 18\\xy\left( {x + 1} \right)\left( {y + 1} \right) = 72\end{array} \right.\)

Cho phương trình x² + (m – 4)x – m + 3 = 0, m là tham số

Tìm m để phương trình nhận \(x = 5 + 6\sqrt 3 \) là nghiệm. Tìm nghiệm còn lại.

Phân tích đa thức thành nhân tử: x²(x⁴ – 1)(x² + 2) + 1

Phân tích đa thức thành nhân tử: x² – 3xy – 10y²

Giải phương trình \({x^2} - 6x + 2 = 2\left( {2 - x} \right)\sqrt {2x - 1} \)

Tính số đo của góc x và góc y trong hình 9, biết 2x = 3y

Giải hệ phương trình \(\left\{ \begin{array}{l}x + y + xy + 1 = 0\\{x^2} + {y^2} - x - y = 22\end{array} \right.\)

Cho x + y + z = 1. Chứng minh giá trị biểu thức sau không phụ thuộc vào giá trị của biến, \(P = \frac{{{{\left( {x + y} \right)}^2}}}{{xy + z}}.\frac{{{{\left( {y + z} \right)}^2}}}{{yz + x}}.\frac{{{{\left( {x + z} \right)}^2}}}{{zx + y}}\)

Giải hệ phương trình: \(\left\{ \begin{array}{l}x + y + z = 1\\{x^4} + {y^4} + {z^4} = xyz\end{array} \right.\)

Tìm số hữu tỉ x, y biết: x + y = 3(x - y) = \(\frac{{2x}}{y}\)

Tìm giá trị nhỏ nhất của biểu thức A = x(x + 1)(x + 2)(x + 3)

Tìm các số nguyên x sao cho x(x – 1)(x – 7)(x – 8) là số chính phương

Tìm x biết: \(\frac{x}{{4,45}} - 2 = 1,7\)

Tìm x, y, z biết: \(\frac{x}{4} = \frac{{ - 9}}{y} = \frac{z}{8} = \frac{{ - 24}}{{32}}\)

Thu gọn S = x⁰ + x¹ + x² + x³ + … + xⁿ

Giải phương trình: x² + 7x – 18 = 0

Giải phương trình nghiệm nguyên x² + x + 1 = 2xy + y

Khai triển hằng đẳng thức x² – y²

Cho phương trình x² − 2(m + 1)x + m² = 0. Tìm m để phương trình có đúng một nghiệm.

Phân tích đa thức thành nhân tử x² - y² - 4x - 2y + 3

Giải hệ phương trình: \(\left\{ \begin{array}{l}{x^2} - {y^2} = 4x - 2y - 3\\{x^2} + {y^2} = 5\end{array} \right.\)

Tìm x, y là các số nguyên tố sao cho x² + 3xy + y² là số chính phương

Chứng minh rằng nếu x, y là hai số nguyên dương thoả mãn x² + 4xy - 8y²- 4y + 1= 0 thì 2y - x là số chính phương

Tìm nghiệm nguyên của phương trình: x² + xy + y² = x – y

Giải hệ phương trình \(\left\{ \begin{array}{l}{x^2} + {y^2} + 2\left( {xy + 3x - y} \right) = 0\\{x^2} + {y^2} + 4x - 2y = 0\end{array} \right.\)

Giải hệ phương trình \(\left\{ \begin{array}{l}{x^2} + {y^2} + 4x + 2y = 0\\{x^2} + 7{y^2} - 4xy + 6y = 13\end{array} \right.\)

Trên tập hợp Z các số nguyên. Chứng minh rằng x² + y² chia hết cho 5 khi và chỉ khi x và y đồng thời chia hết cho 5

Cho x² + y² – xy = 3; và x + y = \[\frac{2}{{{x^2} - xy + {y^2}}}\]. Chứng minh rằng x³ + y³ = 2

Tìm nghiệm nguyên dương của phương trình: x² + y² + z² + xyz = 20

Tìm các số nguyên x, y, z thỏa mãn: x² + y² + z² + 14 = 2x + 4y + 6z

Giải hệ phương trình \(\left\{ \begin{array}{l}{x^2} + x + {y^2} + y = 18\\xy\left( {x + 1} \right)\left( {y + 1} \right) = 72\end{array} \right.\)

Cho phương trình x² + (m – 4)x – m + 3 = 0, m là tham số

Tìm m để phương trình nhận \(x = 5 + 6\sqrt 3 \) là nghiệm. Tìm nghiệm còn lại.

Phân tích đa thức thành nhân tử: x²(x⁴ – 1)(x² + 2) + 1

Phân tích đa thức thành nhân tử: x² – 3xy – 10y²

Giải phương trình \({x^2} - 6x + 2 = 2\left( {2 - x} \right)\sqrt {2x - 1} \)

Tìm cặp số nguyên x, y thỏa mãn x² – x(y + 5) = –4y – 9

Giải phương trình vô tỉ: \({x^2} - x - 1000\sqrt {1 + 8000x} = 1000\)

Tìm x biết: x³ – 7x – 6 = 0

Giải phương trình \(\sqrt {x + 3} + \sqrt {3x + 1} = 2\sqrt x + \sqrt {2x + 2} \)

Giải hệ phương trình \(\left\{ \begin{array}{l}{x^3} + 3x{y^2} = 6xy - 3x - 49\\{x^2} - 8xy + {y^2} = 10y - 25x - 9\end{array} \right.\)

Biết x, y, z là những số nguyên thỏa mãn x³ + y³ + z³ chia hết cho 27. Chứng minh rằng hoặc cả ba số x, y, z cùng chia hết cho 3, hoặc 2 trong ba số có tổng chia hết cho 9.

Tìm tất cả số nguyên tố p để phương trình x³ + y³ - 3xy + 1 = p có nghiệm nguyên dương.

Giải hệ phương trình: \(\left\{ \begin{array}{l}{x^3}\left( {{y^2} + 3y + 3} \right) = 3{y^2}\\{y^3}\left( {{z^2} + 3z + 3} \right) = 3{z^2}\\{z^3}\left( {{x^2} + 3x + 3} \right) = 3{x^2}\end{array} \right.\)

Giải hệ phương trình: \(\left\{ \begin{array}{l}{x^3} = 3x + 4 + y\\{y^3} = 3y + z - 6\\{z^3} = 12z - x + 18\end{array} \right.\)

Giải hệ phương trình: \(\left\{ \begin{array}{l}{x^3} - 9{z^2} + 27z - 27 = 0\\{y^3} - 9{x^2} + 27x - 27 = 0\\{z^3} - 9{y^2} + 27y - 27 = 0\end{array} \right.\)

Phân tích đa thức thành nhân tử: x⁴ + 2x³ + x² + x + 1

Cho các biểu thức A= x⁴ + x; B = x⁴ + x + 1. Tìm số tự nhiên x để A và B đều là số nguyên tố.

Giải phương trình \({x^4} + 4{x^3} + 6{x^2} + 4x + \sqrt {{x^2} + 2x + 10} = 2\)

Cho đa thức A(x) = x⁴ + 5x³ – 6x + 2x² + 10x – 5x³

B(x) = x⁴ – 2x³ + 2x² + 6x³ + 1

a) Thu gọn hai đa thức trên và tính M(x) = A(x) – B(x)

b) Tìm nghiệm của M(x) = 0

Phân tích đa thức thành nhân tử: x⁶ + x³ – x² – 1

Phân tích đa thức thành nhân tử: x⁷ + x⁵ + 1

Tìm các số nguyên dương x, y thỏa mãn \(x = \sqrt {2x\left( {x - y} \right) + 2y - x + 2} \)

Tìm \(\frac{{x - 1}}{2} = \frac{8}{{x - 1}}\)

Tìm x biết: \(\frac{{x - 1}}{{2011}} + \frac{{x - 2}}{{2010}} - \frac{{x - 3}}{{2009}} = \frac{{x - 4}}{{2008}}\)

Tìm x biết: \(\frac{x}{{ - 2}} = \frac{{ - 8}}{x}\)

Tìm các số nguyên tố x, y sao cho x² + 45 = y²

Tìm các số nguyên x sao cho: 2x - 1 chia hết cho x - 3

Tìm x ∈ ℕ biết x + 3 chia hết cho x – 1

Tìm x nguyên biết x – 3 chia hết cho 2x

Tính giá trị của biểu thức: T = (3x + 5y).(x - y) khi x = -15; y = -10

Tìm hàm số y = x² + bx + c biết hàm số có đỉnh I(-2;-1)

Cho tam giác ABC, M thuộc tam giác đó. AM, BM, CM cắt BC, CA, AB tại P, R, Q. Chứng minh:

a) MA.BC + MB.CA + MC .AB ≥ 4S_ABC

b) Xác định vị trí của M để diện tích tam giác PQR lớn nhất

XIX là số mấy?

Thế kỉ XV bắt đầu từ năm nào đến hết năm nào?

Tìm cặp số nguyên x, y sao cho x – y – 2xy = 3

Giải phương trình nghiệm nguyên dương: xy + yz + zx = xyz + 2

Giải hệ phương trình: \(\left\{ \begin{array}{l}xy\left( {3x + y} \right) = 4\\7{x^3} + 11 = 3\left( {x + y} \right)\left( {x + y + 1} \right)\end{array} \right.\)

Phân tích đa thức thành nhân tử: xy(x + y) + yz(y + z) + xz(x + z) + 3xyz

Giải hệ phương trình: \(\left\{ \begin{array}{l}x{y^2} - 3{x^3}y - 4y{x^2} - y + 3{x^2} = 0\\3{x^2}y - {y^2} + 3xy + 1 = 0\end{array} \right.\)

Tìm các số tự nhiên x, y, z khác 0 biết xyz = 4(x + y + z)

Tìm x, y, z nguyên dương biết xyz = x + y + z + 9

Tính \(\int\limits_0^{\frac{\pi }{4}} {\frac{{3{{\sin }^2}x - 4{{\cos }^2}x}}{{{{\cos }^2}x}}dx} \)