10000 câu trắc nghiệm tổng hợp môn Toán 2025 mới nhất (có đáp án) - Phần 15

Cho tam giác ABD vuông tại A có AB < AD. Gọi M là trung điểm của BD. Lấy C sao cho M là trung điểm của AC.

a) Chứng minh ABCD là hình chữ nhật.

b) Trên tia đối DA lấy E sao cho DA = DE. Gọi I là trung điểm của CD. Chứng minh IB = IE.

c) Kẻ AH vuông góc với BD. Lấy K sao cho H là trung điểm của AK. Chứng minh BDCK là hình thang cân.

Cho B = 1.2 + 2.3 + 3.4 + …..+ 31.32 + 32.33. Chứng tỏ rằng B ⋮ 34.

Cho biểu thức E = \(2024! + \frac{{2024!}}{2} + \frac{{2024!}}{3} + ........ + \frac{{2024!}}{{2024}}\). Chứng minh E chia hết cho 2025.

Cho 6 số 4; 7; 0; 1; 2. Có thể lập được bao nhiêu số chẵn có ba chữ số từ 6 chữ số trên.?

Điền vào chỗ chấm: Chữ số thứ 99 của dãy số 2, 4, 6, 8,……..,100.

Cho đoạn thẳng AB = 6 cm, biết tập hợp điểm M thoả mãn MA = 2MB. Tính MB?

Cho hai phân số \(\frac{7}{9}\) và \(\frac{5}{{11}}\). Tìm phân số \(\frac{a}{b}\) sao cho đem mỗi phân số đã cho trừ đi \(\frac{a}{b}\) thì được phân số mới có tỉ số là 5.

Cho hai tập hợp A =(m −1; 8) và B = (2; +∞). Tìm tất cả các giá trị của số thực m để A khác tập rộng A\ B = ∅.

Cho hai tập hợp A = [−4; 2] và B = [−8; a + 2]. Tìm tất cả các giá trị của số thực a để A giao B có vô số phần tử.

Cho hàm số y = 2x² – 3(m + 1)x + m² + 3m – 2, m là tham số. Tìm tất cả các giá trị của để giá trị nhỏ nhất của hàm số là lớn nhất.

Cho hình chữ nhật MNPQ có O là giao điểm hai đường chéo. Biết  MN = 3 cm; MO = 2,5 cm . tính độ dài của PO, NQ.

Cho hình bình hành ABCD có diện tích 180 cm² chu vi là 58 cm và cạnh AD và AB là hai số tự nhiên liên tiếp. Đoạn thẳng MN chia hình bình hành ABCD thành hai hình bình hành AMND và MBCN, biết MB hơn AM là 5cm. Tính:

a) Chu vi hình bình hành MBCN.

b) Diện tích hình bình hành AMND.

Cho hình bình hành ABCD. Gọi E, F là hai điểm thỏa mãn \(\overrightarrow {BE} = \frac{1}{3}\overrightarrow {BC} \), \(\overrightarrow {BF} = \frac{1}{4}\overrightarrow {BD} \) khi đó \(\overrightarrow {AE} = k\overrightarrow {AF} \). Tìm k.

Cho hình bình hành ABCD, biết cos \(\widehat {BAD} = \frac{1}{3}\). Tính cos \(\widehat {ABC}\).

Tính diện tích xung quanh của hình hộp chữ nhật có chiều dài \(\frac{5}{6}\)m, chiều rộng là \(\frac{2}{3}\)m và chiều cao là \(\frac{1}{4}\)m.

Cho hình thang ABCD có \(\widehat A = \widehat B\) = 90°, BC = 2AD = 2AB .Gọi M là điểm nằm trên đáy nhỏ AD, kẻ Mx vuông góc MB cắt CD tại N. Chứng minh  BM = MN.

Cho Hình bên , biết rằng mn // pq. Tính số đo các góc mHK, vHn.

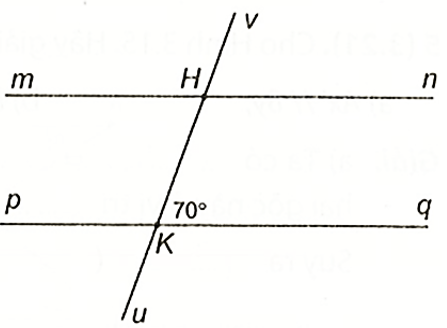
Cho hình vẽ có \({\widehat B_3}\)= 80°.

a) Tính số đo \(\widehat {{B_1}}\) và \({\widehat C_2}\).

b) Vẽ tia phân giác Ct của góc \(\widehat {BCy}\), tia Ct cắt tia xx’ ở E. So sánh góc BCE và góc BEC.

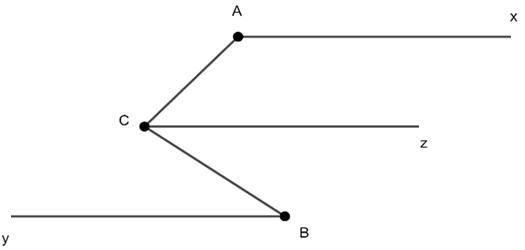
Cho hình vẽ bên. Biết:

\(\widehat {xAC}\)= 120°; \(\widehat {ACB}\)= 80°; \(\widehat {CBy}\)= 20°. Chứng minh Ax // By

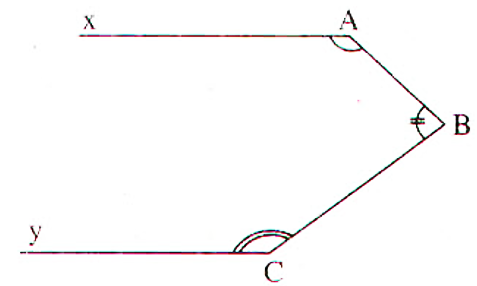
Cho hình vẽ sau. Biết \(\widehat A + \widehat B + \widehat C = 360^\circ .\) Chứng minh Bx // Cy.

Cho khoảng A = (−1; m + 2) và nửa khoảng B = [3m – 4; 14] (m là tham số). Gọi S là tập hợp tất cả các số nguyên m sao cho A∪B = (−1;14). Tính tổng các phần tử của tập hợp S.

Cho hình bình hành ABCD có chu vi là 98 cm. Nếu giảm độ dài cạnh AB là 14 cm, tăng độ dài cạnh AD thêm 7 cm được hình thoi AEGH. Tính độ dài cạnh hình thoi và các cạnh hình bình hành.

Cho một phân số tối giản, biết rằng nếu cộng thêm ba lần mẫu số vào tử số và giữ nguyên mẫu số thì giá trị của phân số sẽ tăng lên 6 lần. Tìm phân số đó.

Cho một phép trừ hai số mà tổng của số bị trừ, số trừ và hiệu số bằng 2020. Hiệu số lớn hơn số trừ là 165. Hãy tìm số bị trừ và số trừ của phép tính đó.

Cho các đa thức P(x) = x³ + ax² + bx + c và Q(x) = x² + 2016x + 2017 thỏa mãn P(x) = 0 có 3 nghiệm phân biệt và Q(x) = 0 vô nghiệm.

Chứng minh: P(2017) > 1008⁶.

Cho phân số \(\frac{{19}}{{89}}\). Tìm số tự nhiên a biết rằng khi thêm a và tử số và bớt a ở mẫu số thì được phân số là \(\frac{2}{7}\).

Cho phân số P = \(\frac{{6n + 5}}{{3n + 2}}\). Chứng minh P là phân số tối giản.

Giải phương trình \[\frac{{\sin 3x}}{{\cos (3x - 1)}} = 0.\]

Cho phương trình x² + 3x + m – 4 = 0. Giải phương trình tại m = 4.

Cho phương trình x² – 2x + k² – 3k – 9 = 0 với k là tham số. Khi đó phương trình đã cho có Q = \(\sqrt {{x_1}^2 + {x_2} - {x_1} + k + 10} + \sqrt {{x_1}^2 - 2{x_2} + 1} \).

Cho phương trình x³ + ax² + bx + 1 = 0. Biết rằng a, b là các số hữu tỉ và \(1 + \sqrt 2 \) là nghiệm của phương trình. Tìm a và b.

Cho tam giác ABC có BC = 8 cm , AB = 3 cm , \(\widehat B\) = 60°. Độ dài cạnh AC là bao nhiêu?

Cho tam giác ABC có đường cao AH biết AB = 6a, AC = 8a và BC =10a. Tính chiều cao AH.

Cho tam giác ABC gọi K là trung điểm BC I là trung điểm AC; AK cắt BI tại G trên ab lấy N sao cho AN=\(\frac{1}{3}\)AB.

 a) G là trọng tâm tam giác ABC

 b) Chứng minh \[\frac{{BN}}{{BA}} = \frac{{BG}}{{BI}};{\rm{ }}\frac{{AN}}{{NB}} = \frac{{IG}}{{GB}}\].

c) Từ G kẻ đường thẳng song song với BC cắt AB tại H, biết NI = 8 cm. Tính CH.

Cho tam giác ABC thỏa mãn \(\frac{{{a^3} + {b^3} - {c^3}}}{{a + b - c}} = {c^2}\). Chứng minh \(\widehat C\)= 60°.

Cho tam giác ABC vuông tại A có BC = 8 cm, biết sin B = \(\frac{2}{5}\). Tính độ dài AC.

Cho tam giác ABC vuông tại A có AB = 21 cm; BC = 35 cm.

a) Giải tam giác vuông ABC.

b) Kẻ AH ⊥ BC. Tính AH, HB.

Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 7 cm; BC = 25 cm.

a) Tính AH, BH, HC.

b) Kẻ HM ⊥ AB, HN⊥ AC. Tính diện tích tứ giác BMNC.

Cho tam giác ABC vuông tại A có AB = 3a, AC = 4a. Tính độ dài vectơ BC.

Cho tập hợp A= {1; 3; 5;…; 2019}. Tính số phân tử của tập hợp đó.

Chú Hùng cửa một tấm gỗ dạng hình chữ nhật để lấy ra một hình vuông như hình dưới đây. Tính diện tích phần gỗ bỏ đi.

Tìm số tận cùng của 8²⁰²¹

Một vườn hoa hình chữ nhật có chu vi là 120 m. Chiều rộng bằng \(\frac{5}{7}\) chiều dài.

a) Tính chiều dài và chiều rộng vườn hoa đó.

b) Người ta sử dụng \(\frac{1}{{25}}\) diện tích vườn hoa để làm lối đi. Hỏi diện tích lối đi là bao nhiêu?

Công thức chu vi đáy hình hộp chữ nhật.

Cho hình vẽ dưới đây. Chứng minh đường thẳng ab song song với cd.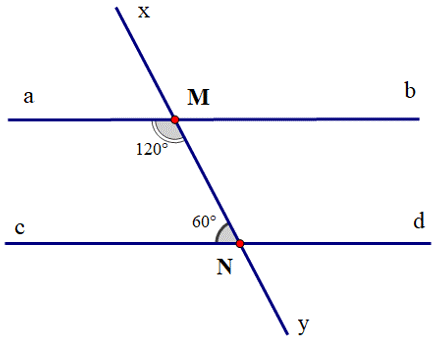

Chứng minh 2113²⁰⁰⁰  − 2111²⁰⁰⁰ chia hết cho 2 và 5.

Chứng minh 2999²⁰¹³ – 1998²⁰¹² – 1003²⁰¹³ chia hết cho 2 và 5

Cách chứng minh biểu thức không phụ thuộc vào biến

Tính a² − b² = ?

Với các số thực dương a, b, c thỏa mãn a² + b² + c² + 2ab = 1. Tìm giá trị lớn nhất của P = ab + bc + ca – abc.

Cho a, b, c là các số nguyên khác 0, a khác c sao cho \({a^2} + \frac{{{a^2}}}{{{b^2} + {c^2}}} = \frac{a}{c}\).

Chứng minh a² + b² + c² không phải số nguyên tố?

Chứng minh a² − b² = (a – b) (a + b)

Tính a² − b² = ?

Chứng minh a³ + b³ + c³ = 3 abc thì a = b = c hoặc a + b + c = 0

Cho a và b là hai số thực phân biệt thỏa mãn a² + 4a = b² + 4a = 7.

a) Tính S = a + b.

b) Tính Q = a³ + b³.

Cho A = 2 + 2² + 2³ + …+2¹². Chứng minh A ⋮ 2.

Tính tỉ số \(\frac{A}{B}\) biết

\(A = \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ..... + \frac{1}{{2017}} + \frac{1}{{2018}} + \frac{1}{{2019}}\)

\(B = \frac{{2018}}{1} + \frac{{2017}}{2} + \frac{{2016}}{3} + ... + \frac{2}{{2017}} + \frac{1}{{2018}}\)

Cho A = 5 + 5² + 5³ +….+ 5²⁰¹⁹. Chứng minh 4A + 5 là một số chính phương?

Chứng minh A = 5ⁿ⁺² + 5ⁿ⁺¹ + 5ⁿ (n ∈ ℕ) chia hết cho 31.

Cho hai số tự nhiên a và b sao cho a.b = 1996¹⁹⁹⁵. Hỏi a + b có chia hết cho 1995 không?

Cho ΔABC vuông tại A có đường cao AH. Gọi D là trung điểm của AC; vẽ DE vuông góc với BC tại E. Chứng minh: EB² – EC² = AB².

Cho a, b, c > 0 thỏa mãn ab + bc + ca + abc = 4. Chứng minh  \(\sqrt {ab} + \sqrt {bc} + \sqrt {ca} \le 3\)

Tìm số tự nhiên có 3 chữ số abc biết \(\overline {abc} \) : 11 = a + b + c

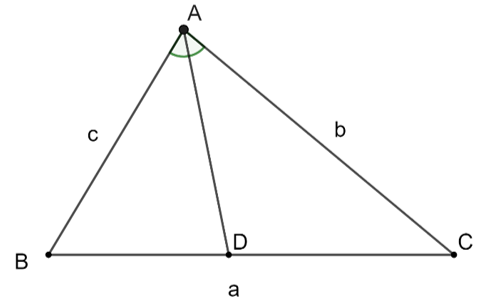
Cho tam giác ABC có AD là tia phân giác của \(\widehat {BAC}\).

Chứng minh: \(AD = \frac{{2bc.\cos \frac{A}{2}}}{{b + c}}\).

Anh Vinh đi ô tô từ thành phố Vũng Tàu đến thành phố Cần Thơ với vận tốc trung bình 50km/h. Khi từ thành phố Cần Thơ về thành phố Vũng Tàu , anh ấy chọn con đường khác dài hơn đường cũ 10 km, đi với vận tốc trung bình 60 km/h. Do đó, thời gian về ít hơn thời gian đi 40 phút. Tính quãng đường lúc đi từ Vũng Tàu đến thành phố Cần Thơ.

Cho số B = \({3^{n + 2}} - {2^{n + 2}} + {3^n} - {2^n}\) với n ∈ ℕ. Khi đó, chữ số tận cùng của biểu thức B là

Ba bạn An, Bình, Dũng cùng góp tiền mua 1 quả bóng. Bạn An góp \(\frac{1}{4}\) số tiền mua quả bóng. Bạn Bình góp \(\frac{3}{{10}}\) số tiền mua bóng, bạn Dũng góp nhiều hơn bạn Bình 3 000 đồng. Tính số tiền mỗi bạn góp?

Điền vào chỗ chấm: ba mươi hai đơn vị và mười sáu phần trăm đơn vị là ….

Bác Hùng có một mảnh vườn hình chữ nhật với lối đi có kích thức như hình vẽ dưới đây.

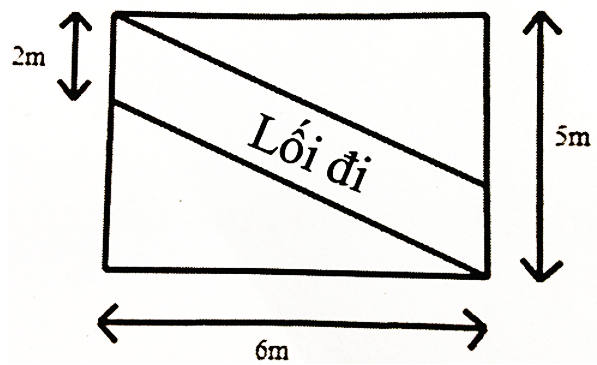
a) Tính diện tích của mảnh vườn hình chữ nhật.

b) Tính diện tích của lối đi.

c) Phần diện tích còn lại bác Hùng trải thảm cỏ với giá 170 000 đồng/m². Tính số tiền bác Hùng phải trả để trải thảm cỏ?

Bác Nam có một mảnh vườn hình chữ nhật với chiều dài 20 mét và chiều rộng 12 mét. Giữa mảnh vườn bác đào một cái ao hình vuông để nuôi cá có cạnh 8 mét, phần còn lại của mảnh vườn bác dùng để trồng rau.

a) Tính chu vi của mảnh vườn hình chữ nhật.

b) Tính diện tích trồng rau trên mảnh vườn của bác Nam.

Làm tròn các số thập phân sau đến hàng đơn vị (hay đến số tự nhiên gần nhất)

2,28 →……

3,73 →…….

7,02 →…..

6,53 →……

Cách giải bài toán thực tế về bất phương trình lớp 9?

Bạn An mỗi ngày tiết kiệm được 5 000 đồng ăn sáng để mua dụng cụ học tập hỗ trợ các bạn học sinh khó khăn. Sau 7 ngày bạn An mua được một bộ dụng cụ học tập nói trên và dư 2 000 đồng.

a) Hỏi một bộ dụng cụ học tập An mua có giá bao nhiêu?

b) Sau cơn bão Yagi tại miền Bắc nước ta bạn An nhận thấy các bạn học sinh ở đó đang rất cần thêm sự hỗ trợ và dự kiến cứ sau 7 ngày tiếp theo số dụng cụ học tập cần mua tăng gấp 3 lần số bộ dụng cụ học tập hiện có. Hãy viết biểu thức tính có sử dụng phép nâng lũy thừa biểu thị số bộ dụng cụ học tập bạn An cần mua sau bốn tuần đầu tiên thực hiện.

Bạn An đo được bán kính của một hình tròn là 5 ± 0,2 cm. Tuấn tính chu vi hình tròn là p = 31,4 cm. Hãy ước lượng sai số tuyệt đối của p, biết 3,141 < π < 3,142.

Bạn Mai có một cái bánh ngọt có dạng hình lăng trụ đứng tam giác, kích thước như sau.

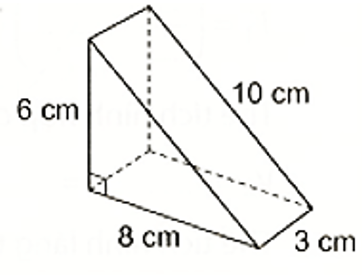
a) Tính thể tích cái bánh.

b) Nếu phải làm một chiếc hộp để cái bánh này thì diện tích vật liệu cần dùng là bao nhiêu (coi mép dán không đáng kể)?

Bạn Minh đã dùng bìa để làm một chiếc hộp hình chữ nhật có chiều dài 14 cm, chiều rộng 10 cm, chiều cao 8 cm. Tính diện tích bìa dùng để làm hộp, biết diện tích bìa làm mép dán là 70 cm² .

Gia đình An muốn xây dựng một bể chứa nước hình trụ có thể tích 150 m³. Đáy bể làm bằng bê tông giá 100 000 đồng/m². Phần thân làm bằng vật liệu chống thấm giá 90 000 đồng/m², nắp bằng nhôm giá 120 000 đồng/m². Hỏi tỷ lệ số giữa chiều cao bể và bán kính đáy là bao nhiêu để chi phí sản xuất bể đạt giá trị nhỏ nhất?

A. \(\frac{{31}}{{22}}\).

B. \(\frac{{22}}{{31}}\).

C. \(\frac{9}{{22}}\).

D. \(\frac{{22}}{9}\).

Bạn Nhi lên kế hoạch tự trồng rau tại nhà bằng những thùng xốp. Mỗi thùng có chiều rộng 50 cm, chiều dài 70 cm và chiều cao 30 cm. Ba của Nhi mua cho bạn 1,26m³ đất trồng cây?

a, Hỏi với lượng đất này, bạn Nhi trồng được bao nhiêu thùng xốp?

b, Khi đó khu vườn của bạn Nhi có diện tích bằng bao nhiêu?

Bảng số nguyên tố từ 1 đến 100

Tìm bội chung của 12, 15, 18?

Tìm bội chung của 220, 240, 300?

Tìm BCNN (10, 14, 16)

Biết rằng a công nhân làm trong b ngày. Tính xem b công nhân làm trong bao nhiêu ngày được a công cụ?

Tìm bội 12

Tìm bội chung của 15; 18 và 20.

Tìm bội chung của 8 và 15.

Tìm bội 100

Tìm bội 120

Tìm bội 13

Tìm bội 14

Tìm bội 4

Tính \(B = \frac{1}{2} + {\left( {\frac{1}{2}} \right)^2} + {\left( {\frac{1}{2}} \right)^3} + {\left( {\frac{1}{2}} \right)^4} + ..... + {\left( {\frac{1}{2}} \right)^{98}} + {\left( {\frac{1}{2}} \right)^{99}}\)

Cả phân xưởng A và phân xưởng B sản xuất được 325 dụng cụ . Nếu phân xưởng A tăng thêm 25 dụng cụ và số dụng cụ của phận xưởng B giảm đi 5% thì tổng số dụng cụ của hai phân xưởng là 341 . Hỏi phân xưởng B sản xuất được bao nhiêu dụng cụ ?

Số cặp số nguyên tố cùng nhau?

Các phép tính lũy thừa cơ bản?

Các số nguyên tố lớn hơn 3 có dạng như nào?

Tìm các số nguyên x để biểu thức sau có giá trị nguyên A = \(\frac{3}{{x - 1}}\).

Hãy kể tên các số tự nhiên bình phương nhỏ hơn 200?

Hãy kể tên các tháng có 30 ngày trong năm 2025.