10000 câu trắc nghiệm tổng hợp môn Toán 2025 mới nhất (có đáp án) - Phần 10

Cho ba số x, y, z thỏa mãn:

\(\frac{{19}}{{x + y}} + \frac{{19}}{{y + z}} + \frac{{19}}{{z + x}} = \frac{{7{\rm{x}}}}{{y + z}} + \frac{{7y}}{{z + x}} + \frac{{7{\rm{z}}}}{{x + y}} = \frac{{133}}{{10}}\)

Tính M = x + y + z

Cho 30 điểm trong đó có đúng 5 điểm thẳng hàng (ngoài ra không có 3 điểm nào thẳng hàng). Qua 2 điểm ta vẽ được 1 đường thẳng. Hỏi có tất cả bao nhiêu đường thẳng?

Cho \(\frac{{4{\rm{a}} - 3b}}{{4c - 3{\rm{d}}}} = \frac{{4{\rm{a}} + 3b}}{{4c + 3{\rm{d}}}}\). Chứng minh rằng \(\frac{a}{b} = \frac{c}{d}\)

Cho A = 7³ + 7⁴+ 7⁵ + 7⁶ +….+7⁹⁸. Chứng tỏ A chia hết cho 8.

Cho a + b = 2. Tìm GTNN của biểu thức A = a² + b²

Tìm các số a, b, c biết rằng: 4a² + 2b² + 2c² + 4ab - 2bc + 2b – 10c + 17 ≤ 0

Cho a + b = 1. Tính a³ + b³ + 3ab

Chứng minh biểu thức luôn dương A = 25x² – 20x + 7

Chứng minh rằng nếu a, b, c là các số khác 0 thỏa mãn:

\(\frac{{ab + ac}}{2} = \frac{{ba + bc}}{3} = \frac{{ca + cb}}{4}\) thì \(\frac{a}{3} = \frac{b}{5} = \frac{c}{{15}}\).

Chứng minh rằng \(\frac{a}{{a + b}} = \frac{b}{{b + c}} + \frac{c}{{c + a}}\) không là số nguyên.

Cho \(\frac{a}{b} = \frac{c}{d}\). Chứng minh rằng: \(\frac{{7{a^2} + 3ab}}{{11{a^2} - 8{b^2}}} = \frac{{7{c^2} + 3cd}}{{11{c^2} - 8{d^2}}}\)

Chứng minh rằng trong các số có dạng 20142014...2014, có tồn tại số chia hết cho 2013.

Cho tam giác ABC có AB = AC, kẻ BD vuông góc AC, CE vuông góc AB (D thuộc AC, E thuộc AB). Gọi O là giao điểm của BD và CE. Chứng minh rằng tam giác OEB = tam giác ODC.

Chứng minh rằng tích của 3 số chẵn liên tiếp cho hết cho 8.

Chứng minh rằng đa thức x² + x + 1 không có nghiệm

Cho biểu thức \(B = \frac{1}{{{5^2}}} + \frac{1}{{{6^2}}} + \frac{1}{{{7^2}}} + ... + \frac{1}{{{{100}^2}}}\). Chứng tỏ rằng \(\frac{1}{6} < B < \frac{1}{4}\)

Cho ba số a, b, c khác nhau. Chứng minh rằng:

\(\frac{{b - c}}{{\left( {a - b} \right)\left( {a - c} \right)}} + \frac{{c - a}}{{\left( {b - c} \right)\left( {b - a} \right)}} + \frac{{a - b}}{{\left( {c - a} \right).\left( {c - b} \right)}} = \frac{2}{{a - b}} + \frac{2}{{b - c}} + \frac{2}{{c - a}}\).

Cho a² – ab + b² chia hết cho 9. Chứng minh rằng: a, b chia hết cho 3.

Có bao nhiêu số có 3 chữ số không chứa số 0.

Có bao nhiêu số là bội của 4 từ 14 đến 199

Có thể tìm dược 2025 số tự nhiên liên tiếp là hợp số không

Để hoàn thành xong một công việc cần 20 người làm trong 6 giờ. Hỏi muốn hoàn thành xong công việc đó trong 4 giờ thì cần bao nhiêu người?

Để lát gạch nền một căn phòng có diện tích 30m², người ta sử dụng một loại gạch có kích thước như nhau, biết diện tích mỗi viên gạch là 0,25m². Hãy tính tổng số viên gạch đủ để lát nền căn phòng đó.

Để trang trí lên một bức tường hình chữ nhật kích  thước 3m ´ 4m trong một căn phòng, bạn Hoa vẽ lên tường một hình như sau: Trên mỗi cạnh của hình lục giác đều có cạnh bằng 2dm, vẽ một cánh hoa hình parabol, đỉnh của parabol cách cạnh 3 dm và nằm phía ngoài hình lục giác đều, đường parabol đó đi qua hai đầu mút của mỗi cạnh (tham khảo hình vẽ bên).

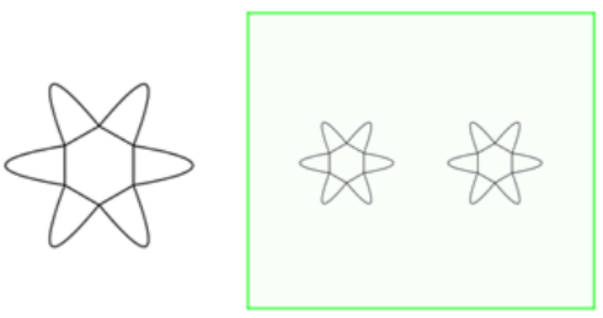
Hỏi bạn Hoa có thể vẽ tối đa bao nhiêu hình có cùng kích thước trên lên bức tường cần trang trí?

Điền các số 0,3; 0,7 và 1 vào chỗ trống để có biểu thức đúng

........... ´ (...........+..........) = ...........

Điền số vào ô trống sao cho 3 ô liên tiếp bất kì có tổng là 10 đơn vị:

Tính diện tích bông hoa được tô màu trong hình vẽ sau, biết hình vuông ABCD có độ dài cạnh là 4 cm.

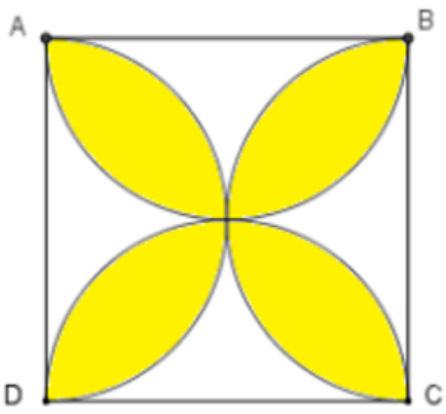
Diện tích hình vuông ABCD là 8cm². Tính diện tích hình tròn (xem hình vẽ)

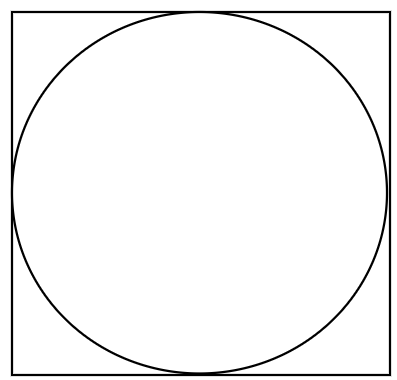
Một tấm gỗ hình chữ nhật có chu vi là 36 dm, chiều dài của tấm gỗ hơn chiều rộng 6dm. Tính diện tích tấm gỗ đó.

Hai bên sông A và B cách nhau 200 km. Một thuyền máy đi xuôi dòng từ A đến B với vận tốc 40 km/h. Cùng lúc đó, một thuyền máy đi ngược dòng với vận tốc 55 km/h và xuất phát cách B 10 km về phía A. Vận tốc dòng nước là 15 km/h. Hỏi sau bao lâu thì hai thuyền máy gặp nhau.

Viết phân số \(\frac{3}{4};\frac{5}{6};\frac{1}{3}\) theo thứ tự từ bé đến lớn

Hiệu của hai số là 45. Số thứ nhất bằng \(\frac{7}{2}\)số thứ hai. Tìm hai số đó.

Cho tam giác ABC có diện tích là 200 cm². Trên đáy BC lấy điểm M sao cho MB = 3MC. Tính diện tích tam giác ABM.

Hình thang ABCD có AB//CD, BD là đường cao của hình thang, \(\widehat A + \widehat C = 90^\circ \),   AB = 1 cm, CD = 3 cm. Tính AD, BC

Kết quả giới hạn \(\mathop {\lim }\limits_{x \to  - \infty } \left( {\sqrt {4{x^2} + x}  + 2x - 1} \right)\).

Kết quả giới hạn \(\mathop {\lim }\limits_{x \to  - \infty } \left( {\sqrt {4{x^2} + x}  + 2x - 1} \right)\).

Khi nhân một số tự nhiên với 103 do lúng túng, bạn Huệ đã viết thiếu chữ số 0 nên đã làm cho kết quả giảm 37080. Em hãy giúp bạn tìm tích đúng của phép tính.

Khi nhân một số tự nhiên với 142 do lúng túng bạn Lan đã viết lộn thừa số thứ 2 nên đã làm cho kết quả tăng 27255. Em hãy tìm tích đúng của phép tính.

Làm tròn 51 259 617 đến hàng trăm nghìn được:

Lớp 6A có \(\frac{2}{3}\) số học sinh thích bóng đá, \(\frac{5}{{12}}\) số học sinh thích bóng bàn, \(\frac{{13}}{{15}}\) số học sinh thích bóng chuyền. Hỏi môn bóng nào được nhiều bạn của lớp yêu thích nhất?

Lúc đầu bác Ngân mua 6 kg gạo hết 90 000 đồng, sau đó bác mua thêm 5 kg gạo nữa. Hỏi bác Ngân mua gạo hết tất cả bao nhiêu tiền? (Giá tiền mỗi kg gạo không đổi)

Tính nhanh: \(M = \frac{{1 + 2 + {2^2} + {2^3} + ... + {2^{2012}}}}{{{2^{2014}} - 2}}\)

Người ta lát một căn phòng hình vuông có cạnh 9m bằng những mảnh gỗ hình chữ nhật có chiều dài bằng 60 cm, chiều rộng 30 cm. Hỏi cần bao nhiêu mảnh gỗ để lát kín sàn căn phòng đó?

Tìm min của C = (2x + 1)(x + 2)(x + 3)(2x – 1)

Một bảng chỉ đường hình tròn có đường kính 60cm. Diện tích phần mũi tên chỉ đường trên biển báo bằng \(\frac{1}{5}\) diện tích biển báo. Tính phần diện tích còn lại của biển báo đó.

Diện tích hình chữ nhật là \(\frac{5}{8}\) m². Chiều dài là \(\frac{7}{8}\)m. Tính chu vi hình chữ nhật đó.

Một kho chứa 3 tấn gạo ngày thứ nhất xuất 800 kg gạo. Số gạo xuất trong ngày thứ hai bằng \(\frac{3}{2}\) số gạo xuất trong ngày đầu. Hỏi ngày thứ ba kho xuất bao nhiêu tấn gạo?

Một khu đất hình thang có độ dài đáy bé 40 m, đáy lớn gấp rưỡi đáy bé. Chiều cao bằng \(\frac{1}{2}\) tổng độ dài 2 đáy. Trên khu đất đó người ta dành 50% diện tích để xây nhà, 30% diện tích để làm vườn, phần còn lại để trồng hoa. Tính diện tích đất để xây nhà, làm vườn, trồng hoa.

Một mảnh vườn hình chữ nhật có nửa chu vi là 17 m. Chiều rộng kém chiều dài 5 m. Tính diện tích mảnh vườn đó.

Một hình tam giác có độ dài đáy là 1,5 dm và chiều cao bằng \(\frac{2}{3}\) cạnh đáy. Tính diện tích hình tam giác đó.

Một hình chữ nhật có chiều rộng 5 m, chiều dài gấp đôi chiều rộng. Tính chu vi hình chữ nhật.

Một mảnh đất hình thang có diện tích 420 m². Sau khi mở rộng đáy nhỏ 2m, đáy lớn 4 m thì diện tích tăng lên 42 m². Tính độ dài mỗi đáy mảnh đất, biết đáy lớn hơn đáy bé 8 m.

Một khu vườn hình chữ nhật có diện tích bằng 396 m². Nếu tăng chiều rộng thêm 4 m thì được khu đất hình vuông. Hỏi phải dùng bao nhiêu chiếc cọc để rào xung quanh khu vường đó. Biết rằng cọc nọ cách cọc kia 1 mét ở góc vườn, người ta để một lối đi rộng 2m và số đó các cạnh đều là số tự nhiên.

Một mảnh vườn hình chữ nhật có chiều rộng 90 m, chiều dài gấp 2 lần chiều rộng. Tính chu vi và diện tích mảnh vườn đó.

Một ngày 12 giờ bằng bao nhiêu giờ?

Một người mua 3 đôi giày với hình thức khuyến mãi như sau: Nếu bạn mua một đôi giày với mức giá thông thường, bạn sẽ được giá giảm 30% khi mua đôi thứ hai và mua một đôi thứ ba với một nửa giá ban đầu. Ban Khang đã trả 1 320 000 đồng cho 3 đôi giày. Giá ban đầu của một đôi giày là bao nhiêu?

Một người nông dân thả 1000 con cá giống vào hồ nuôi vừa mới đào. Biết rằng sau mỗi năm thì số lượng cá trong hồ tăng lên x lần so với lượng cá ban đầu và x không đổi. Bằng cách thay đổi kỹ thuật nuôi và thức căn cho cá. Hỏi sau hai năm để số cá trong hồ là 36000 con thì tốc độ tăng số lượng cá trong hồ x là bao nhiêu? Biết tốc độ tăng mỗi năm là không đổi.

Một nhân viên ở cửa hàng bán đồ ăn nhanh khi xếp số bánh nọt vào các túi thì thấy rằng nếu xếp mỗi túi 10 chiếc, 12 chiếc hoặc 15 chiếc đều vừa đủ. Tính số bánh ngọt của cửa hàng biết rằng số bánh ngọt trong khoảng 100 đến 150 chiếc.

Một thửa ruộng hình thang có đáy lớn là 130 m, đáy bé bằng \(\frac{4}{5}\) đáy lớn, chiều cao 4 m. Trung bình cứ 100 m² thu hoạch 65 kg thóc. Tính số kg thóc thu hoạch được trên thử ruộng đó?

1kg bằng bao nhiêu gam?

0 có phải là một số nguyên không?

3,12 đổi ra phân số bằng bao nhiêu?

số 0 có phải là số nguyên dương không?

số 0 có phải là số tự nhiên không?

Tính: (‒0,25)⁴.4⁴.

Tính tích:

\[\left( {1 + \frac{7}{9}} \right) \cdot \left( {1 + \frac{7}{{20}}} \right) \cdot \left( {1 + \frac{7}{{33}}} \right) \cdot .. \cdot \left( {1 + \frac{7}{{2900}}} \right)\].

Tìm x, biết:

\[\left( {\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ... + \frac{1}{{2014}}} \right) \cdot x = \frac{{2013}}{1} + \frac{{2012}}{2} + \frac{{2011}}{3} + ... + \frac{2}{{2012}} + \frac{1}{{2013}}\].

Tính nhanh:

(145 × 99 + 145) ‒ (143 × 102 ‒ 143).

Tính:

A = (‒2) + (‒59) ‒ (‒22) + 59.

Tính: \[\frac{{{2^{23}} + {\rm{ }}{2^{24}} + {\rm{ }}{2^{25}}}}{{{2^{18}} + {2^{19}} + {2^{20}}}}\].

Tính hợp lí:

\[\frac{{{2^3} \cdot {9^4} + {9^3} \cdot 45}}{{{9^2} \cdot 10 - {9^2}}}\].

Tìm x, biết: (2x ‒ 1)³ = 27.

Tìm tất cả các nghiệm nguyên của phương trình:

(3x ‒ 16y ‒24)² = 9x² + 16x + 32.

Tìm x:

(4x ‒ 3)⁴ = (4x ‒ 3)².

Tính:

\[\frac{{\left( { - \frac{5}{7} - \frac{7}{9} + \frac{9}{{11}} - \frac{{11}}{{13}}} \right) \cdot \left( {3 - \frac{3}{4}} \right)}}{{\left( {\frac{{10}}{{21}} + \frac{{14}}{{27}} - \frac{{18}}{{33}} + \frac{{22}}{{39}}} \right):\left( {2 - \frac{2}{3}} \right)}}\].

Tìm x, biết:

(5x + 1)² ‒ (5x + 3)(5x ‒ 3) = 30.

Tính tổng:

\[A = \frac{{38}}{{25}} + \frac{9}{{10}} - \frac{{11}}{{15}} + \frac{{13}}{{21}} - \frac{{15}}{{28}} + \frac{{17}}{{36}} - ... + \frac{{197}}{{4851}} - \frac{{199}}{{4950}}\].

Tìm a để: (a ‒ 3) chia hết cho (a ‒ 14).

Chứng minh rằng:

(a + b + c)³ = a³ + b³ + c³ + 3(a + b).(b + c).(c + a).

ho a, b, c ≥ 0 với a + b + c = 3 và \[P = \frac{{{a^2}}}{{a + 2{b^3}}} + \frac{{{b^2}}}{{b + 2{c^3}}} + \frac{{{c^2}}}{{c + 2{a^3}}}.\] Tìm GTNN của P.

Cho phương trình: (m² + 2m + 2)x² ‒ (m² ‒ 2m + 2)x ‒ 1 = 0.

Tìm GTLN và GTNN của S = x₁ + x₂ với x₁, x₂ là nghiệm của phương trình đã cho.

Cho hệ phương trình: \[\left\{ \begin{array}{l}\left( {m - 1} \right)x - \left( {m - 1} \right)y = m - 37\,\,\,\left( 1 \right)\\x + 2y = 3m + 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\]

a) Với m nào thì hệ phương trình có nghiệm duy nhất?

b) Tìm m để phương trình có nghiệm nguyên x, y và x + y bé nhất.

Tìm n thuộc ℤ sao cho n + 5 chia hết cho 2n ‒ 1.

Tìm các số tự nhiên x, y sao cho: (x + 1).(2y + 3) = 12.

Phân tích đa thức thành nhân tử:

(x + 1)(x + 2)(x + 3)(x + 4) ‒ 24.

Tìm x, biết: (x + 2)² ‒ x + 4 = 0.

Giải hệ phương trình: \[\left\{ \begin{array}{l}{\left( {x + y} \right)^2} = xy + 3y - 1\\x + y = \frac{{{x^2} + y + 1}}{{1 + {x^2}}}.\end{array} \right.\]

Giải phương trình: \[{\left( {{x^2} + 1} \right)^2} = 5 - x\sqrt {2{x^2} + 4} .\]

Tìm các số nguyên dương x, y thỏa mãn:

(x² + 4y² + 28)² = 17(x⁴ + y⁴ + 14y² + 49).

Cho số nguyên tố p. Giả sử x, y là số tự nhiên khác 0 thỏa mãn \[\frac{{{x^2} + p{y^2}}}{{xy}}\] là số tự nhiên. Chứng minh \[\frac{{{x^2} + p{y^2}}}{{xy}} = 1 + p\].

Phân tích đa thức thành nhân tử:

(x² + x ‒ 1)² + 4x² + 4x.

Giải hệ phương trình: \[\left\{ \begin{array}{l}2y({x^2} - {y^2}) = 3x\\x\left( {{x^2} + {y^2}} \right) = 10y\end{array} \right.\].

Tìm (x; y) thuộc ℤ thỏa mãn:

(x ‒ 2018)² = y⁴ ‒ 6y⁵ + 11y² ‒ 6y.

Tìm x, biết: (x ‒ 5)(x ‒ 7) = 0.

Phân tích đa thưc thành nhân tử:

(x + y)³ ‒ x(x + y)².

Tìm số tự nhiên n biết 3n + 7 chia hết cho n.

Cho hai tập hợp A, B thỏa mãn A∖B = {1; 2}, A ∩ B = {3; 4}. Khi đó số phần tử của tập hợp A là bao nhiêu?

Thực hiện phép tính:

[504 ‒ (5².8 + 70) : 3³ + 6] : 125.

Thực hiện phép tính:

\[\sqrt {3 - \sqrt 5 }  + \sqrt {3 + \sqrt 5 } \].