Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_TP Phú Thọ
22 câu hỏi
PHẦN I. TRẮC NGHIỆM (3,0 điểm)
Giá trị của \(\sqrt {2024} \) được làm tròn đến chữ số thập phân thứ hai là
\(44,98.\)
\(44,99.\)
\(45.\)
\(44.\)
Phương trình tích nào sau đây có nghiệm là \[x\, = \,3\,?\]
\[\left( {x\, + \,1} \right)\left( {2\, - \,x} \right)\, = \,0.\]
\[\left( {x\, + \,1} \right)\left( {x\, - \,1} \right)\, = \,0.\]
\[x\left( {x\, + \,3} \right)\, = \,0.\]
\[x\left( {x\, - \,3} \right)\, = \,0.\]
Nghiệm của bất phương trình \[4x - 2 > 2 + 2x\] là
\[x > 2.\]
\[x < 2.\]
\[x \ge 2.\]
\[x \le 2.\]
Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
\(2{x^2} - y = 3.\)
\(0x + 0y = 3.\)
\(x + {y^2} = 1.\)
\( - 2x + 4y = 2,5.\)
Cặp số \(\left( {1\,\,;\,\,2} \right)\) là nghiệm của hệ phương trình nào dưới đây?
\(\left\{ \begin{array}{l}x + y = - 1\\2x - y = 2\end{array} \right. \cdot \)
\[\left\{ \begin{array}{l}x + y = 3\\2x - y = 0\end{array} \right. \cdot \]
\[\left\{ \begin{array}{l}x + y = 3\\2x - y = 1\end{array} \right. \cdot \]
\[\left\{ \begin{array}{l}x + y = - 1\\2x + y = 0\end{array} \right. \cdot \]
Điểm nào sau đây thuộc đồ thị hàm số\(y = - 2{x^2}?\)
\[\left( { - 1\,;\,\,2} \right).\]
\[\left( {2\,;\,\, - 1} \right).\]
\[\left( { - 1\,;\,\, - 2} \right).\]
\(\left( { - 2\,;\,\, - 1} \right).\)
Cho phương trình bậc hai \(3{x^2} - 5x - 2 = 0\). Biết phương trình có một nghiệm \(x = 2.\) Nghiệm còn lại của phương trình là
\(\frac{{ - 2}}{3}.\)
\(\frac{{ - 1}}{3}.\)
\(\frac{{ - 5}}{3}.\)
\(\frac{{ - 4}}{3}.\)
Cho tam giác \[ABC\] vuông tại \[A,\,\,BC = a,\,\,\,AC = b,\,\,\,AB = c.\] Khẳng định nào dưới đây đúng?
\[b = a \cdot \cos B.\]
\[b = c \cdot \tan C.\]
\[b = a \cdot \sin B.\]
\(b = c \cdot \cot B.\)
Đặt một chiếc thang dài \(5{\rm{ m}}\) tạo mặt đất một góc bằng \(60^\circ .\) Khi đó chân thang cách tường
\(2,5{\rm{ m}}.\)
\(\frac{{5\sqrt 3 }}{2}{\rm{m}}.\)
\(5\sqrt 3 {\rm{ m}}.\)
\(\frac{{5\sqrt 3 }}{3}{\rm{ m}}.\)
Cho hình vẽ. Số đo của góc \[\widehat {AMB}\] là![Cho hình vẽ. Số đo của góc \[\widehat {AMB}\] là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/03/19-1741778194.png)
\[70^\circ .\]
\[220^\circ .\]
\[110^\circ .\]
\[55^\circ .\]
Cho tứ giác \(ABCD\) nội tiếp đường tròn biết \[\widehat A = 3\widehat C\]. Vậy số đo là
\(30^\circ .\)
\[45^\circ .\]
\[90^\circ .\]
\(135^\circ .\)
Một hộp đựng \(5\) quả cầu màu xanh, \(3\) quả cầu màu đỏ, \(7\) quả cầu màu trắng có cùng kích thước và khối lượng. Chọn ngẫu nhiên ra một quả cầu. Xác suất của biến cố “Quả cầu được chọn ra màu đỏ” là
\(\frac{1}{5} \cdot \)
\(\frac{2}{{15}} \cdot \)
\(\frac{3}{5} \cdot \)
\(\frac{7}{{15}} \cdot \)
1)Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 1\,\\x + y = 4\,\end{array} \right. \cdot \)
2) Tính giá trị biểu thức \(A = \sqrt {{{\left( {\sqrt 3 - 1} \right)}^2}} + \sqrt {12} .\)
3) Rút gọn biểu thức \[B = \left( {\frac{{\sqrt x }}{{\sqrt x + 2}} + \frac{2}{{\sqrt x - 2}}} \right):\frac{{x + 4}}{{\sqrt x + 2}}\], với \(x \ge 0\,,\,\,x \ne \pm 4.\)
1)a) Tìm \(a\) để đồ thị hàm số \(y = a{x^2}\)đi qua điểm \(M\left( {\sqrt 2 \,;{\rm{ }}2} \right).\)
b) Cho phương trình \[{x^2}\, - \,\left( {2m\, + \,1} \right)x\, + \,m\, = \,0\], \[m\] là tham số. Tìm các giá trị của \[m\] để phương trình có hai nghiệm \[{x_1}\,,\,{x_2}\] thoả mãn điều kiện \[\left( {{x_1} - 1} \right)\left( {{x_2} - 1} \right) \ge 19.\]
2)Giải bài toán sau bằng cách lập phương trình:
Một đội xe dự định trở \[75\] tấn hàng để ủng hộ đồng bào miền Trung, lúc sắp khởi hành nhận được ủng hộ thêm \[5\] tấn hàng và được bổ sung thêm \[5\] xe, do đó mỗi xe chở ít hơn dự định \[1\]tấn. Hỏi lúc đầu có bao nhiêu xe?
1)Chứng minh bốn điểm \(M,\,\,C,\,\,O,\,\,D\) cùng thuộc một đường tròn.
2)Chứng minh \(OM \bot CD\). Đoạn thẳng \[OM\] cắt đường tròn tại \[I,\] chứng minh \[I\] là tâm đường tròn nội tiếp tam giác \[MCD.\]
3)Đường thẳng qua \[O\] và vuông góc với \[OM\] cắt các tia \[MC,{\rm{ }}MD\] theo thứ tự tại \[P\] và \[Q.\]Tìm vị trí của điểm \[M\] trên đường thẳng \[d\] sao cho diện tích tam giác \[MPQ\] nhỏ nhất.
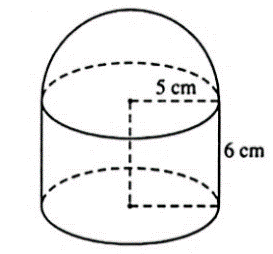
(0,5 điểm)Hình bên minh họa bộ phận lọc của một bình lọc nước. Bộ phần này gồm một hình trụ và một nửa hình cầu với kích thước ghi trên hình. Hãy tính diện tích mặt ngoài của bộ phận này.
(0,5 điểm)Giải phương trình \(8{x^2} - 21x + 49 = 11\sqrt {{x^3} - 4x + 15} .\)








