Đề thi minh họa môn Toán vào 10 tỉnh Đắk Lắk năm học 2025-2026
24 câu hỏi
I. PHẦN TRẮC NGHIỆM (4,0 điểm)
Giá trị nào dưới đây không phải là một nghiệm của bất phương trình \( - 3x + 4 < 0\)?
\(x = \frac{3}{2}\).
\(x = \frac{4}{3}\).
\(x = \frac{5}{3}\).
\(x = \frac{7}{3}\).
Cặp số nào sau đây là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{5x + 6y = 4}\\{4x - 9y = 17}\end{array}} \right.\)?
\(\left( { - 1;2} \right)\).
\(\left( { - 2;1} \right)\).
\(\left( {1; - 2} \right)\).
\(\left( {2; - 1} \right)\).
Phương trình nào sau đây không phải là phương trình bậc nhất hai ẩn?
\(2x + 3y = - 1\).
\(0x + 0y = 6\).
\( - 6x + y = 0\).
\( - 9y = 6\).
Phương trình nào sau đây là phương trình bậc hai một ẩn?
\({x^2} - 2\sqrt x + 1 = 0\).
\({x^2} + 1 = 0\).
\({x^3} - 2{x^2} + 1 = 0\).
\(2x + 1 = 0\).
Căn bậc hai số học của 144 là
72.
12 và \[ - 12\].
12.
\[ - 12\].
Với số thực \(a,\) khẳng định nào dưới đây đúng?
\(\sqrt {{a^2}} = a\).
\(\sqrt {{a^2}} = - a\).
\(\sqrt {{a^2}} = \pm a\).
\(\sqrt {{a^2}} = \left| a \right|.\)
Căn thức bậc ba của biểu thức \({\left( {1 - x} \right)^3}\) là
\(x - 1\).
\(1 - x\).
\(3\left( {1 - x} \right)\).
\(\sqrt[3]{{1 - x}}\).
Đồ thị của hàm số \(y = 2{x^2}\) có trục đối xứng là
Trục hoành.
Đường thẳng \(y = - x\).
Đường thẳng \(y = x\).
Trục tung.
Khẳng định nào dưới đây đúng?
Góc nội tiếp là góc có đỉnh nằm trong đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
Góc nội tiếp là góc có đỉnh nằm ngoài đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
Góc nội tiếp là góc có đỉnh trùng với tâm đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
Khẳng định nào sai trong các khẳng định dưới đây?
Đường tròn là hình có tâm đối xứng.
Tâm của đường tròn là tâm đối xứng của nó.
Mỗi đường thẳng đi qua tâm đường tròn là một trục đối xứng của nó.
Đường tròn là hình không có trục đối xứng.
Trong tam giác \(MNP\) vuông tại \(N,\) \(\sin \widehat {NPM}\) bằng
\(\frac{{MN}}{{MP}}\).
\(\frac{{NP}}{{MN}}\).
\(\frac{{MN}}{{NP}}\).
\(\frac{{MP}}{{NP}}\).
Cho tam giác \(ABC\) vuông ở \(A.\) Tỉ số nào dưới đây được dùng để tính \(\cot B?\)
\(\frac{{AC}}{{BC}}\).
\(\frac{{AC}}{{AB}}\).
\(\frac{{AB}}{{BC}}\).
\(\frac{{AB}}{{AC}}\).
Cho ba điểm \(A,\,\,B\) và \(C\) thuộc đường tròn \(\left( O \right)\) như hình bên. Góc nào dưới đây là góc ở tâm? 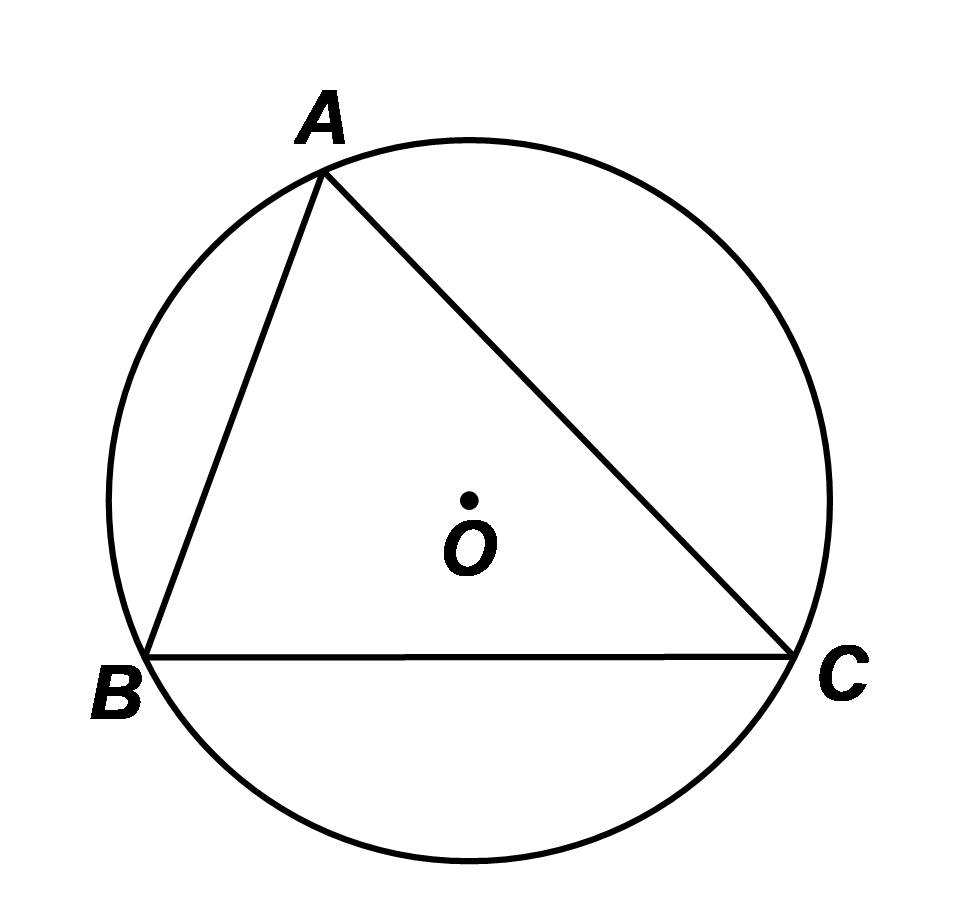
\(\widehat {BAC}\).
\(\widehat {OAB}\).
\(\widehat {BOA}\).
\(\widehat {BAO}\).
Trong các hình dưới đây, hình nào vẽ một tứ giác nội tiếp một đường tròn? 
Hình H1.
Hình H2.
Hình H3.
Hình H4.
Khi quay hình chữ nhật \(ABCD\) một vòng quanh cạnh \(AB\) ta được một hình trụ có bán kính đáy bằng độ dài đoạn thẳng nào đưới đây?
\(AD\).
\(AC\).
\(CD\).
\(AB\).
Diện tích mặt cầu có đường kính 10 cm bằng
\(100\pi \;{\rm{c}}{{\rm{m}}^2}\).
\(10\;{\rm{c}}{{\rm{m}}^2}\).
\(100\;{\rm{c}}{{\rm{m}}^2}\).
\(20\pi \;{\rm{c}}{{\rm{m}}^2}\).
1) Cho và Tính giá trị của biểu thức
2) Rút gọn các biểu thức sau
1) Cho phương trình \({x^2} - 5x + 3 = 0\). Chứng minh phương trình đã cho có 2 nghiệm phân biệt \({x_1};{x_2}\) và tính \(x_1^2 + x_2^2\).
2) Phong trào chơi môn thể thao Pickleball trong học sinh ngày càng tăng. Lớp 9A có 35 học sinh, trong đó chỉ có \(25\% \) của số học sinh nam và \(20\% \) của số học sinh nữ không chơi môn thể thao Pickleball. Biết tổng số học sinh nam và học sinh nữ không chơi môn thể thao Pickleball là 8 học sinh. Tính số học sinh nữ không chơi môn thể thao Pickleball.
1) Tính số đo cung lớn của đường tròn \(\left( {{O_1}} \right).\)
2) Tính độ dài dây cuaroa.
1) Biết rằng cả 3 thí sinh trong Câu lạc bộ Toán học đều có điểm thi không dưới 8. Chọn ngẫu nhiên 1 thí sinh của trường có điểm thi lớn hơn hoặc bằng 8. Tính xác suất để không có thí sinh của Câu lạc bộ Toán học nào được chọn.
2) Biết 3 thí sinh trong Câu lạc bộ Toán học gồm có 1 thí sinh nam và 2 thí sinh nữ. Trong buổi lễ tuyên dương khen thưởng 3 thí sinh của Câu lạc bộ Toán học, 3 thí sinh được sắp xếp ngẫu nhiên thành một hàng ngang để trao quà. Tính xác suất để 2 thí sinh nữ không đứng cạnh nhau.








