Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Bình Phước

2) Rút gọn biểu thức: $\mathrm{P}=\frac{{\mathrm{x}}^2-5}{\mathrm{x}+\sqrt{5}}$ , với $\mathrm{x}\ne -\sqrt{5}.$

1) Giải phương trình: \(\left( {2x + 3} \right)\left( {3x - 6} \right) = 0.\)

2) Không sử dụng máy tính hãy giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}5x - 2y = 8\\3x + 4y = 10.\end{array}\end{array}} \right.\)

3) Một sân bóng đá 7 người có chiều dài lớn hơn chiều rộng 20 m và có diện tích bằng \(1\,\,664\;\,{{\rm{m}}^2}.\) Tính chiều dài và chiều rộng của sân bóng đá đó.

1) Vẽ đồ thị của hàm số \(y = \frac{1}{2}{x^2}.\)

2) Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình: \({x^2} - 2x - 5 = 0.\) Không giải phương trình, tính giá trị của biểu thức \(S = x_1^3 + 9{x_2} + 7.\)

1) Hãy lập bảng tần số và bảng tần số tương đối số lỗi chính tả của học sinh.

2) Lấy ngẫu nhiên một học sinh trong lớp 9A, tính xác suất để học sinh này có số lỗi nhiều hơn 3.

1) Một bể nước hình trụ có bán kính đáy \(R = 1,2\;\;{\rm{m}}\) (tính từ tâm bể đến mép ngoài), bề dày của thành bể là \(b = 0,05\;\;{\rm{m,}}\) chiều cao lòng bể là \(h = 1,6\;\;{\rm{m}}\) (Hình 1). Tính dung tích của bể nước (kết quả làm tròn đến hàng phần trăm).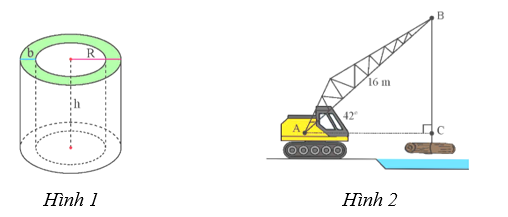                  

2) Một cần cẩu đang nâng một khối gỗ trên sông. Biết tay cẩu \(AB\) có chiều dài 16 m và nghiêng một góc \(42^\circ \) so với phương nằm ngang (Hình 2). Tính chiều dài \[BC\] của đoạn dây cáp (kết quả làm tròn đến hàng phần trăm).

1) Chứng minh tứ giác \(AEHF\) nội tiếp đường tròn tâm \(I.\)

2) Chứng minh \(FM\) vuông góc với \(FI.\)

3) Tiếp tuyến tại các điểm \(B\) và \(C\) của đường tròn ngoại tiếp tam giác \(ABC\) cắt nhau tại điểm \(N.\) Chứng minh rằng \(AN\) đi qua trung điểm của đoạn thẳng \(EF.\)