Đề thi minh họa Toán vào 10 năm học 2025 - 2026 Thái Bình
8 câu hỏi
Cho biểu thức \(A = \frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{2}{{\sqrt x + 2}} + \frac{{4\sqrt x + 2}}{{x + \sqrt x - 2}}\) và \(B = \frac{{\sqrt x - 1}}{{\sqrt x + 1}}\) với \(x \ge 0;\,\,x \ne 1.\)
1) Tính giá trị của biểu thức \[B\] khi \(x = 9.\)
2) Chứng minh rằng \(A = \frac{{\sqrt x + 2}}{{\sqrt x - 1}}.\)
3) Đặt \(T = 4 - \frac{3}{2}AB.\) Tìm các giá trị của \(x\) để biểu thức \(T\) nhận giá trị nguyên lớn nhất.
1) Gieo một con xúc xắc 20 lần liên tiếp. Kết quả mặt xuất hiện được ghi lại bởi bảng tần số:
Mặt xuất hiện | Mặt 1 chấm | Mặt 2 chấm | Mặt 3 chấm | Mặt 4 chấm | Mặt 5 chấm | Mặt 6 chấm |
Tần số | 2 | 4 | 2 | 5 | 4 | 3 |
Hãy cho biết đối tượng thống kê và kích thước của mẫu thống kê trên?
Biểu đồ bên biểu diễn tỷ lệ xếp loại kết quả học tập của học sinh lớp 9A. Tính xác suất của biến cố: “Chọn được học sinh có kết quả xếp loại học tập Khá hoặc Tốt” khi chọn ngẫu nhiên một học sinh của lớp đó.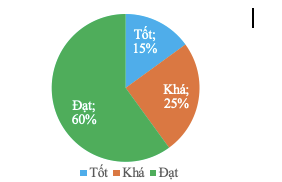
Một khối sắt hình cầu được làm bằng sắt nguyên chất, đặc ruột có giá trị diện tích mặt cầu (tính bằng m2) gấp 3 lần giá trị thể tích của khối cầu đó (tính bằng m3). Hỏi khối cầu sắt đó nặng bao nhiêu kilogram? (Biết rằng khối lượng riêng của sắt là \(7800\;{\rm{kg}}/{{\rm{m}}^3}\) và lấy \(\pi = 3,14).\)
Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Anh Khánh dự định mua một đôi giày thể thao và một chiếc vợt Pickleball với tổng số tiền theo giá niêm yết là 2,4 triệu đồng. Vì hôm đó cửa hàng có chương trình khuyến mãi giảm giá \(10\% \)cho đôi giày và \(15\% \) cho chiếc vợt nên anh Khánh đã mua thêm một chiếc vợt như vậy nữa để tặng bạn thân. Tổng số tiền anh Khánh trả cho cửa hàng là 3,2 triệu đồng. Hỏi giá niêm yết của đôi giày và chiếc vợt đó là bao nhiêu triệu đồng?
Một cái cổng vòm hình parabol \(y = m{x^2}\,\,\left( {m < 0} \right)\) được thiết kế cao 6 mét, khoảng cách giữa hai chân cổng là 8 mét. Người ta muốn gắn một thanh sắt nằm ngang vào hai thành cổng để treo băng rôn (Hai đầu của thanh sắt được gắn tiếp giáp vào mặt trong của hai thành cổng). Hãy xác định hệ số \[m\] và cho biết nếu thanh sắt được gắn ở độ cao 4,5 mét so với mặt đất thì độ dài của thanh sắt là bao nhiêu mét?
Cho đường tròn \(\left( O \right)\) và dây \[BC\] không qua tâm. Điểm \[A\] di động trên cung lớn \[BC\] sao cho \(\Delta ABC\) là tam giác nhọn. Các đường cao \(AD,\,\,BE,\,\,CF\) của tam giác \[ABC\] cắt nhau ở \(H.\) Chứng minh rằng:
1) \[BCEF\] là tứ giác nội tiếp.
2) \(\frac{{BC}}{{\sin A}} = \frac{{CA}}{{\sin B}} = \frac{{AB}}{{\sin C}}\).
3) \[H\] là tâm đường tròn nội tiếp tam giác \[DEF.\]
4) Đường thẳng đi qua \[A\] và vuông góc với \[EF\] luôn đi qua một điểm cố định.
Cho các số thực dương \(a,\,\,b,\,\,c\) thỏa mãn \(a + b + c = 1.\) Chứng minh \(\frac{a}{{1 + 9\;{b^2}}} + \frac{b}{{1 + 9{c^2}}} + \frac{c}{{1 + 9{a^2}}} \ge \frac{1}{2}.\)








