Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Quảng Ninh
21 câu hỏi
I. PHẦN TRẮC NGHIỆM (3,0 điểm)
Căn bậc hai của 25 là
\(\sqrt 5 \) và \( - \sqrt 5 .\)
\( - 5\).
5.
5 và \( - 5\).
Rút gọn biểu thức\(\sqrt {64{a^2}} + 2a\) với \(a \ge 0\) ta được kết quả
\(16a.\)
\(10a\).
\(8a\).
\(6a\).
Điểm nào sau đây thuộc đồ thị hàm số \(y = 2{x^2}?\)
\(\left( {2;1} \right).\)
\(\left( {1;2} \right)\).
\(\left( {1;4} \right)\).
\(\left( {4;1} \right)\).
Các nghiệm của phương trình \(\left( {x + 2} \right)\left( {3x - 1} \right) = 0\) là
\(x = - 2\), \(x = - \frac{1}{3}.\)
\(x = - 2\), \(x = \frac{1}{3}.\)
\(x = 2\),\(x = - \frac{1}{3}.\)
\(x = 2\),\(x = \frac{1}{3}.\)
Lớp 9A có 40 học sinh, trong đó có 8 học sinh cận thị. Chọn ngẫu nhiên một học sinh của lớp, xác suất của biến cố “Học sinh được chọn không bị cận thị” là
\(\frac{1}{5}\).
\(\frac{8}{5}\).
\(\frac{4}{5}\).
\(\frac{2}{5}.\)
Nghiệm của bất phương trình \( - 2x - 4 > 0\) là
\(x > 2\).
\(x < 2\).
\(x < - 2\).
\(x > - 2\).
Đo chiều cao của học sinh lớp 9A ta có bảng tần số ghép nhóm sau:
Chiều cao (cm) | \[\left[ {150;\,\,158} \right)\] | \[\left[ {158;\,\,161} \right)\] | \[\left[ {161;\,\,164} \right)\] | \[\left[ {164;\,\,167} \right)\] |
Số học sinh | 5 | 12 | 15 | 8 |
Tần số tương đối của nhóm \[\left[ {158;\,\,161} \right)\] là
12,5%.
30%.
37,5%.
20%.
Số đo mỗi góc của một lục giác đều là
\(120^\circ \).
\(90^\circ \).
\(108^\circ \).
\(128^\circ \).
Cho hình nón có chiều cao 12 cm, bán kính đáy 5 cm. Độ dài đường sinh của hình nón đó là
12 cm.
13 cm.
11 cm.
10 cm.
Tính chiều cao của tháp canh trong hình bên (kết quả làm tròn đến hàngđơn vị). 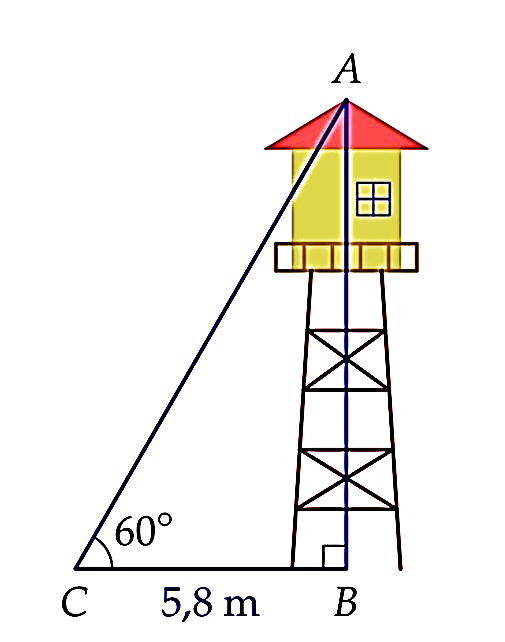
12 m.
13 m.
11 m.
10 m.
Một téc nước hình trụ có chiều cao 3 m, đường kính đáy 1 m. Thể tích nước tối đa mà téc nước chứa được là
\(\frac{1}{4}\pi \,\,({{\rm{m}}^3})\).
\(\frac{3}{4}\,\,({{\rm{m}}^3})\).
\(\frac{3}{4}\pi \,\,({{\rm{m}}^3})\).
\(\frac{4}{3}\pi \,\,({{\rm{m}}^3})\).
Cho tam giác \[ABC\] vuông tại \[A.\] Khẳng định nào sau đây là sai?
\(AB = BC.\cos B.\)
\(AC = AB.\sin B.\)
\(\tan B = \frac{{AC}}{{AB}}.\)
\(\cot B = \frac{{AB}}{{AC}}.\)
II. PHẦN TỰ LUẬN (7,0 điểm)
Rút gọn biểu thức \(\frac{1}{{\sqrt x - 2}} + \frac{1}{{\sqrt x + 2}} - \frac{x}{{x - 4}}\)với \(x \ge 0;x \ne 4\).
(0,75 điểm) Giải hệ phương trình \[\left\{ \begin{array}{l}3x - y = 9\\5x + 2y = 4.\end{array} \right.\]
(0,75 điểm) Giải bất phương trình \(\frac{{5x + 3}}{4} < \frac{{4x - 5}}{3}\).
(0,75 điểm)Giả sử phương trình \[{x^2} - 7x + 2 = 0\] có hai nghiệm là \[{x_1}\] và \({x_2}\). Không giải phương trình, hãy tính giá trị biểu thức \[\frac{{x_1^3 + x_2^3}}{{x_1^2 + 7{x_2}}}\].
(1,0 điểm)Quãng đường \(AB\) dài 200 km. Lúc 8 giờ, một xe tải đi từ \[A\] đến \(B;\) 40 phút sau, một xe con cũng đi từ \[A\] đến \[B\] với vận tốc lớn hơn vận tốc xe tải 10 km/h. Hai xe đến \[B\] cùng một lúc. Hỏi hai xe đến \[B\] lúc mấy giờ?
1) Chứng minh \[BM\] là tia phân giác của \(\widehat {ABC}.\)
2) Chứng minh \(M{E^2} = MH \cdot MB.\)
3) Đường tròn ngoại tiếp tam giác \[BEH\] cắt nửa đường tròn \(\left( O \right)\) tại \[F,\] tia \[EF\] cắt \[AB\] tại \[P,\] hai đường thẳng \[BM\] và \[AF\] cắt nhau tại \[Q.\] Chứng minh \[PQ \bot AB.\]
(0,5 điểm)Một ô tô đang chuyển động trên đường thẳng \[AC\] theo hướng từ \[A\] đi về phía \[C\] với vận tốc \[10\,\,{\rm{m/s}}\], một người đứng tại \(B\) cách mép đường một khoảng \(BH = 50\) m. Khi khoảng cách giữa người và ô tô là \(AB = 200\) m thì người đó bắt đầu chạy ra đón ô tô (coi ô tô và người chuyển động thẳng đều).Tìm vận tốc tối thiểu và hướng chạy của người tạo với \[AB\;\] góc bao nhiêu để đón được ô tô (tham khảo hình vẽ dưới đây).
![Tìm vận tốc tối thiểu và hướng chạy của người tạo với \[AB\;\] góc bao nhiêu để đón được ô tô (tham khảo hình vẽ dưới đây). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/03/26-1741766461.png)








