12 bài tập Một số bài toán hàm hợp liên quan đến tính đơn điệu và cực trị có đáp án
12 câu hỏi
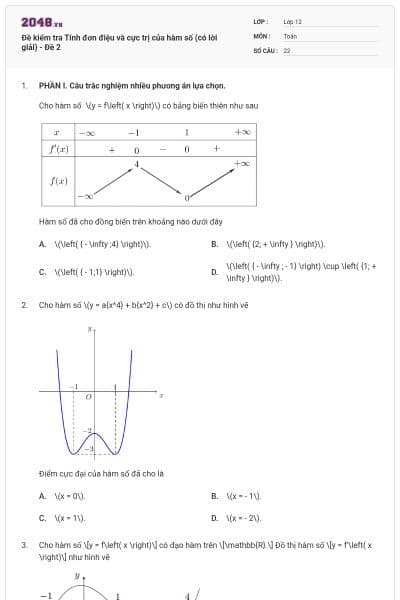
Cho hàm số f(x), bảng xét dấu của f'(x) như sau:
![]()
Tìm khoảng đồng biến của hàm số y = f(5 – 2x).
Cho hàm số y = f(x) có đạo hàm f'(x) = (x2 – 1)(x – 4) với mọi x ∈ ℝ. Hàm số g(x) = f(3 – x) có bao nhiêu điểm cực đại.
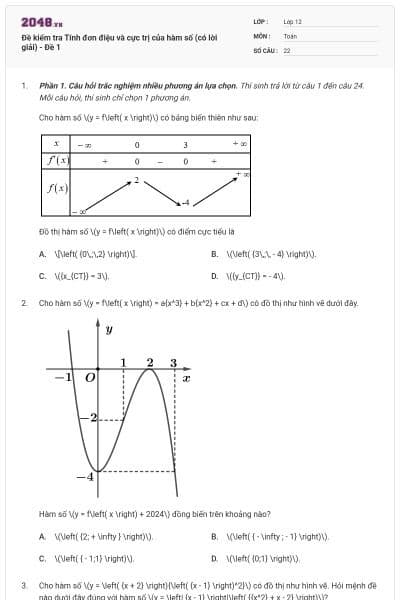
Cho hàm số y = f'(x) có đồ thị như hình vẽ
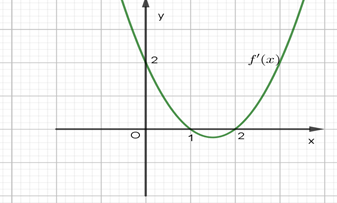
Hàm số y = f(2 – x2) đồng biến trên khoảng (a; b) khi đó a + 2b có giá trị là
1;
2;
3;
4.
Cho hàm số y = f(x) có đồ thị y = f'(x) như hình sau. Hàm số g(x) = f(3 – 2x) + 2024 đồng biến trên khoảng nào dưới đây?
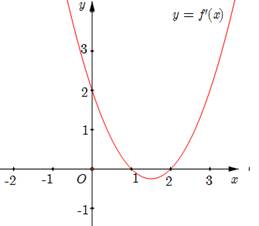
(1; +∞);
\(\left( {\frac{1}{2};1} \right)\);
\(\left( {0;\frac{1}{2}} \right)\);
\(\left( { - \infty ;\frac{1}{2}} \right)\).
Cho hàm số y = f(x) có đạo hàm trên ℝ thỏa mãn f(2) = f(−2) = 0 và đồ thị hàm số y = f'(x) có dạng như hình vẽ bên dưới.
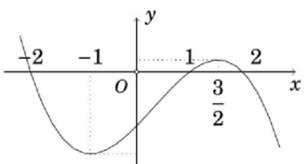
Hàm số g(x) = (f(x))2 nghịch biến trên khoảng nào dưới đây?
(−2; −1);
\(\left( { - 1;\frac{3}{2}} \right)\);
(−1; 1);
(1; 2).
Cho hàm số y = f(x) có đạo hàm f'(x) = x2(x – 9)(x – 4)2. Khi đó hàm số g(x) = f(x2) đồng biến trên khoảng nào?
(−2; 2);
(3; +∞);
(−∞; −3);
(−∞; −3) ∪ (0; 3).
Cho hàm số y = f(x) = ax4 + bx3 + cx2 + dx + e, đồ thị hình bên là đồ thị của hàm số y = f'(x).
Xét hàm số g(x) = f(x2 – 2) . Mệnh đề nào dưới đây sai?
Hàm số g(x) nghịch biến trên khoảng (−∞; −2);
Hàm số g(x) đồng biến trên khoảng (2; +∞);
Hàm số g(x) nghịch biến trên khoảng (−1; 0);
Hàm số g(x) nghịch biến trên khoảng (0; 2).
Cho hàm số y = f'(x) có đồ thị như hình bên. Tìm số điểm cực trị của hàm số g(x) = f(x2 – 2x) trên khoảng (0; +∞).
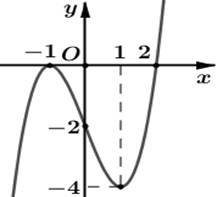
3;
2;
4;
1.
Cho hàm số y = f(x) có đạo hàm f'(x2 – 1)(x – 4) với mọi x ∈ ℝ. Hàm số g(x) = f(3 – x) có bao nhiêu điểm cực đại?
0;
1;
2;
3.
Cho hàm số y = f(x) có đạo hàm liên tục trên ℝ, bảng biến thiên của hàm số f'(x) như sau:
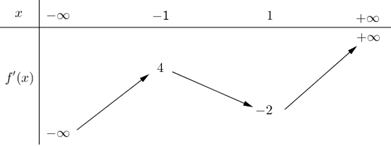
Số điểm cực trị của hàm số y = f(x2 + 2x) là
4;
5;
1;
7.
Cho hàm số y = f(x) xác định, liên tục trên ℝ và có đúng hai điểm cực trị x = −1; x = 1có đồ thị như hình vẽ sau:
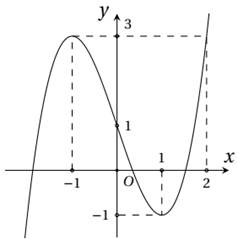
Hỏi hàm số y = f(x2 – 2x + 1) có bao nhiêu điểm cực trị?
4;
3;
1;
2.
Cho hàm số y = f(x) có bảng biến thiên như hình dưới:
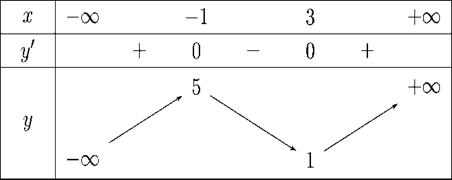
Số điểm cực trị của hàm số y = f(x2 – 4x + 1)là:
3;
2;
1;
5.