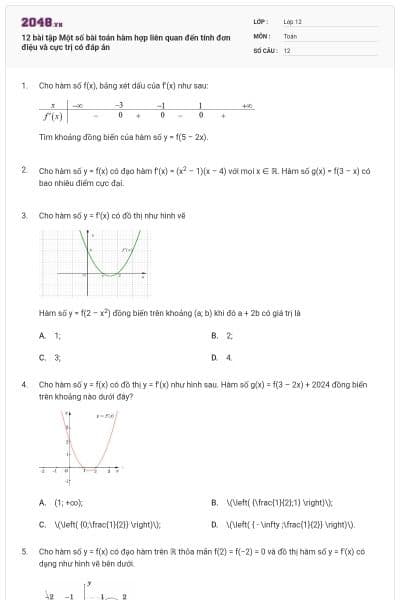
12 bài tập Một số bài toán liên quan đến tính đơn điệu, cực trị có chứa tham số có đáp án
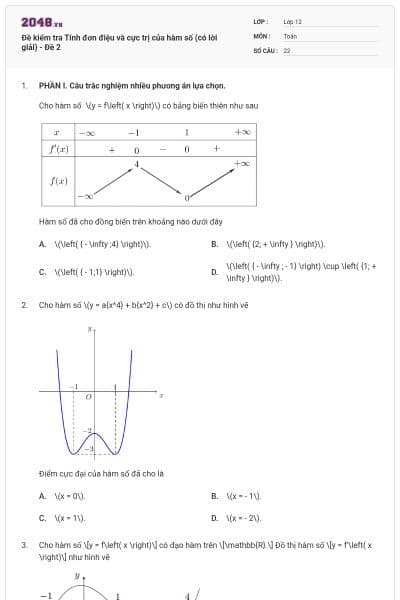
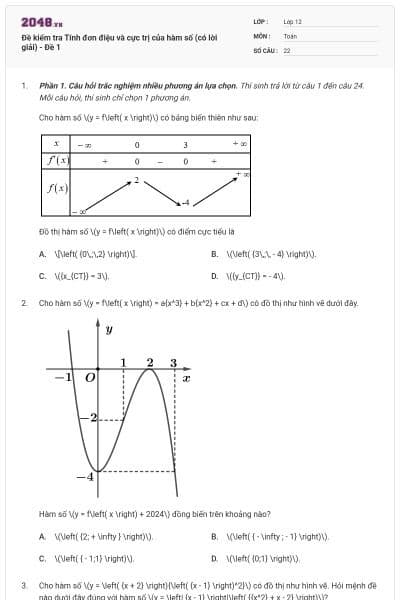
12 câu hỏi
Tổng các giá trị nguyên của tham số m ∈ [−10; 10) để hàm số y = x3 − 3x2 +3(m + 2)x + 3m – 2025 đồng biến trên trên ℝ là:
27;
35;
44;
54.
Biết giá trị tham số \(m \in \left[ {a;\frac{b}{c}} \right]\) (với a, b, c ∈ ℤ và \(\frac{b}{c}\) là phân số tối giản) thì hàm số y = x3 – (2m – 1)x2 + (2 – m)x + 2 đồng biến trên trên ℝ. Giá trị biểu thức \(P = \frac{{{a^2} + {b^2}}}{c}.\)
\(P = \frac{9}{4}\);
\(P = \frac{{13}}{2}\);
P = 4;
\(P = \frac{{13}}{4}\).
Tập hợp tất cả các giá trị thực của tham số m để hàm số y = x3 – 3x2 + (4 – m)x đồng biến trên khoảng (2; +∞) là
(−∞; 1];
(−∞; 4];
(−∞; 1);
(−∞; 4).
Có bao nhiêu giá trị nguyên âm của tham số m để hàm số \(y = \frac{{ - 3}}{4}{x^4} + \frac{9}{2}{x^2} - \left( {2m + 15} \right)x - m + 3\) nghịch biến trên khoảng (0; +∞)?
2;
3;
4;
5.
Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = \frac{{x + {m^2}}}{{x + 4}}\) đồng biến trên từng khoảng xác định của nó
2;
3;
4;
5.
Với giá trị tham số m ∈ (a; b)\{c} (với a, b, c ∈ ℤ) thì hàm số y = (m + 2)x3 + 3x2 + mx – 6 có 2 cực trị. Giá trị biểu thức P = a + b + c là:
P = −4;
P = 4;
P = −3;
P = −5.
Có bao nhiêu giá trị nguyên âm của tham số m ∈ [−2020; 2020) để hàm số y = mx3 + 3mx2 – (m – 1)x – 1 có cực trị?
2038;
2020;
2018;
2021.
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x4 – 12x2 + (m – 2)x có ba điểm cực trị?
47;
44;
46;
45.
Biết rằng hàm số y = (x + a)3 + (x + b)3 – x3 có hai điểm cực trị. Mệnh đề nào sau đây là đúng?
ab ≤ 0;
ab < 0;
>
ab > 0;
ab ≥ 0.
Tìm tất cả các giá trị của tham số thực m để hàm số y = mx3 − 2mx2 + (m – 2)x + 1 không có cực trị
m ∈ (−∞; 6) ∪ (0; +∞);
m ∈ (−6; 0);
m ∈ [−6; 0);
m ∈ [−6; 0].
Tìm m để hàm số \(f(x) = \frac{1}{3}{x^3} + m{x^2} + 4x + 3\) đồng biến trên ℝ.
Tất cả các giá trị thực của tham số m để hàm số \(y = \frac{{{x^5}}}{5} - \frac{{m{x^4}}}{4} + 2\) đạt cực đại tại x = 0.